【数据结构与算法】归并排序

概念

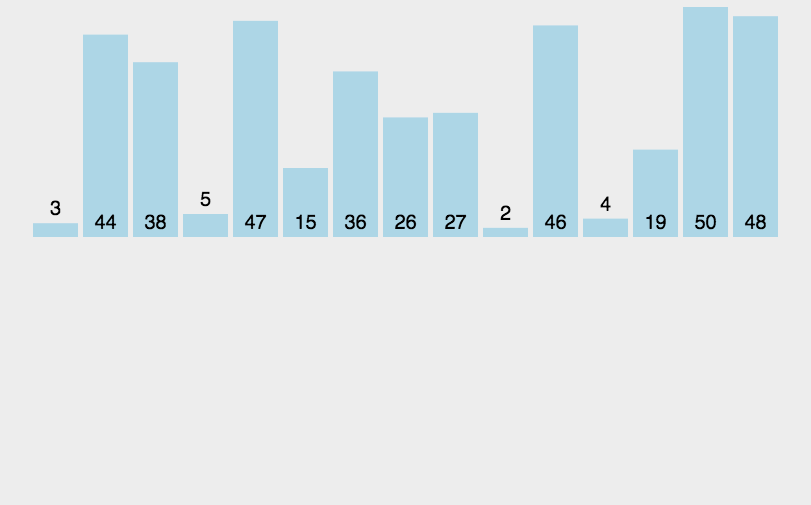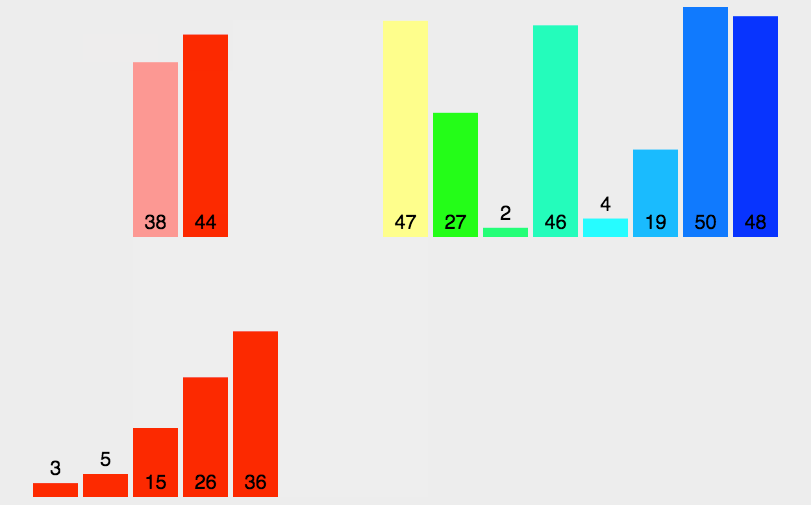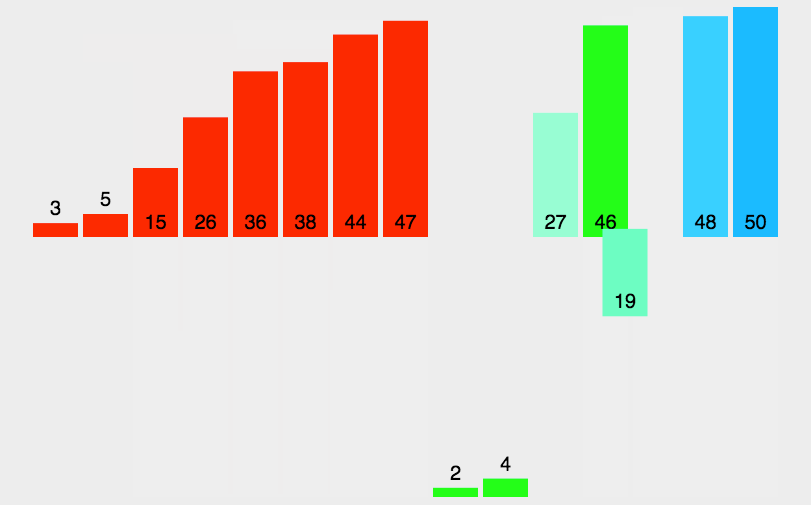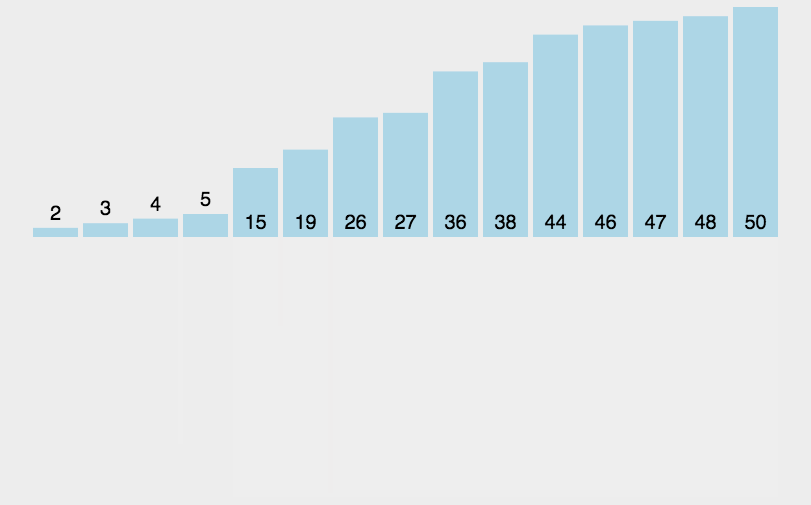
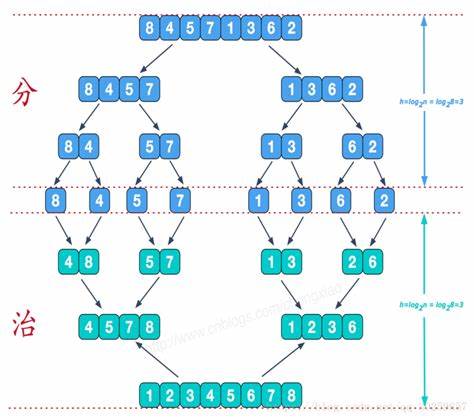
过程

• 分解：将n 个元素分成个含n/2 个元素的子序列；
• 解决：对两个子序列递归地排序
• 合并：合并两个已排序的子序列以得到排序结果

和快排不同的是

• 归并的分解较为随意
• 重点是合并
• 需要额外开辟数组空间

代码实现

    public static void mergeSort(int[] arr){
        if(arr == null||arr.length<2) return; //数组元素至少为2
        mergeSort(arr,0,arr.length-1);
    }
    public static void mergeSort(int[] arr,int L, int R){
        if(L == R) return;  //递归边界
        int mid =  L+((R - L) >> 1);  //注意这里的移位运算的括号不能少
        mergeSort(arr,L,mid);   //左侧数组归并排序
        mergeSort(arr, mid+1, R);   //右侧数组归并排序
        merge(arr, L, mid, R);
    }
    public static void merge(int[] arr, int L, int m, int R){
        int[] help = new int[R-L+1];  //辅助数组
        int i = 0;  //辅助数组下标
        int p1 = L;  //第一个待合并数组起点
        int p2 = m + 1;  //第二个待合并数组起点
        while(p1 <= m && p2 <= R){  //排好的部分拷贝到辅助数组
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }
        while(p1 <= m){  //继续处理剩下的数组
            help[i++] = arr[p1++];
        }
        while(p2 <= R){  //继续处理剩下的数组
            help[i++] = arr[p2++];
        }
        for (int j = 0; j < help.length; j++) {  //拷贝回原数组
            arr[L + j]=help[j];
        }
    }

复杂度分析

套用master公式T(N) = a*T(N/b) + O(N^d)
a=2，b=2，d=1
log(b,a) = d -> 时间复杂度为O(N^d * logN) =O(NlogN)
额外空间复杂度 O(N)

所以：

• 时间复杂度：O(NlogN)
• 空间复杂度：O(N)
• 稳定性：稳定
• 非原址排序

经典例题

剑指 Offer 51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:
输入: [7,5,6,4]
输出: 5
 
限制：
0 <= 数组长度 <= 50000

在一次合并过程中：

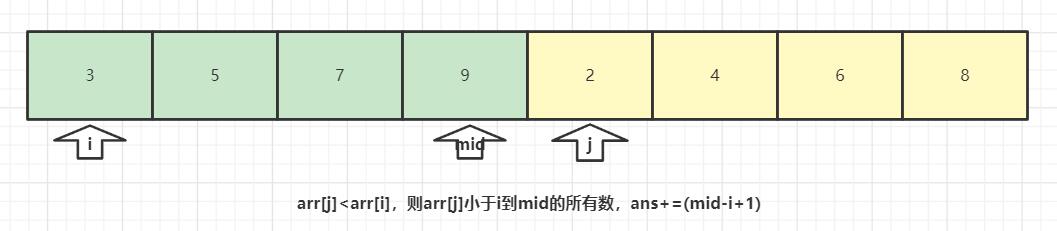
稍微修改一下归并排序代码即可

	class Solution {
        private int ans = 0;     //声明实例变量
        public int reversePairs(int[] nums) {
            mergeSort(nums, 0, nums.length - 1);
            return ans;
        }
        public void mergeSort(int[] arr, int low, int high) {
            if (arr.length < 2 || low >= high) return;
            int mid = low + ((high - low) >> 1);
            mergeSort(arr, low, mid);
            mergeSort(arr, mid + 1, high);
            merge(arr, low, mid, high);
        }
        public void merge(int[] arr, int low, int mid, int high) {
            int[] helper = new int[high - low + 1];
            int i = low;
            int j = mid + 1;
            int k = 0;
            while (i <= mid && j <= high) {
                if (arr[i] <= arr[j]) {
                    helper[k++] = arr[i++];
                } else {
                    ans += mid - i + 1;   //注意：如果arr[i]>arr[j]则i~mid这个区间的所有数都大于arr[j],因为[low……mid]和[mid+1……high]是已经排好序的。
                    helper[k++] = arr[j++];
                }
            }
            while (i <= mid) {
                helper[k++] = arr[i++];
            }
            while (j <= high) {
                helper[k++] = arr[j++];
            }
            for (int m = 0; m < helper.length; m++) {
                arr[low + m] = helper[m];
            }
        }
    }