【数据结构与算法】位运算

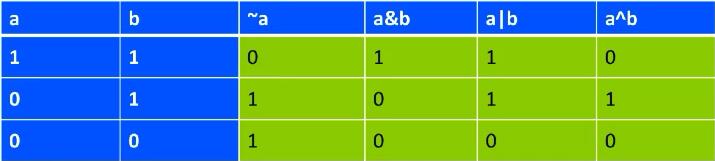
位运算符

& ：与
| ：或
^ ：异或
~ ：非（取反）
>> << ：右移（补符号位），左移（补0）
>>> ：右移（0补充高位）
对于int型，1<<35与1<<3是相同的，而左边的操作数是long型时需要对右侧操作数模64

异或：
可以理解为不进位加法：1+1=0，0+0=0，1+0=1
性质：
1、交换律：a ^ b = b ^ a
2、结合律：(a ^ b) ^ c = a ^ (b ^ c)
3、对于任何数x，都有x ^ x = 0，x ^ 0 = x
4、自反性：a ^ b ^ b = a ^ 0 = a，连续和同一个因子做异或运算，最终结果为自己

应用

判断奇偶数

x & 1 = 1 x是奇数
x & 1 = 0 x是偶数

核心是判断二进制数最后一位是1还是0

交换两个整数变量的值

使用前提：a，b不相等

a = a^b;
b = a^b;
a = a^b;

不用判断语句求整数绝对值

(num^(num>>31))+(num>>>31)

11111111 11111111 11111111 11110111：num
11111111 11111111 11111111 11111111：num>>31
00000000 00000000 00000000 00001000：num^(num>>31)
00000000 00000000 00000000 00000001：num>>>31
00000000 00000000 00000000 00001001：num^(num>>31))+(num>>>31

正数显然满足
负数的相反数是原码含符号位取反加一

消除最低位的1

x&(x-1) ：可以使二进制数x的最低位的1变成0；

例题

找出唯一成对的数

1-1000这1000个数放在含有1001个元素的数组中，只有唯一的一个元素值重复，其它均只出现一次。每个数组元素只能访问一次，设计一个算法，将它找出来;不用辅助存储空间，能否设计一个算法实现?

核心：x^x=0

可以强行配凑消去其他元素：这1001个元素连续异或，再异或上1-1000这1000个数。
其他元素都出现2次，异或后变成0.而唯一的一个元素值出现3次，连续异或后值不变。

public static void main(String[] args) {
        int []arr = new int[]{1,2,3,4,4,5};
        int ans = 0;
        for(int i=1;i<=5;i++){
            ans^=i;
        }
        for(int i=0;i<6;i++){
            ans^=arr[i];
        }
        System.out.println(ans);
}

找出落单的数

一个数组里除了某一个数字之外，其他的数字都出现了两次。请写程序找出这个只出现一次的数字。

public static void main(String[] args) {
        int []arr = new int[]{1,1,3,4,4};
        int ans = 0;
        for(int i=0;i<arr.length;i++){
            ans^=arr[i];
        }
        System.out.println(ans);
}

二进制中1的个数

请实现一个函数，输入一个整数，输出该整数二进制表示中1的个数。
例：9的二进制表示为1001，有2位是1

法一：
该二进制数不断无符号右移并与1做与运算，结果为1则count++，直到该数变为0

public static void main(String[] args) {
        int n=-1;
        int count = 0;
        while (n!=0){
            int tmp = n&1;
            if(tmp == 1) count++;
            n = n >>> 1 ;
        }
        System.out.println(count);
    }   //32

法二：
每次使该二进制数的一个为1的二进制位变成0，count++，直到该数变成0；
x&(x-1) ：可以使二进制数的最低位的1变成0；

public static void main(String[] args) {
        int n=-1;
        int count = 0;
        while (n!=0){
            n = n&(n-1);
            count++;
        }
        System.out.println(count);
    }

是不是2的整数次方

用一条语句判断一个整数是不是2的整数次方

也就是一个整数的二进制形式中为1的二进制位是不是只有一个。联系上一题，也就是count是不是为1

public static void main(String[] args) {
        int n=65536;
        System.out.println((n&(n-1))==0);
}

整数的二进制奇偶位交换

先取出偶数位和奇数位，偶数结果右移一位，奇数结果左移一位，最后异或
abababab abababab abababab abababab
a0a0a0a0 a0a0a0a0 a0a0a0a0 a0a0a0a0（ou）
0b0b0b0b 0b0b0b0b 0b0b0b0b 0b0b0b0b（ji）
0a0a0a0a 0a0a0a0a 0a0a0a0a 0a0a0a0a（ou>>>1）
b0b0b0b0 b0b0b0b0 b0b0b0b0 b0b0b0b0（ji<<1)
babababa babababa babababa babababa

public static void main(String[] args) {
    int a = 0b01000000_00000000_00000000_00000000;
    System.out.println(a);
    int b = m(a);
    System.out.println(b);  //0b10000000_00000000_00000000_00000000
  }

  private static int m(int i) {
    int ou = i & 0xaaaaaaaa;//和1010 1010 1010 。。。。做与运算取出偶数位
    int ji = i & 0x55555555;//和0101 0101 0101 。。。。做与运算取出奇数位
    return (ou >>> 1) ^ (ji << 1); // 连起来
  }

0~1直接的浮点实数的二进制表示

给定一个介于0和1之间的实数，（如0.625)，类型为double,打印它的二进制表示(0.101，因为小数点后的二进制分别表示0.5,0.25.0.125......) 。
如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”

public static void main(String[] args) {
    double num = 0.625;
    StringBuilder sb = new StringBuilder("0.");
    while (num > 0) {
      //乘2：挪整
      double r = num * 2;
      //判断整数部分
      if (r >= 1) {
        sb.append("1");
        //消掉整数部分
        num = r - 1;
      } else {
        sb.append("0");
        num = r;
      }

      if (sb.length() > 34) {
        System.out.println("ERROR");
        return;
      }

    }
    System.out.println(sb.toString());
  }

出现k次与出现1次

数组中只有一个数出现了1次，其他的数都出现了k次，请输出只出现了1次的数。

2个相同的2进制数做不进位加法，结果为0
10个相同的10进制数做不进位加法,结果为O
k个相同的k进制数做不进位加法，结果为0

public static void main(String[] args) {
    int[] arr = {2, 2, 2, 9, 7, 7, 7, 3, 3, 3, 6, 6, 6, 0, 0, 0};
    int len = arr.length;
    char[][] kRadix = new char[len][];
    int k = 3;

    int maxLen = 0;
    //转成k进制字符数组
    //对于每个数字
    for (int i = 0; i < len; i++) {
      //求每个数字的k进制字符串并翻转，然后转为字符数组
      kRadix[i] = new StringBuilder(Integer.toString(arr[i], k)).reverse().toString().toCharArray();
      if (kRadix[i].length > maxLen)
        maxLen = kRadix[i].length;
    }
    //不进位加法
    int[] resArr = new int[maxLen];
    for (int i = 0; i < len; i++) {
      //  不进位加法
      for (int j = 0; j < maxLen; j++) {
        if (j >= kRadix[i].length)
          resArr[j] += 0;
        else
          resArr[j] += (kRadix[i][j] - '0');
      }
    }

    int res = 0;
    for (int i = 0; i < maxLen; i++) {
      res += (resArr[i] % k) * (int) (Math.pow(k, i));// 8%3=2,
    }
    System.out.println(res);
  }

出现奇数次的两种数

在一组数中，有两种数出现了奇数次，其他类型的数出现了偶数次，问这两个出现奇数次的数是什么，时间复杂度小于O(N)

解析：设这两个数是a和b，所以所有数字第一次连续异或可以得到a^b。下面我们只需要想办法搞出a或者b。
举个例子，我们成功搞出a来，那么异或运算a^ba就可以得到b。注意到a和b前提是肯定不相同，那么在二进制的层面看这两个数字，它们肯定至少有一位数字是不一样的，一个是0，一个是1
a:…………0001…………
b:…………0000…………
下面要做的就是把所有出现了两次的数字根据ab这一位不同的数字进行分组。
这一位数字为0的数字为一组，这一位数字为1的数字为一组

让其中一组进行连续异或，比如这一位为1的这一组数字连续异或，出现偶数次的数字异或为0，最后只剩下a，我们就成功得到了a。
最后进行a ^ b ^ a就可以得到b
本题默认寻找a，b从右到左第一次出现的不同二进制位的位置，这也是本题的关键，等价于求ab异或后从右向左第一次出现1的位置。
记住一个公式：原码和补码做与运算可以得到二进制数从右到左第一次出现1的位置为1，其他位置为0的数

	1010111100
&	0101000100
=	0000000100

    public static void printOddTimesNum2(int[] arr) {
		int eO = 0, eOhasOne = 0;
		for (int curNum : arr) {
			eO ^= curNum;
		}
		int rightOne = eO & (~eO + 1);  原码和补码做与运算
		for (int cur : arr) {
			if ((cur & rightOne) == 1) { 该位是1的为一组
				eOhasOne ^= cur;
			}
		}
		System.out.println(eOhasOne + " " + (eO ^ eOhasOne));
	}