【数据结构与算法】简单排序(选择、冒泡、插入、希尔排序)、二分查找
选择排序
概念
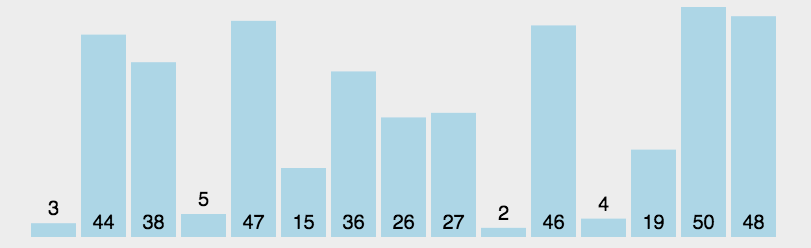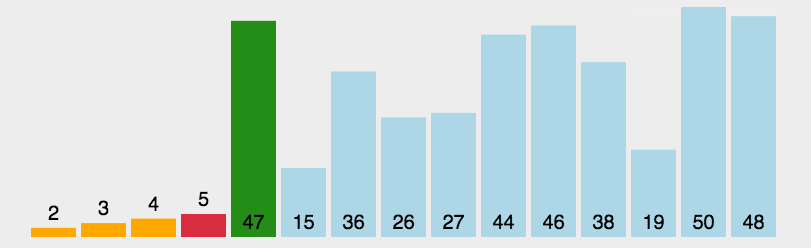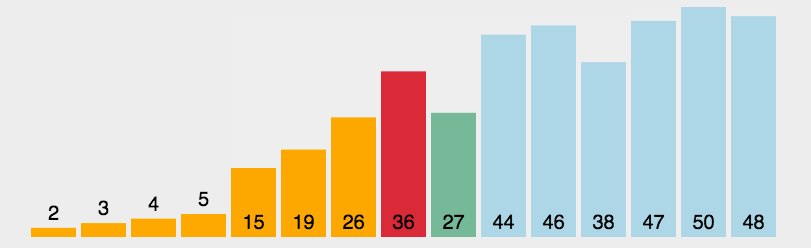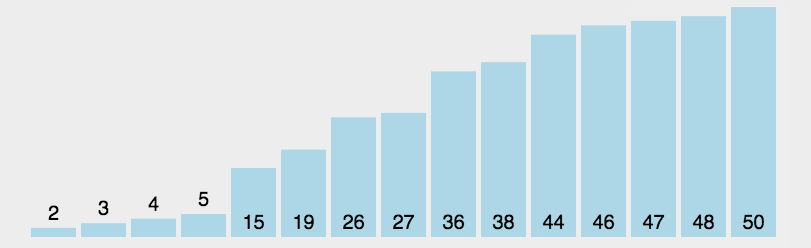
首先,找到数组中最小的那个元素,其次,把它和数组的第一个元素交换位置(如果第一个元素就是最小的元素那么它就和自己交换)。再次,在剩下的元素中找到最小的元素,将它与数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种方法叫做选择排序,因为它在不断地选择剩余元素中地最小者。
代码实现
public static void SelectionSort(int[] arr){
if(arr==null||arr.length<2) return; //去除多余情况
int N = arr.length;
for (int i = 0; i < N-1; i++) {
int minIndex = i;
for (int j = i+1; j < N; j++){
if(arr[j] < arr[minIndex]) minIndex = j; //更新每一轮最小元素的下标
}
swap(arr,i,minIndex);
}
}
public static void swap(int[] arr, int i, int j){ //交换元素
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
改进:二元选择排序
public static void selectionSort2(int[] arr) {
int minIndex, maxIndex;
// i 只需要遍历一半
for (int i = 0; i < arr.length / 2; i++) {
minIndex = i;
maxIndex = i;
for (int j = i + 1; j < arr.length - i; j++) {
if (arr[minIndex] > arr[j]) {
// 记录最小值的下标
minIndex = j;
}
if (arr[maxIndex] < arr[j]) {
// 记录最大值的下标
maxIndex = j;
}
}
// 如果 minIndex 和 maxIndex 都相等,那么他们必定都等于 i,且后面的所有数字都与 arr[i] 相等,此时已经排序完成
if (minIndex == maxIndex) break;
// 将最小元素交换至首位
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
// 如果最大值的下标刚好是 i,由于 arr[i] 和 arr[minIndex] 已经交换了,所以这里要更新 maxIndex 的值。
if (maxIndex == i) maxIndex = minIndex;
// 将最大元素交换至末尾
int lastIndex = arr.length - 1 - i;
temp = arr[lastIndex];
arr[lastIndex] = arr[maxIndex];
arr[maxIndex] = temp;
}
}
复杂度分析
选择排序过程中,0~N-1 上任意位置i都要进行一次交换和N-1-i次比较。因此总共有N次交换和(N-1)+(N-2)+……+1=N(N-1)/2~N^2/2次比较。
也就是O(N^2)
- 不稳定排序
冒泡排序
概念
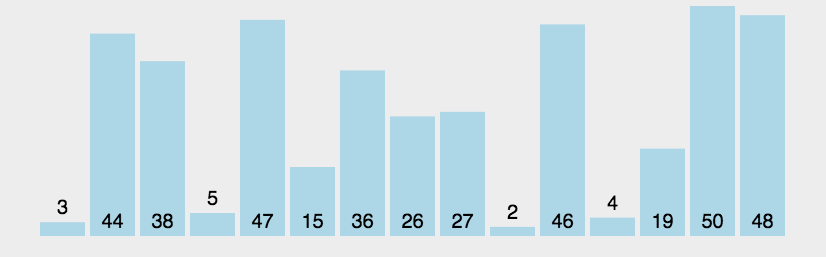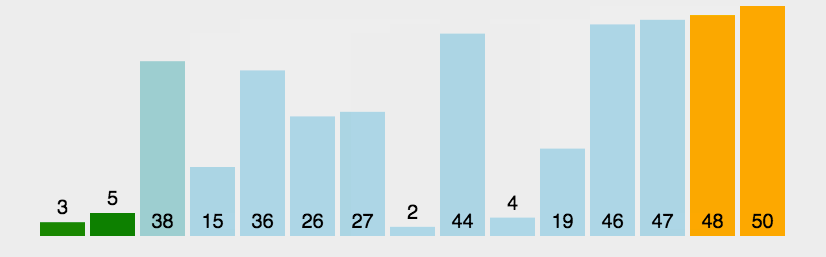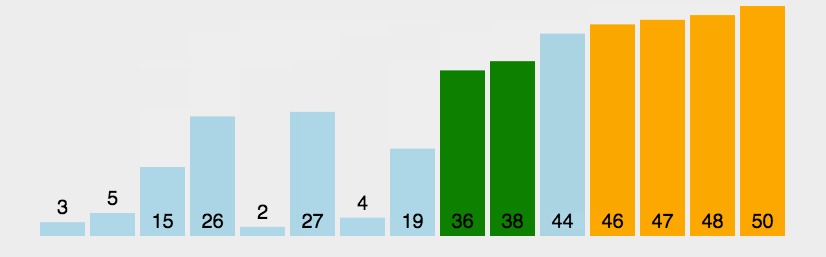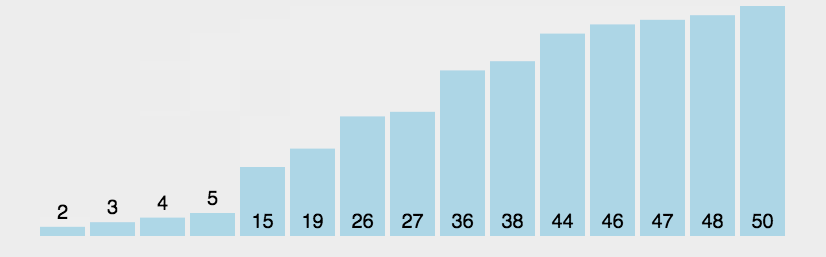
从第一个元素开始遍历数组每两个元素一组比较,如果不满足从小到大的排序规则则进行交换,这样最后可以得到最大元素在数组最后的位置排好。如此往复,直到整个数组排好。
代码实现
法一:
循环每经过一轮,剩余数字中的最大值仍然是被移动到当前轮次的最后一位
public static void sort(int[] arr){
if(arr==null||arr.length<2) return; //去除多余情况
for(int i = arr.length - 1; i >= 0;i--){ //外层反向遍历
for(int j = 0;j < i; j++){
if(arr[j] > arr[j+1])
swap(arr,j,j+1);
}
}
}
public static void swap(int[] arr, int i, int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
法二:flag标记
如果一轮比较中没有发生过交换,则立即停止排序,因为此时剩余数字一定已经有序了。
public static void sort2(int[] arr) {
boolean flag = true;
for (int i = arr.length - 1; i >= 0; i--) {
if (!flag) break;
flag = false;
for (int j = 0; j < i; j++) {
if (arr[j + 1] < arr[j]) {
swap(arr, j, j + 1);
flag = true;
}
}
}
}
复杂度分析
总的比较次数是(N-1)+(N-2)+……+1=N(N-1)/2~N^2/2
也就是O(N^2)
- 稳定排序
插入排序
概念
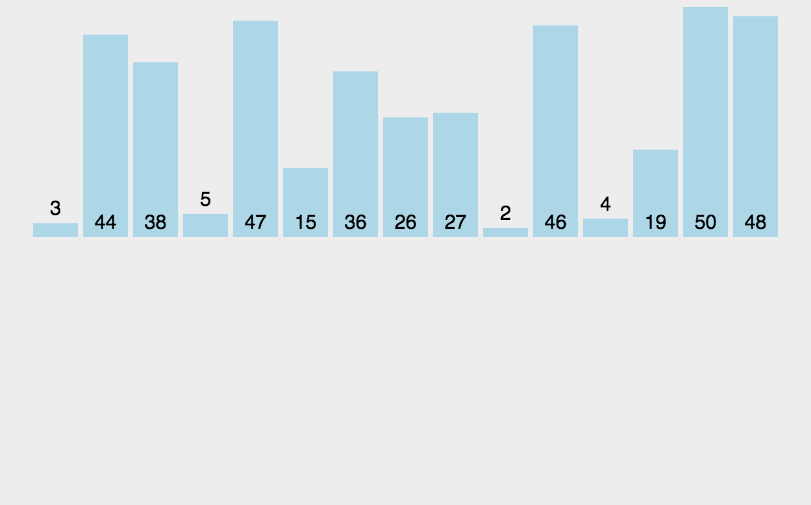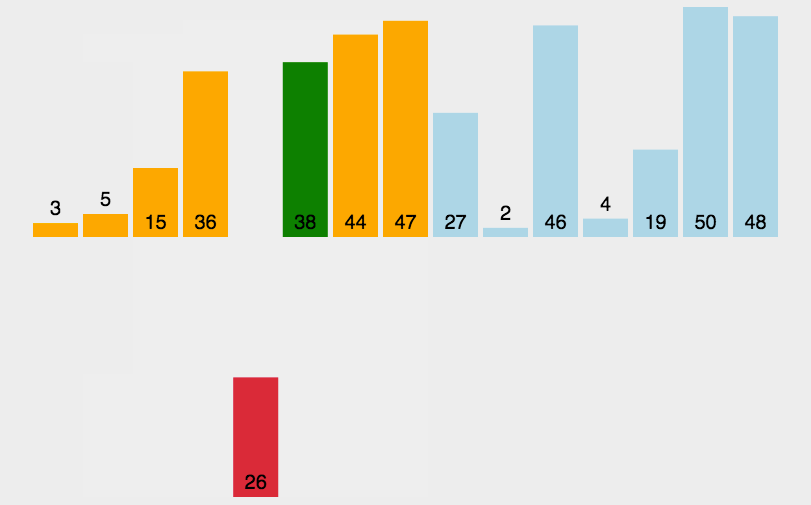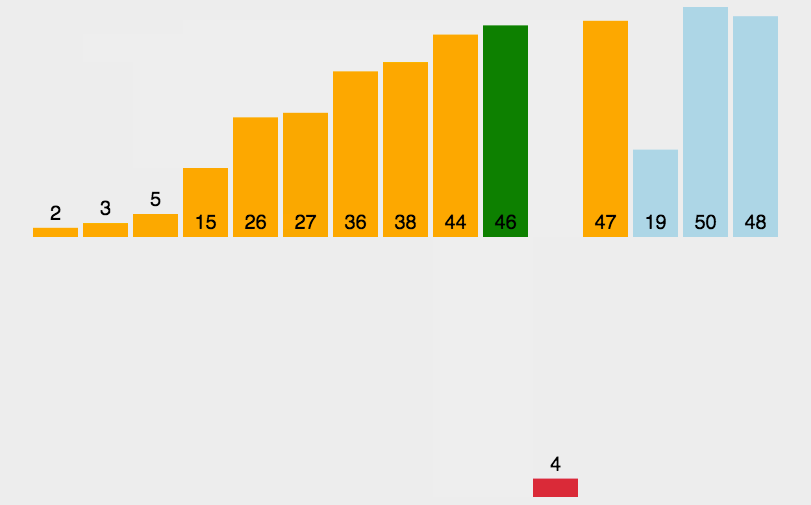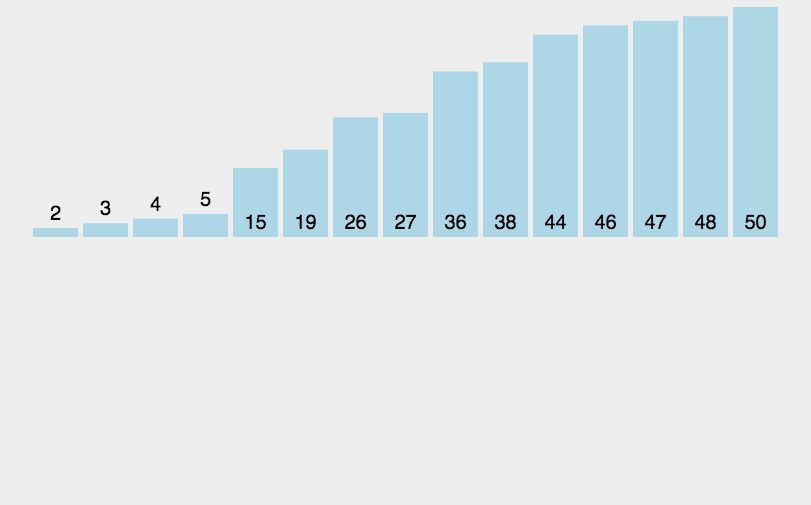
从左向右遍历,每次把遍历到的元素放到前面已经排好顺序的数组的合适位置。如此往复,直到整个数组排好。
代码实现
public static void sort(int[] arr){
if(arr==null||arr.length<2) return; //去除无效情况
for(int i = 1; i < arr.length; i++){ //i从1开始,认为i为1时已经排好
for(int j = i-1; j >= 0 && arr[j] > arr[j+1]; j--)
swap(arr,j,j+1);
}
}
public static void swap(int[] arr, int i, int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
复杂度分析
总的比较和交换次数都是(N-1)+(N-2)+……+1=N(N-1)/2~N^2/2
也就是O(N^2)
- 稳定排序
希尔排序
概念
希尔排序是插入排序的一种。
也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法
-
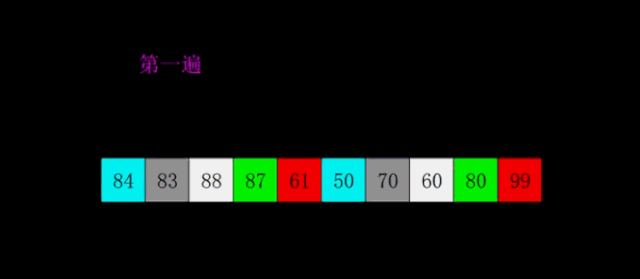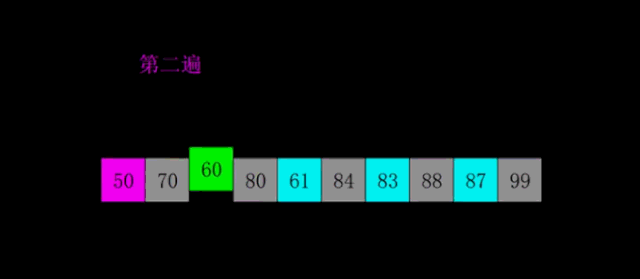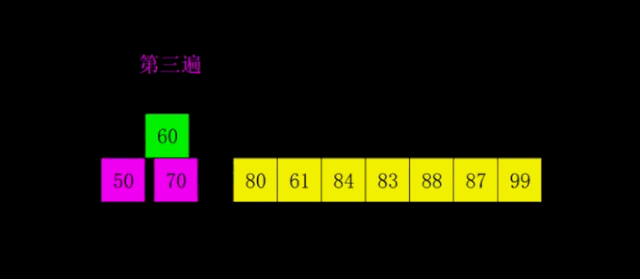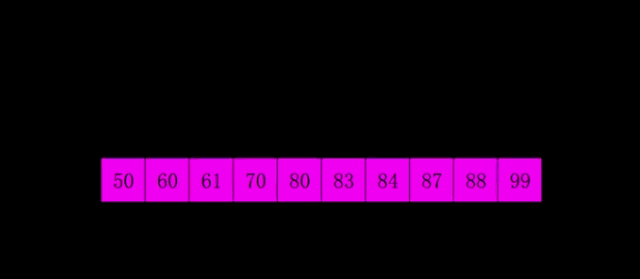
思路:如序列 9 8 7 6 5 4 3 2 1
确定一个增量序列,如 4(length/2) 2 1 ,从大到小使用增量
使用第一个增量,将序列划分为若干个子序列,下标组合为0-4-8,1-5,2-6,3-7
依次对子序列使用直接插入排序法;
使用第二个增量,将序列划分为若干个子序列(0-2-4-6-8),(1-3-5-7)
依次对子序列使用直接插入排序法:
使用第三个增量1,这时子序列就是元序列(0-1-2-3-4-5-6-7-8),使用直接插入法完成排序。 -
时间复杂度:不太确定在O(nlogn)~O(n²)之间
-
空间复杂度:O(1)
-
原址排序
-
稳定性:由于相同的元素可能会被划分至不同子序列单独排序,因此稳定性是无法保证的——不稳定
代码实现
public static void main(String[] args) {
int[] arr = {9, 9, 6, 7, 5, 4, 2, 2, 1};
shellSort(arr);
for(int i = 0; i < arr.length; i++){
System.out.println(arr[i]+" ");
}
}
public static void shellSort(int[] arr) {
//不断地缩小增量
for (int interval = arr.length / 2; interval > 0; interval = interval / 2) {
//增量为interval的插入排序
for (int i = interval; i < arr.length; i++) {
int target = arr[i]; //使用target临时变量保存arr[i]
int j = i - interval; //j 指向缩小增量数组的i 元素的前一个元素下标
while (j >= 0 && target < arr[j]) {
arr[j + interval] = arr[j];
j -= interval;
}
arr[j + interval] = target;
}
}
}
时间性能分析
希尔排序开始时增量较大,每个子序列中的记录个数较少,从而排序速度较快;当增量较小时,虽然每个子序列中记录个数较多,但整个序列已基本有序,排序速度也较快。
希尔排序算法的时间性能取决于增量的函数,而到目前为止尚未有人求得一种最好的增量序列。研究表明,希尔排序的时间性能在O(n^2)和O(nlogn)之间。当n在某个特定范围内,希尔排序所需的比较次数和记录的移动次数约为O(n ^1.3)。
二分查找
左侧边界二分查找
-
如果数组中有目标值,在arr上,找满足=value的最左位置
-
如果数组中没有目标值,返回大于value的第一个数的位置
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
public static int binarySearch(int[] nums, int target) {
int n = nums.length;
int l = 0;
int r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
return nums[l] == target ? l : -1;
}
右侧边界二分查找
-
如果数组中有目标值,在arr上,找满足=value的最右位置
-
如果数组中没有目标值,返回小于value的第一个数的位置
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
public static int binarySearch(int[] nums, int target) {
int n = nums.length;
int l = 0;
int r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (nums[mid] <= target) l = mid;
else r = mid - 1;
}
return nums[l] == target ? l : -1;
}
整数二分总结
- 左侧边界二分查找
先写if (arr[mid] >= value) - 右侧边界二分查找
先写if (arr[mid] <= value) - 别忘了最后对index为-1做特殊处理,防止数组越界访问
浮点数二分
手动开方
public static double sqrt(double x) {
double l = 0, r = x;
while (r - l > 1e-8) {
double mid = (l + r) / 2;
if (mid * mid >= x)
r = mid;
else
l = mid;
}
return r;
}


