离散数学（图与网络）

图

图的基本概念

简单图：不允许有平行边和反身边。

无向图：允许有平行边和反身边。

有限图：有限点构成的图一定是有限图，但是有限边构成的图不一定是有限图（可能有无数个孤立点）

零图：只有点，没有边。

完全图：任意两点之间都有边。边的数量是\(\mathrm{C}_{\mathrm{m}}^{2}\) （m是顶点数）

图的同构：图经过一系列物理变化（伸缩、旋转），变化前后的两个图看成同一个图

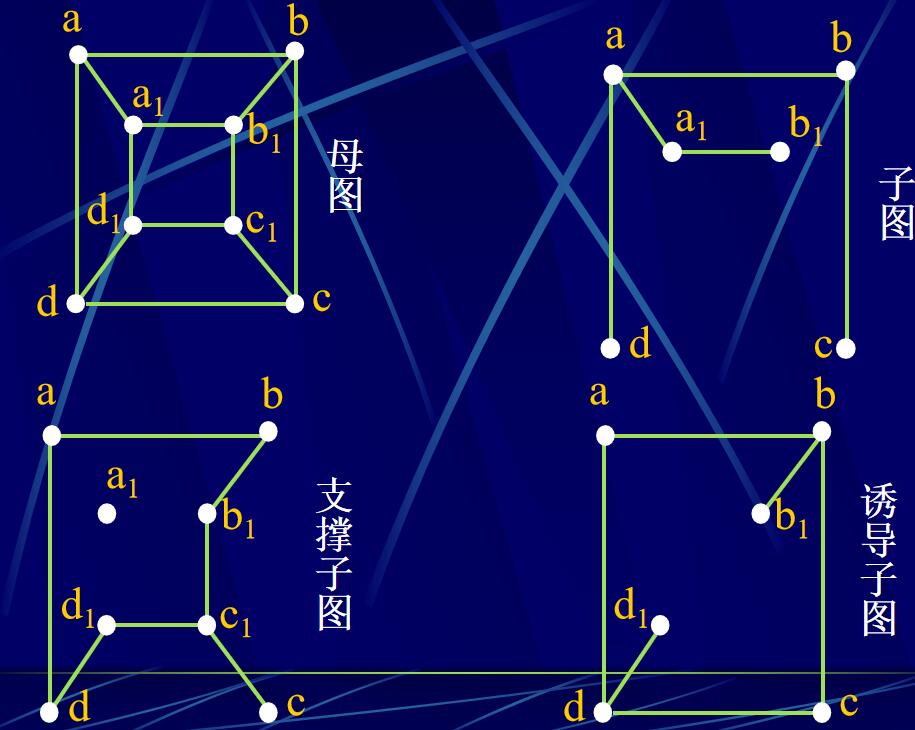
母图

子图：母图的一部分

支撑子图：点与母图一致，边可以少

诱导子图：去点母图某个（些）点的同时把与点相连的边去掉。

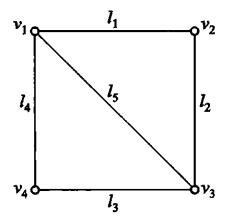
度：\(d_G\left( v \right)\)与某点相连的边的个数。 度为0的点为“孤立点”

关联矩阵：表示点和边之间的关系

特点：

1. 每一列之和一定为2，因为每一条边一定只有两个顶点

2. 每一行之和表示该顶点的度，因为表示它是某一个边的顶点

\[\begin{matrix}{} l1& l2& l3& l4& l5\\ \end{matrix} \\ \begin{array}{} v1\\ v2\\ v3\\ v4\\ \end{array}\left( \begin{matrix}{} 1& 0& 0& 1& 1\\ 1& 1& 0& 0& 0\\ 0& 1& 1& 0& 1\\ 0& 0& 1& 1& 0\\ \end{matrix} \right) \]

邻接矩阵：表示点与点之间有没有边

特点：

1. 主对角线元素为0
2. 对称矩阵
3. 每一行或每一列之和表示顶点的度

\[\,\, \begin{matrix}{} v1& v2& v3& v4\\ \end{matrix} \\ \begin{array}{} v1\\ v2\\ v3\\ v4\\ \end{array}\left( \begin{matrix}{} 0& 1& 1& 1\\ 1& 0& 1& 0\\ 1& 1& 0& 1\\ 1& 0& 1& 0\\ \end{matrix} \right) \]

定理4.1.1：所有点的度数之和是边数的二倍（所有点的度数之和一定是偶数)

\[\sum_{v\in P\left( G \right)}{d_{G\left( v \right) =2m}} \]

定理4.1.2：在任一有限图中，奇数点的个数为偶数

证明：由定理4.1.1，且知道偶数点的度之和一定是偶数，那么奇数点的度数之和一定也是偶数，那么奇数点的个数也一定是偶数

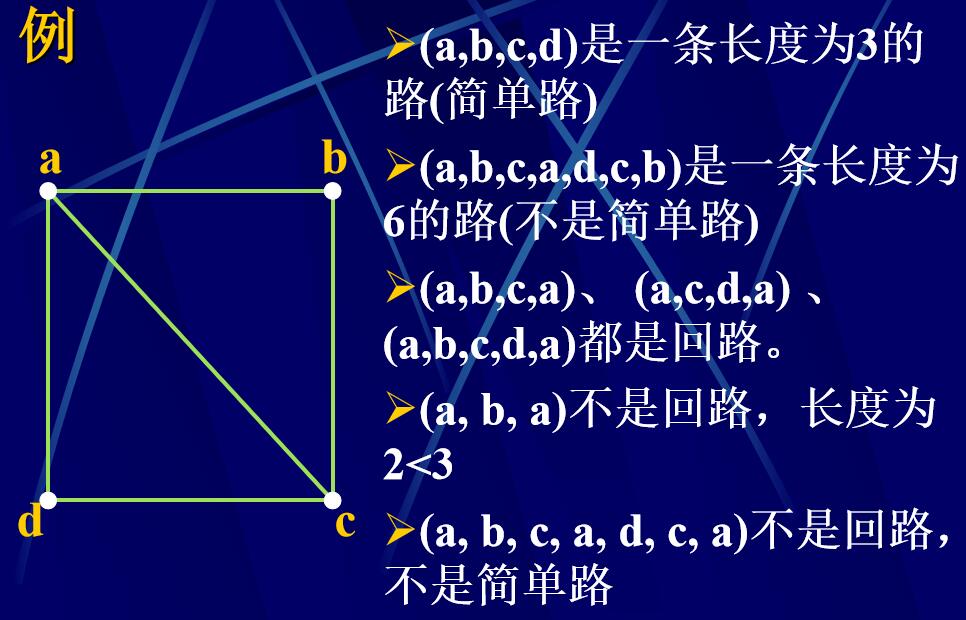
简单路：除开头v0和结尾点vn可以相同以外，路径上的点不可以相同

回路：G中从点v到自身的长度不小于3的简单路

相连：从u到v有一条路（v与自身相连）

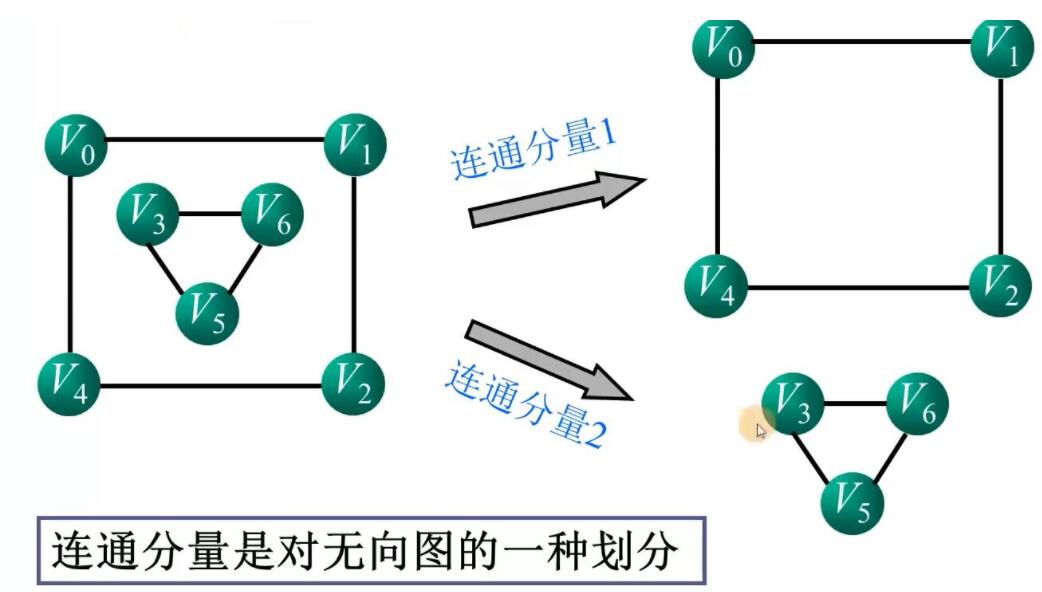
连通分支：非连通图的极大连通子图

证明一个图是连通图的方法：

1.直接证明

2.反证法

常考定理：设G=(P，L)是有限图，P(G)，L(G)的元数分别为m，n。证明：如果n> \(\mathrm{C}_{\mathrm{m}-1}^{2}\) ，则G是连通的。（至少m-1个点之间都有边）

证明：反证法。假设此时G不是连通的，则将G中的一个连通分支作为一个子图记为G1，剩余的部分记为G2。可设P(G1)的元数为m1，P(G2) 的元数为m2，其中1≤m1，m2<m，m1+m2=m。则：

n≤m1(m1-1)/2+ m2(m2-1)/2=1/2(\(\mathrm{m1}^2\)+\( \mathrm{m2}^2 \)- m1- m2)
=1/2( \( \mathrm{(m1+m2)}^2\)- 2m1m2 - （ m1+ m2 ）)
=1/2(\(\mathrm{m}^2\)-m-2m1m2)

由于(m1-1) (m2-1) ≥0所以有：
m1 m2- (m1+m2)+1≥0 即 m1 m2≥ m-1，则有：
n≤1/2(\(\mathrm{m}^2\)-m-2m1m2)≤1/2(m2-m-2(m-1))
=1/2(m2-3m+2)=1/2(m-1)(m-2)= \(\mathrm{C}_{\mathrm{m}-1}^{2}\)

例题：有限图G，|P(G)|=6，|L(G)|=11，则G可能不是连通图（X）

解：\( \mathrm{L}\left( \mathrm{G} \right) =11>\mathrm{C}_{5}^{2}=10\) 一定连通

权图 Dijkstra算法（单源点最短路径问题）

权值：带有某种含义的边

最短路径：两顶点之间经历的权值之和最短的路径

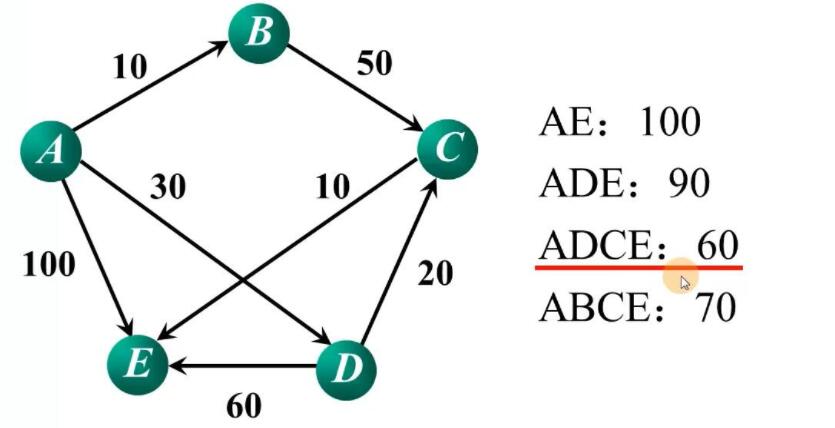
Dijkstra算法

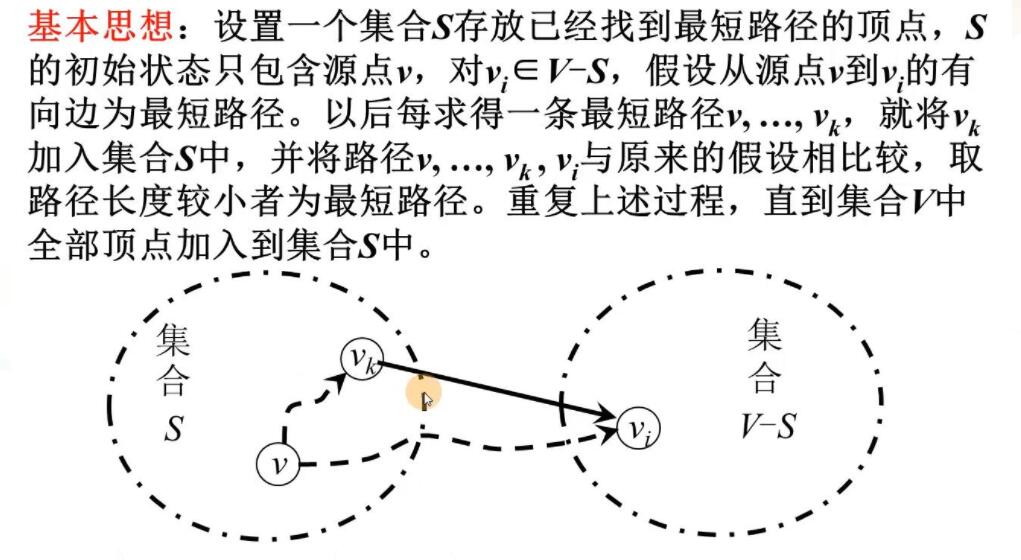
Dijkstra算法演示

例一

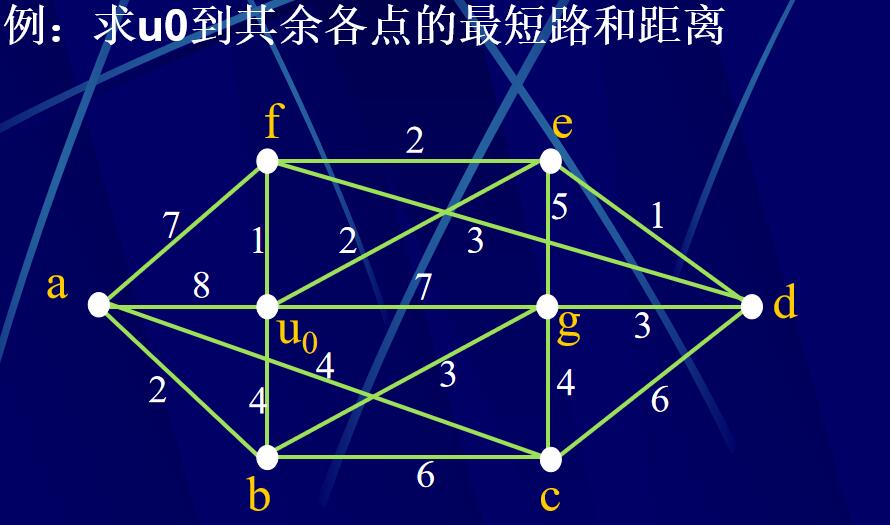
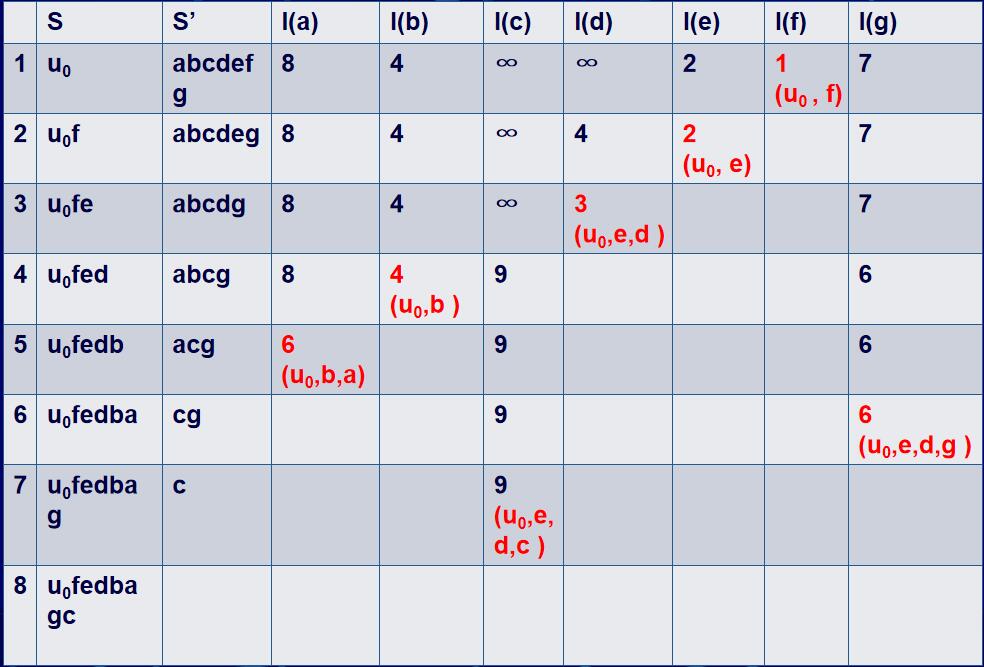
例二

首先确定是一个邻接矩阵，可以画出权图，求A到其他点的最短路径

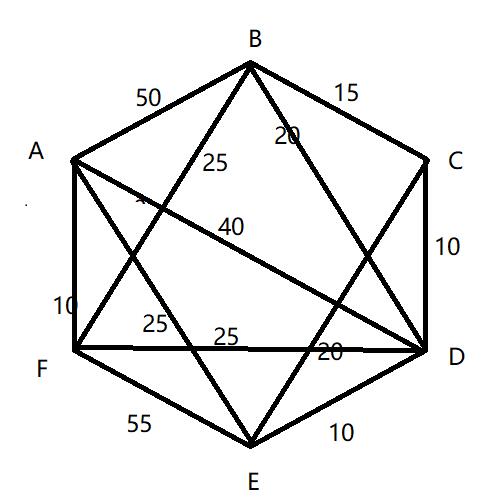
列表：

S	S'	B	C	D	E	F
A	BCDEF	50	\(\infty\)	40	25	10(AF)
AF	BCDE	35(AFB)	\(\infty\)	35(AFD)	25(AE)
AFE	BCD	35(AFB)	45(AEC)	35(AFD)(AED)
AFEB	CD		45(AEC)	35(AFD)(AED)
AFEBD	C		45(AEC)(AFDC)(AEDC)
AFEBDC

第一轮：

l(B)=w(AB)=50,l(C)=w(AC)= \(\infty\) ,l(D)=w(AD)=40,l(E)=w(AE)=25,l(F)=w(AF)=10

第二轮：

l(B)=min{l(B),l(F)+w(FB)}=min{50,10+25}=35

l(C)=min{l(C),l(F)+w(FC)}=min{ \(\infty\) , \(\infty\) }= \(\infty\)

l(D)=min{l(D),l(F)+w(FD)}=min{40,10+25}=35

l(E)=min{l(E),l(F)+w(FE)}=min{25,10+55}=25

第三轮：

l(B)=min{l(B),l(E)+w(EB)}=min{35,25+ \(\infty\) }=35

l(C)=min{l(C),l(E)+w(EC)}=min{ \(\infty\) ,25+20}=45

l(D)=min{l(D),l(E)=w(ED)}=min{35,25+10}=35

第四轮：

l(C)=min{l(C),l(B)+w(BC)}=min{45,35+15}=45

l(D)=min{l(D),l(B)+w(BD)}=min{35,35+20}=35

第五轮：

l(C)=min{l(C),l(D)+w(DC)}=min{45,35+10}=45

​

A==>B：35(AFB)

A==>C：45(AEC)(AFDC)(AEDC)

A==>D：35(AFD)(AED)

A==>E：25(AE)

A==>F：10(AF)

树

树及其等价定义

定义4.2.1：设G=(P,L)是图，如果G是连通的，并且无回路，则称G为树．无回路的图(可能不连通)也称为森林.

引理4.2.1：设G是至少有一条边的有限图，且无回路，则G至少有一个点只相邻于另一个点，即G至少有一个点度数为1.

定理4.2.1：如果G是图，则下列诸命题等价.

(1）G是树.
(2）G连通并且删去G的任意一边，所得到的图都不连通.
(3）对G中任意两点v，v'(v≠v')，恰有一条从v到v'的简单路.

如果G还是有限图，设P(G)元数为n，则下列命题也与上面的命题等价.

(4）C不含回路，并且G有n -1条边.
(5）G连通，并且G有n -1条边.

推论4.2.1：任意有限连通图必有一支撑子图是树。今后，此支撑子图称为母图的支撑树.
推论4.2.2：若G'是有限图G的支撑树，w'为G中一边，且 w'不在G'中，则G'添上边'后必有回路.

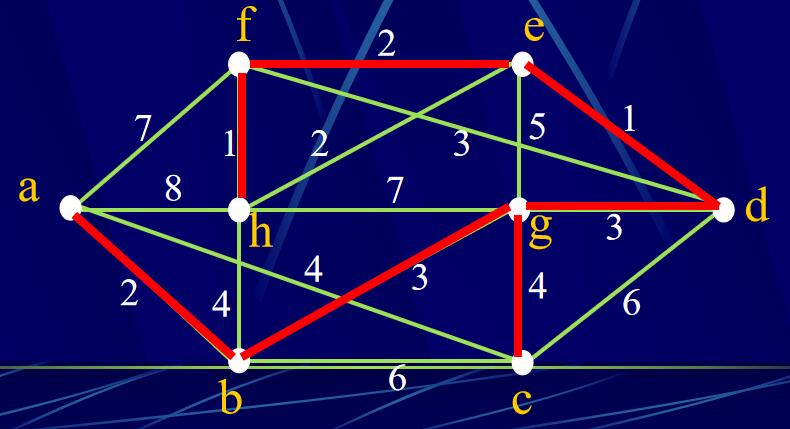
Kruskal算法

定义4.2.2：设G是加权连通图，带有最小权(和)的支撑树称为权图G的最优树。

设权图G=(P, L)是连通的。
在L(G)中选一个具有最小权值的边,记为\(l_1\),令T={ \(l_1\) }；
从L(G)-T中取\(l_i\)，使得T∪{\(l_i\)}不产生回路，并且w(\(l_i\))最小。如果存在这样的\(l_i\)，则令T= T∪ {\(l_i\)}，重复步骤2)；
如果不存在这样的\(l_i\)，则算法停止。

白话：每次选取权值最小的边，前提是不能产生回路，如果产生回路需要换一条次小的回路，......直到选出n-1条边（n是点的个数）。

树的常用结论：

1.每一株恰好有两个点度是1的树必是一条简单路(d=2(n-1))

2.若G为∆≥k的树，其中∆是G中点的最大度，则G最少有k个点的度是1(d=2(n-1))

有向图 Euler路

有向图

定义4.3.1 :G=(P, A)称为有向图，如果P是点集合，A是从一点引到一点(不要求一定是另一点)的弧集合。当P为有限集时，G称为有限有向图.若e是一条从点v到点v’的弧，则称v为e的起点，记为v=init(e)；v’为e的终点，记为v’=fin(e).
起点和终点都是点v的弧称为反身弧。

出度（输出次数）、入度（输入次数）、度（输入加输出）

有向子图（P(H) \(\subseteq\)P(G)，A(H)\(\subseteq\)A(G)）、支撑子图（P(H)=P(G))

有向路

简单有向路（简单路）：有向图的有向路，n条弧的起点互不相同，n条弧的终点也互不相同

有向回路：从点v到自身的简单有向路（长度可以为1或2）称为有向回路，是简单路。

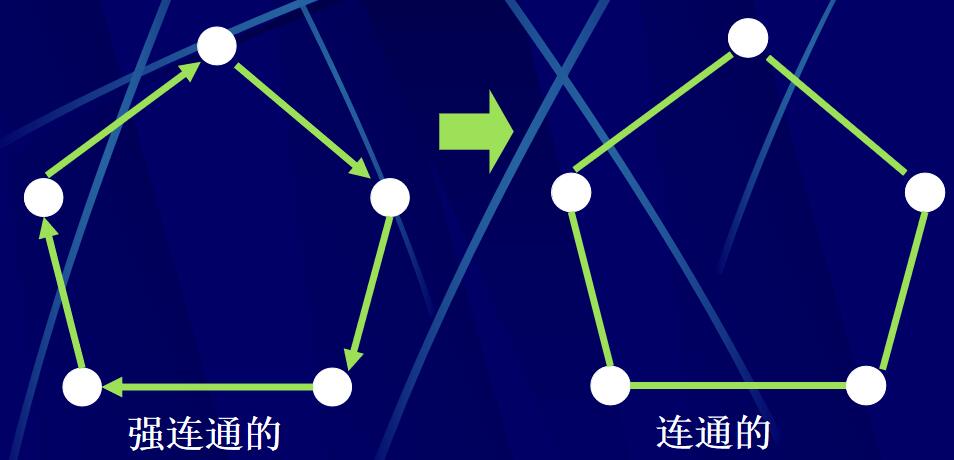
强连通：设G=(P，A)是有向图，对G中任意两点v，v’ (v\(\ne\)v’)，如果都有从v到v’的有向路，则称G是强连通的。有从任意点到任意点的路）

根：设G=(P，A)是有向图，r\(\in\)P(G)。称r为G的根，如果对G中任一点v (v\(\ne\)r)，都有从v到r的有向路。(所有点有到根的路)

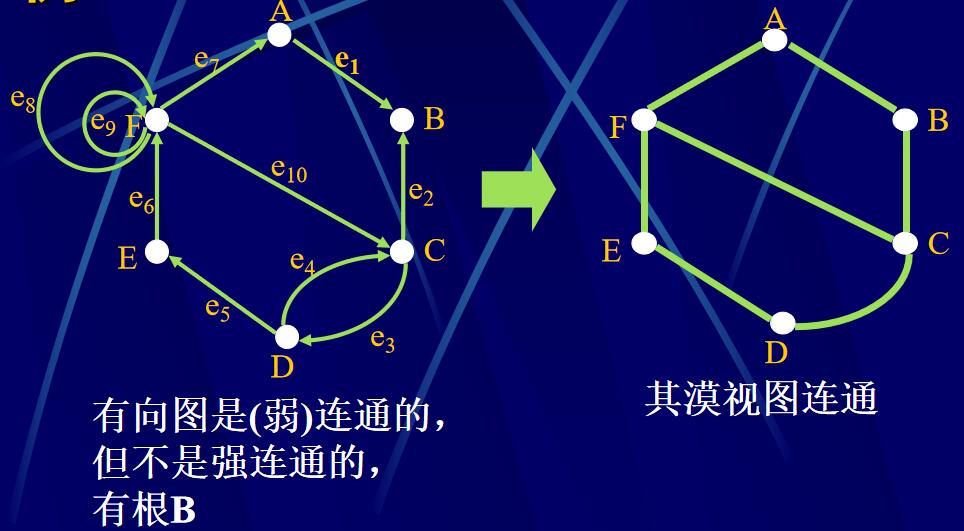
漠视图：

(1)删去G中自身到自身的弧（反身弧）；
(2)G中任意两点，若有弧，只保留一条；
(3)删去弧的方向，即得\(\mathrm{G}_0\)。

弱连通：漠视图连通。

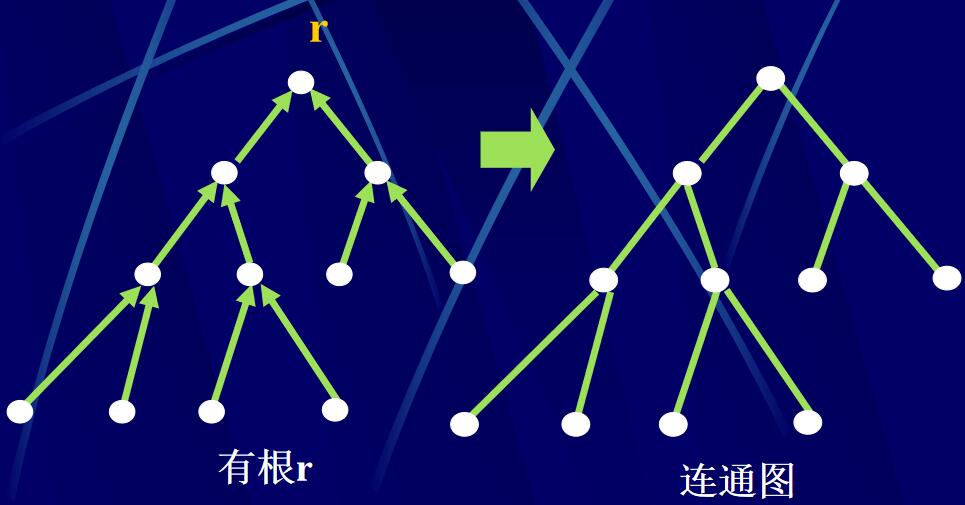
有向树：

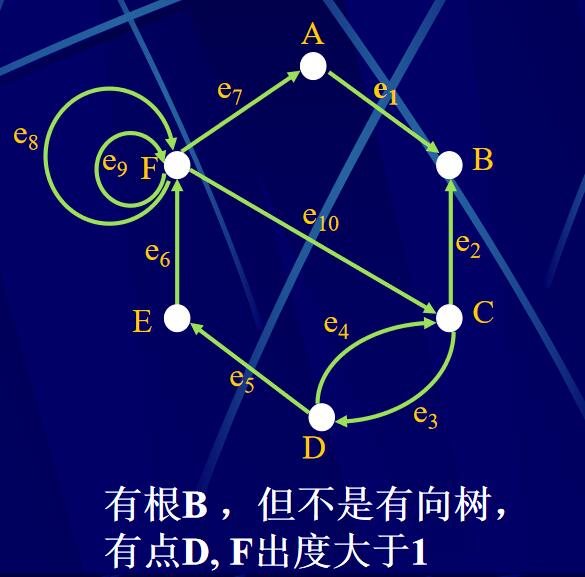
有向图G称为有向树（或有根树），如果G中有一点r，并且满足：

(1) G中每一点v(v\(\ne\)r）都恰是一条弧e的起点;

(2) r不是任一条弧的起点;

(3) r是根。

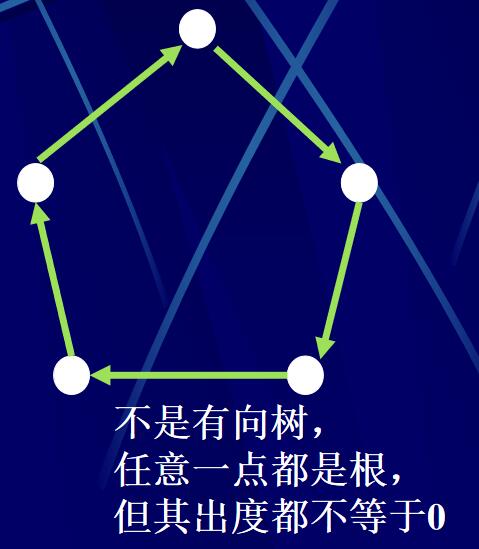
有向树的特点：

1. 每一点v(v\(\ne\)r)到r恰有一条有向路；
2. 没有有向回路；
3. 两点间最多有一条弧。

转化定理：

对有向树G，若无视各弧之方向,则得一树\(\mathrm{G}_0\)； (--命题1)
反之，若\(\mathrm{G}_0\)是树，可选取任一点做根，并适当指定各边之方向，则得一有向树G。（--命题2）

Euler路

Euler路：（注意这个图很重要）

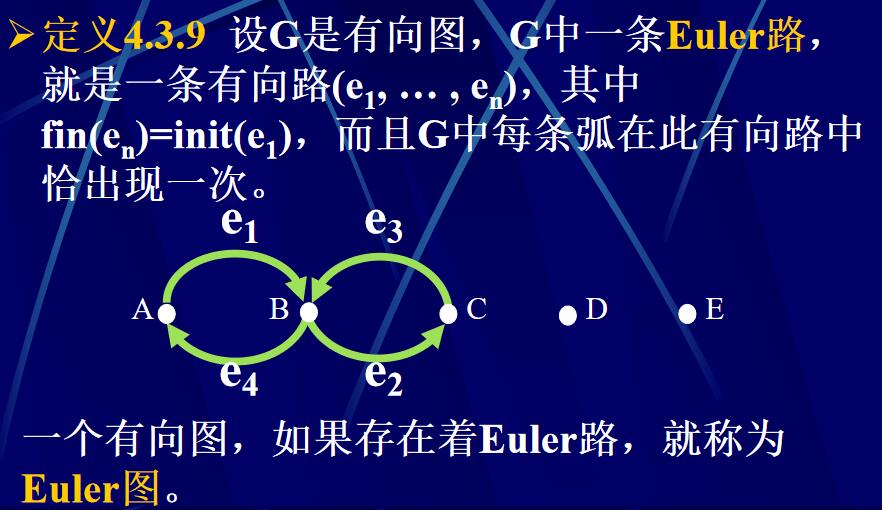
Euler路实际上是一条封闭的一笔画路线

平衡有向图：设G是有向图。如果G中每点v，都有有限的输入次数和输出次数，而且输入次数和输出次数相等。

一有限平衡有向图，其弧数必有限。
一有向图若存在Euler路，则必平衡。

判定Euler图的充要条件：设G是无孤立点的有限有向图。于是，G有Euler路当且仅当G是平衡的，并且强连通。

推论：设G是无孤立点的有限有向图，于是，G有Euler路当且仅当G平衡，并且将G漠视为图\(\mathrm{G}_0\)时是连通的（弱连通） 。

哈密顿（Hamilton）图

Hamilton路 Hamilton图的必要条件

定义4.4.1 设G=(P, L)是有限图，(v1, … , vn)是G中一条路。如果G中每点恰在此路中出现一次，则称此路为Hamilton路。
如果G中每点，除v1外，恰在此路中出现一次，而v1=vn，则此路称为Hamilton回路。

定义4.4.2 设G=(P, L)是有限图，如果G中有一条Hamilton回路，则称G为Hamilton图。

比较Hamilton路、Hamilton回路与Euler路：

Hamilton路一定为简单路；
Euler路未必简单有向路。
Hamilton路着眼于无重复地遍历图中诸点；
Euler路着眼于无重复地遍历有向图中诸弧。
Hamilton路、Hamilton回路是G的支撑子图,
Hamilton路是G的支撑树；
Euler路未必为G的支撑子图。
存在Euler路，未必存在 Hamilton回路。
存在Hamilton回路，未必存在Euler路。

Hamilton路和Hamilton回路的性质

1. 若图中有一点的度为1，则无Hamilton回路。
2. 若图中有一点的度为0，则既无Hamilton路，
   又无Hamilton回路。
3. 设图中有一点的度为2，若有Hamilton回路，
   则以此点为端点的两条边均出现在此回路中。
4. 设图中有一点的度大于2，若有Hamilton回
   路，则只用其中的两条边。
5. 若图中有n个点，则
   Hamilton路恰有n-1条边，
   Hamilton 回路恰有n条边。
6. Hamilton路是图G的支撑子树，
   Hamilton回路是图G的支撑子图。

Hamilton路、Hamilton图的必要条件

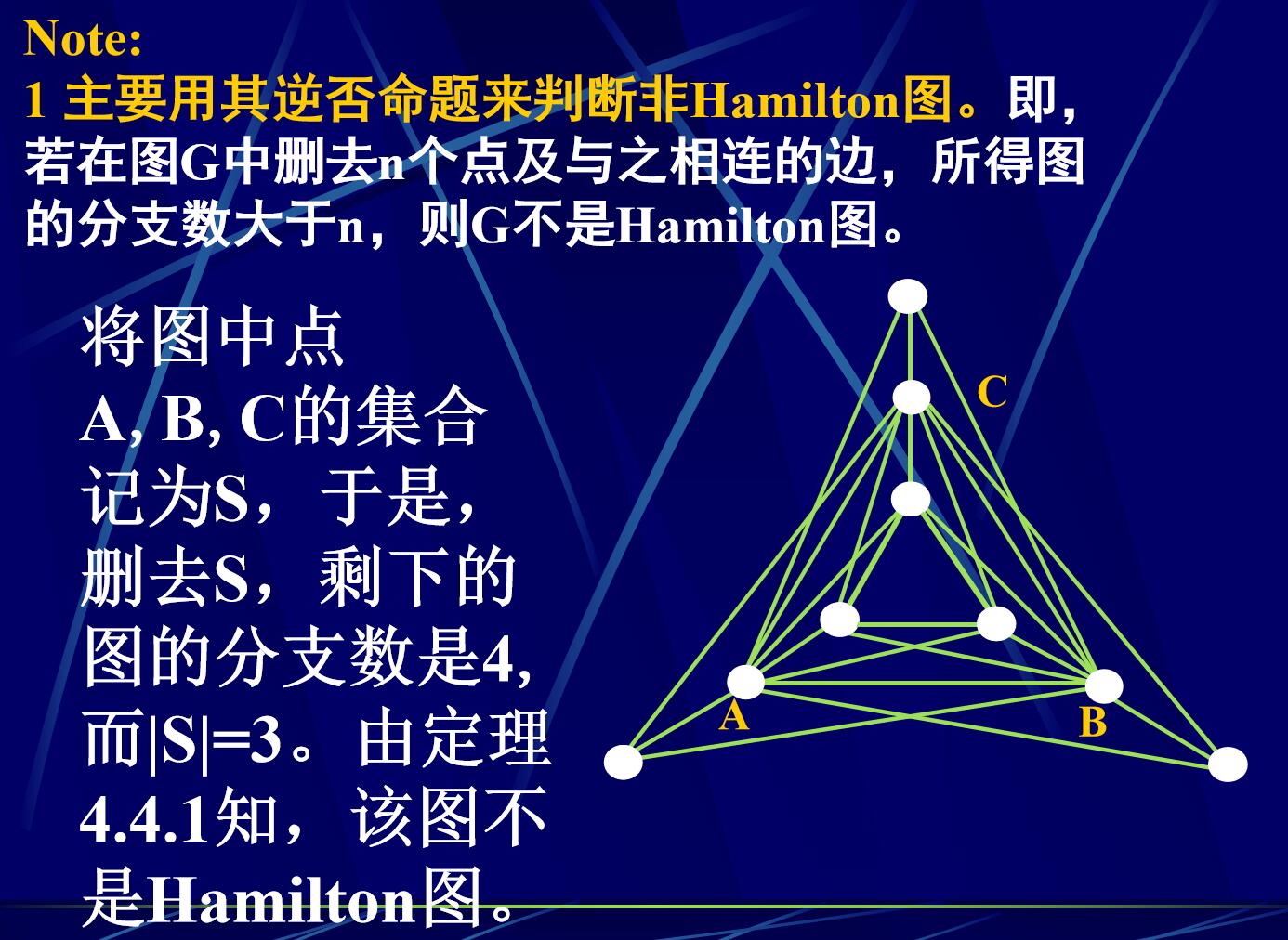
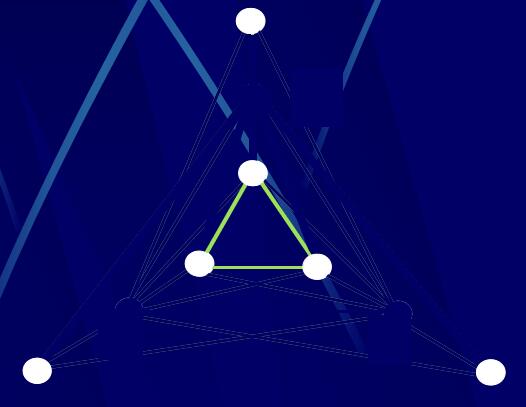
定理4.4.1： 如果图G=(P, L)是Hamilton图，则对P(G)的任一非空子集S，都有W(G－S) \(\leqslant\) |S|（连通分支数小于等于去掉的点的个数）

其中：
|S| 表示集合S的元素数，S就是删除的点集
G－S表示在G中删除S中的点以及以S中的点为端点的所有边而剩下的图（诱导子图），
W(G－S)表示图G－S的连通分支数。

常用其逆否命题用来证明该图不是Hamilton图（如果连通分支数大于去掉的点的个数则不是Hamilton图）

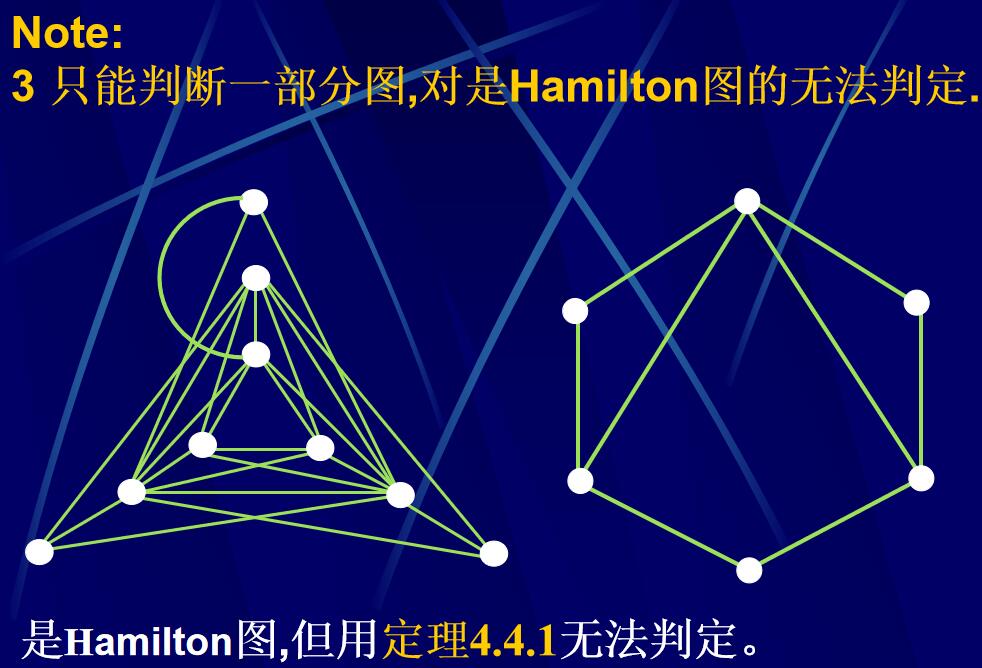
Hamilton图的充分条件

定理4.4.2：若G=(P, L)是有限图\(\gamma \geqslant 3\text{，}\delta \geqslant \gamma /2\)，则G是Hamilton图。

其中，\(\gamma\)表示图G中点数，即\(\gamma\)=|P(G)|，
\(\delta\)表示G中点的最小度。

白话：点数大于等于3，点的最小度大于等于点总数的二分之一

引理4.4.1：设G是有限图，u, v是G中不相邻的两点，并且满足：d(u)+d(v) $\geqslant \gamma $，则G是Hamilton图的充要条件是G∪{uv}是Hamilton图。

闭合图：设G是有限图。反复连接G中不相邻的并且其度之和不小于\(\gamma\)的点对，直到没有这样的点对为止。最后所得的图称为G的闭合图，记为C(G)。

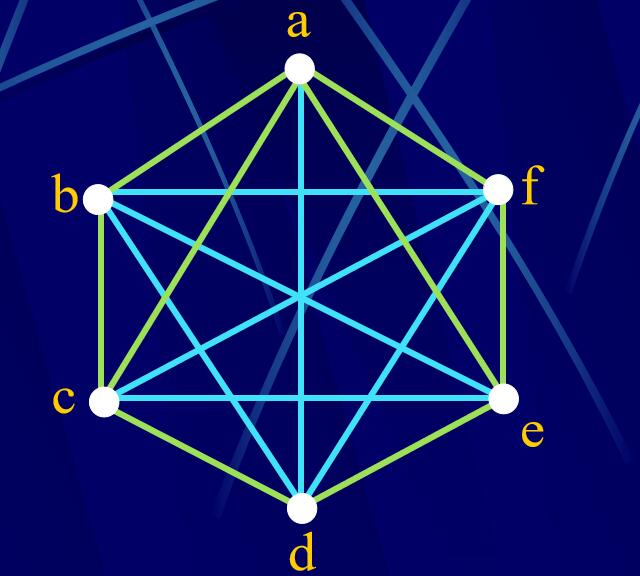
引理4.4.2 ：有限图G的闭合图C(G)是唯一确定的

定理4.4.3：有限图G是Hamilton图的充要条件是闭合图C(G)是Hamilton图。

推论：设G是有限图，若C(G)是完全图，则G是Hamilton图

推论的逆不成立：若G是Hamilton图,则C(G)未必是完全图

（定理4.4.3强于4.4.2）

常用结论：若一个图G的任意两点度数之和≥n-1，n=|P(G)|≥3，则该图有Hamilton路。

证明：

向图G中增加一个点v，并且连接v点与G中已有的n个点，设得到的图为G’， 这样：G’中点v的度为n，G中的n个点在G’中的度分别增加了1；从而有：G’中来自G的任意两个点的度数之和≥n-1+1+1=n+1；
而G’中v点与其他任意点的度数之和≥n+1；这样，G’中任意两点度数之和≥n+1=|P(G’)|。

则G’的闭合图是完全图，根据定理4.4.3的推论，可知G’是Hamilton图，则G’中有Hamilton回路，形如：

而且这条H回路只用了\(\mathrm{vv}_1\), \(\mathrm{vv}_n\)这两条新增加到G中的边，从而删除v点，G中存在Hamilton路.

定理4.4.4 ：设有限图G的度序列（即G的各点的度,按非降序排成的序列）为（d1,d2,…,\(d_{\gamma}\)），其中d1\(\leqslant\)d2\(\leqslant\)…\(\leqslant\)\(=d_{\gamma}\)，\(\gamma\) \(\leqslant\) 3.
如果不存在这样的m, m< \(\gamma\)/2 ，并使得\(d_m\)\(\leqslant\) m , \(d_{\gamma -m}\leqslant \gamma -m\)则G是Hamilton图。

定理4.4.4强于定理4.4.2

定义4.4.4 ：实数序列(p1, …, pn)称为由实数序列(q1, …, qn)所增大,如果pi\(\leqslant\)qi, i=1,…,n 称为不减度序列

例如: (2, 2, 2, 2)由(2, 2, 3, 3)所增大

定义4.4.5： 设G，H是有限图。G称为被H度增大，如果|P(G)|=|P(H)|，并且G的不减度序列被H的不减度序列所增大

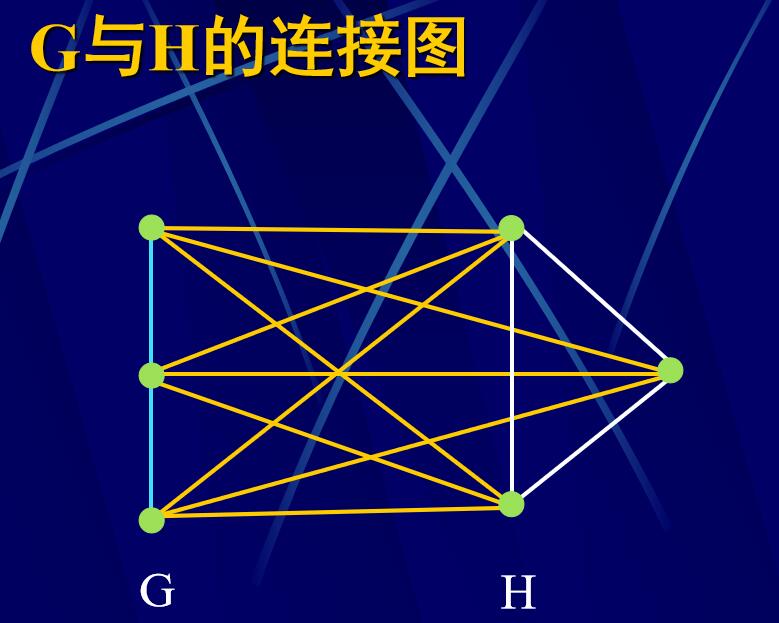
定义4.4.6 ：设G，H是两个无公共点的有限图。将G的每个点和H的每个点都用边连接起来得到的图，称为G与H的连接图

定义4.4.7： 设G，H是两个有限图，如果P(G)=P(H)，并且对G，H中任意两点u、v，u和v在G中相邻当且仅当它们在H中不相邻，则称G是H的补图，H是G的补图，可以将G记为\(\mathrm{H}_{\mathrm{c}}\)，也可将H记为\(\mathrm{G}_{\mathrm{c}}\)

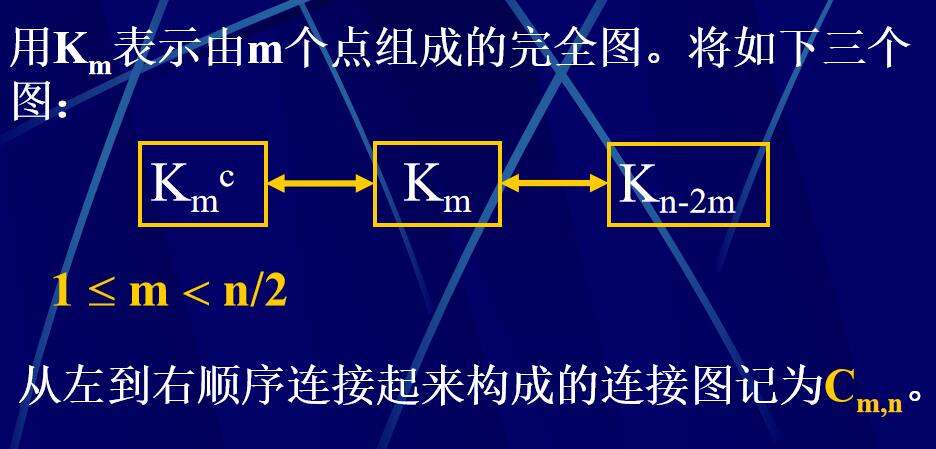
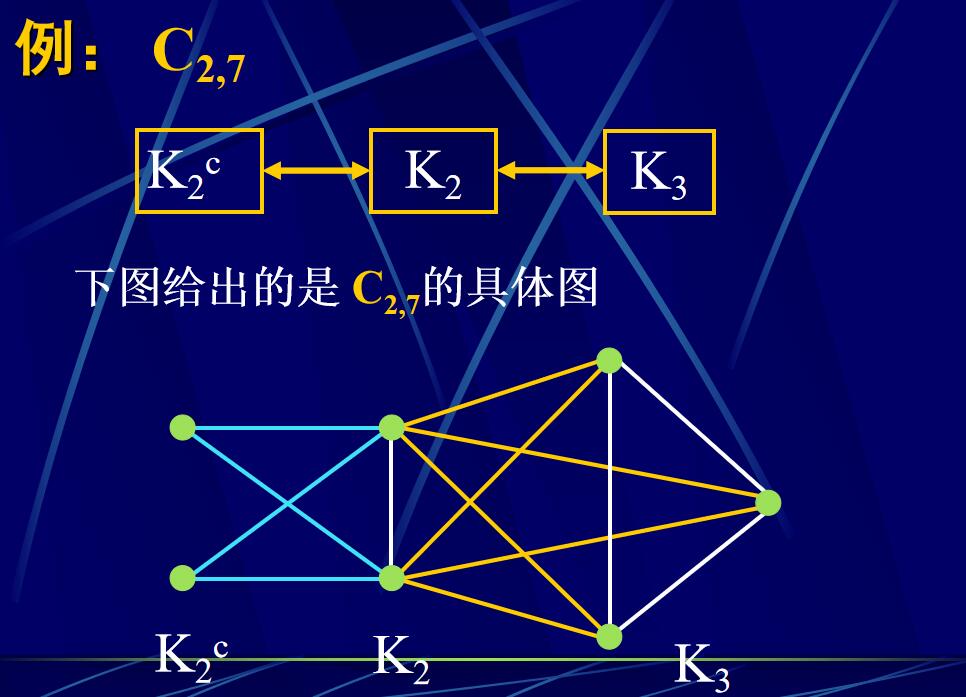
引理4.4.3：若1 \(\leqslant\) m < n/2 ，则图 \(\mathrm{C}_{\mathrm{m},\mathrm{n}}\)是非Hamilton图

定理4.4.5：若G为非Hamilton图，\(\mathrm{\gamma}\geqslant\) 3，则G由某个\(\mathrm{C}_{\mathrm{m},\mathrm{n}}\)所度增大。其中\(\gamma\)是P(G)的元数。该定理的逆定理不成立

连接图\(\mathrm{C}_{\mathrm{m},\mathrm{\gamma}}\)的不减度序列是

例如

例题:

常用结论：

设G是图，P(G)=n，L(G)=m，若 m≥\(\frac{1}{2}\)(n-1)(n-2)+2=\(\mathrm{C}_{\mathrm{n}-1}^{2}+2\)，则G一定是Hamilton图。

n个点的边数最多的非Hamilton图是边数为 \(\frac{1}{2}\)(n-1)(n-2)+1=\(\mathrm{C}_{\mathrm{n}-1}^{2}+1\)的图。(即n个点的边数最多的非Hamilton图是\(\mathrm{C}_{1,\mathrm{n}}\))

理解：之前讲过当边数m>\(\mathrm{C}_{\mathrm{n}-1}^{2}\)时也就是m\(\geqslant\)\(\mathrm{C}_{\mathrm{n}-1}^{2}\)+1时图必定连通，此时可以理解成1个点p和\(\mathrm{K}_{\mathrm{n}-1}\)这个完全图相连。此时没有哈密顿回路，不是哈密顿图，如果把这个点p和\(\mathrm{K}_{\mathrm{n}-1}\)中的任意一个点相连，由于\(\mathrm{K}_{\mathrm{n}-1}\)是哈密顿图，p到\(\mathrm{K}_{\mathrm{n}-1}\)有路，从\(\mathrm{K}_{\mathrm{n}-1}\)到p有另一条路，这就形成了哈密顿回路，也就是形成了哈密顿图

往期回顾

离散数学（集合论）
离散数学（古典数理逻辑）
离散数学（图与网络）
离散数学（数论基础）
离散数学（格与布尔代数）
离散数学（群、环、域）