离散数学(集合论)
集合的基本概念
集合的元素
属于\(\in\)
空集\(\varnothing\) 全集
有限集 、无限集
集合的元素数(基数):特别的:| \(\varnothing\) |=0,|{\(\varnothing\)}|=1
集合的特征:确定性、互异性、无序性、多样性
集合相等:两个集合A和B的元素完全一样
子集(subset) :设A,B是两个集合,若A的元素都是B的元素,则称A是B的子集,也称B包含A,或A包含于B记以A \(\subseteq\)B
若A\(\subseteq\)B,且A\(\ne\)B,则称A是B的真子集(proper subset),也称B真包含A,或A真包含于B,记以A\(\subset\)B
集合的运算及性质:
并集(Union):

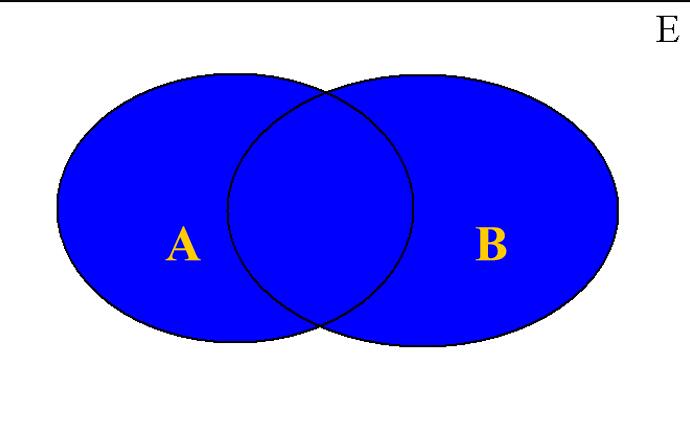
交集(Intersection):

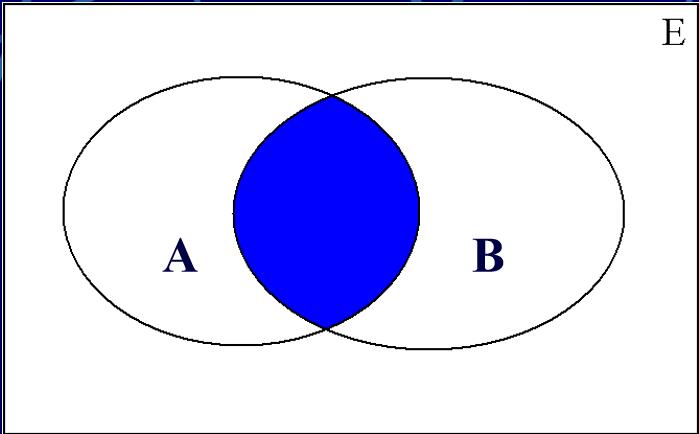
差集(Difference):


余集(Complement):


环和(对称差):


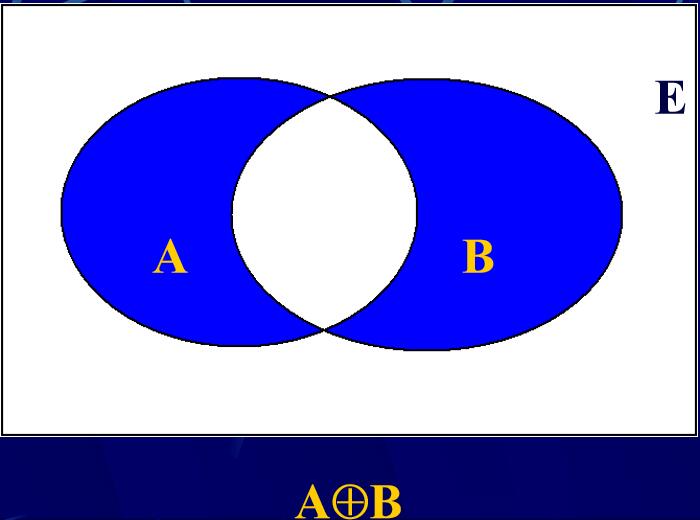
环积:


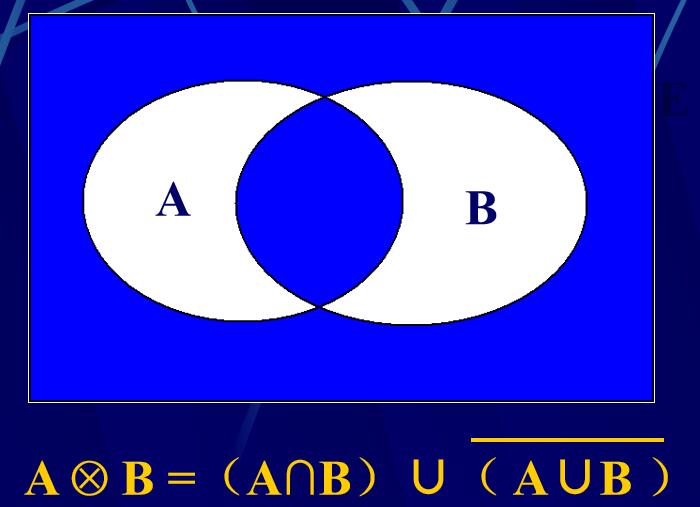
集合的算律:


集合的证明题:


集合的幂与笛卡尔积:
幂集的性质:
2.

3.

有序n元组(ordered n-tuple):(a1,a2 ,… ,an)
有序对(ordered pairs):当n=2 时,将其称作有序对,也称作序偶,或有序二元组
有序对特点:
- 若a\(\ne\)b,则(a,b)\(\ne\)(b,a)
- 两个有序对(a,b)和(c,d)相等当且仅当a=c,b=d
笛卡儿积(Cartesian product):

笛卡儿积的性质:
-
|A\(\times\)B|=|A| \(\times\)|B|;
-
对任意集合A,有A\(\times\)\(\varnothing\)=\(\varnothing\),\(\varnothing\)\(\times\)A=\(\varnothing\);
-
笛卡儿积运算不满足交换律,即A\(\times\)B\(\ne\)B\(\times\)A;
-
笛卡儿积运算不满足结合律,即(A\(\times\)B)\(\times\)C\(\ne\)A\(\times\)(B\(\times\)C)
-
笛卡儿积运算对并和交运算满足分配律
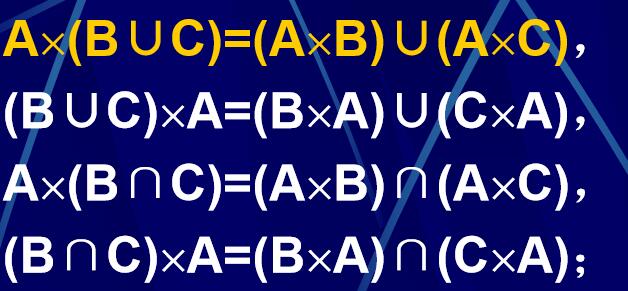
-
设A,B,C,D是集合,若A\(\subseteq\)C且B\(\subseteq\)D,则A\(\times\)B \(\subseteq\) C\(\times\)D。
证明集合的包含关系的常用方法:
- 利用定义:首先任取x\(\in\)A,再演绎地证出x\(\in\)B成立
- 设法找到一个集合T,满足A\(\subseteq\)T且T\(\subseteq\)B,由包含关系的传递性有A\(\subseteq\)B.
- 利用A\(\subseteq\)B的等价定义,即A\(\cup\)B=B,A\(\cap\)B=A或A-B=\(\varnothing\)来证.
- 利用已知包含式的并、交等运算得到新的包含式
- 反证法
证明集合相等的常用方法:
-
若A,B 是有限集,证明A=B可通过逐一比较两集合所有元素均一一对应相等,若A,B 是无限集,通过证明集合包含关系的方法证A \(\subseteq\) B,B \(\subseteq\) A即可
-
反证法
-
利用集合的基本算律以及已证明的集合等式,通过相等变换将待证明的等式左(右)边的集合化到右(左)边的集合,或者两边同时相等变换到同一集合

关系
非空集合中的空关系是反自反的、对称的、反对称的和传递的,但不是自反的;
空集合中的空关系则是自反的、反自反的、对称的、反对称的和传递的。
关系的定义:xRy
关系的特点:
-
A\(\times\)A的任一子集都是A上的一个关系
-
若|A|=n,则A上的关系有\(2^{\mathrm{n}^2}\)个
-
A上有三个特殊关系,即
空关系\(\varnothing\);
全域关系EA=A\(\times\)A;
相等关系IA={(x,x)|x\(\in\)A}
关系的表示:
-
集合表示:
设A={1,2,3,4}, A上的关系R=
-
关系矩阵
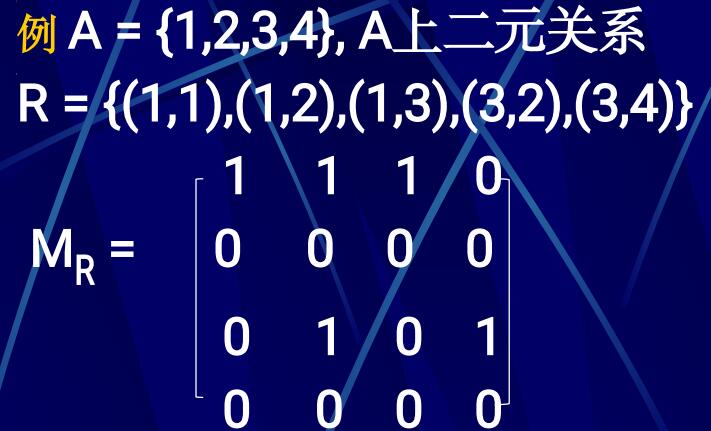
-
关系图:
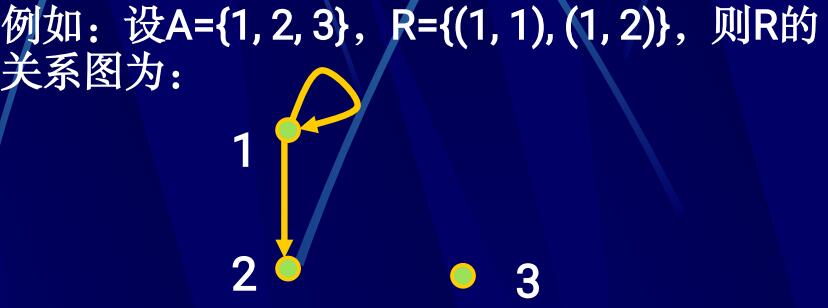
关系作为集合的运算:
- 关系的交:R ∩ S={(x,y)|x\(\in\)A, y\(\in\)A,xRy且xSy}
- 关系的并:R∪ S={(x,y)| x\(\in\)A, y\(\in\)A ,xRy或xSy}
- 关系的差:R - S={(x,y)| x\(\in\)A, y\(\in\)A ,xRy并且xS/y}
逆关系:\(\mathrm{R}^{-1}\) ={(y, x)|x\(\in\)A, y\(\in\)A, 并且有xRy}
关系的乘积:称关系R•S为关系R和S的乘积或合成
关系的乘法的结论:
- 关系的乘法不满足交换律
- 关系的乘法满足结合律

关系的幂

定理1.2.1 :
- \(\mathrm{R}^{\mathrm{m}}\cdot \mathrm{R}^{\mathrm{n}}=\mathrm{R}^{\mathrm{m}+\mathrm{n}}\)
- \(\left( \mathrm{R}^{\mathrm{m}} \right) ^{\mathrm{n}}=\mathrm{R}^{\mathrm{mn}}\)
定理1.2.3:

几种特殊关系及特点:
-
自反关系:

-
反自反关系


-
对称关系

-
反对称关系

-
传递关系

定理1.2.4 :集合A上的关系R具有传递性的充要条件是\(\mathrm{R}^2\subseteq \mathrm{R}\)
常用结论:
集合A上的关系是对称的,反对称的,试指明关系R的结构——\(\mathrm{I}_{\mathrm{A}}\)的任意子集
集合A有n个元素,则A上有多少个即具有对称性又具有反对称性的关系? \(2^{\mathrm{n}}\)(取对角线元素)
关系的性质总结:
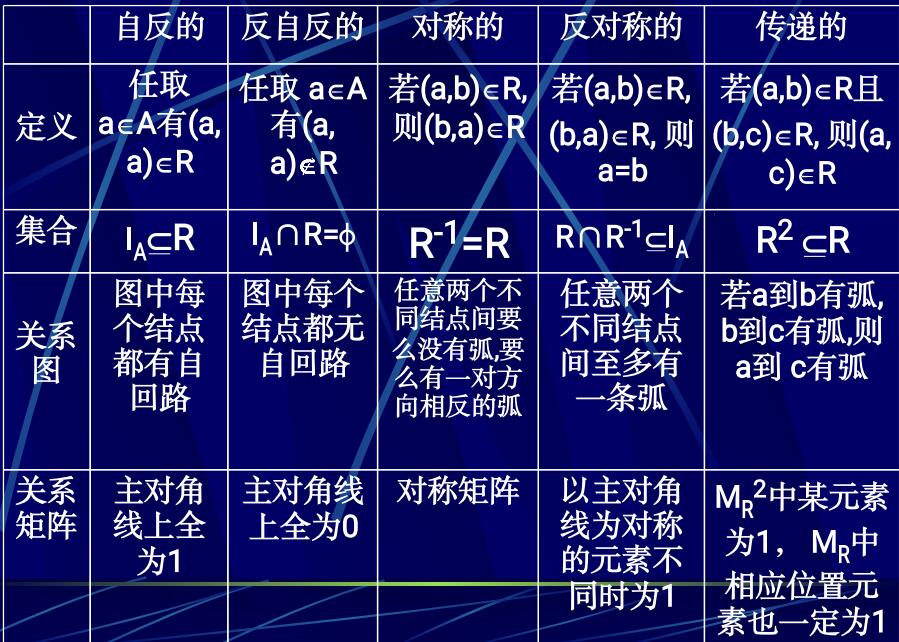
关系的闭包:R 的自反闭包、对称闭包和传递闭包分别记为r(R),s(R),t(R) ,也称r, s,t为闭包运算,它们作用于关系R后,产生包含R的最小的自反、对称、传递的关系。

等价关系:如果R具有自反性,对称性,传递性,则称R是一个等价关系
等价类

定理1.2.7:

划分:

商集:设R是非空集合A上的等价关系,以R的所有不同等价类为元素作成的集合称为A关于R的商集,简称A的商集,记作A/R


等价关系=>商集:

商集=>等价关系:

定理1.2.8 :设A为一个非空集合。
(1)设R为A上的任意一个等价关系,则对应R的商集A/R为A的一个划分。
(2)设C为A的任一个划分,令\(\mathrm{R}_{\mathrm{c}}\)={(x,y)|x, y\(\in\)A并且x, y属于C的同一划分块}, 则\(\mathrm{R}_{\mathrm{c}}\)为A上的等价关系
第二类Stirling数 :
将n个不同的球放入r个相同的盒中去,并且要求无空盒,有多少种不同的放法?这里要求n\(\geqslant\)r。
不同的放球方法数即为将n元集合A分为r块的不同的划分数。
(1)特值:
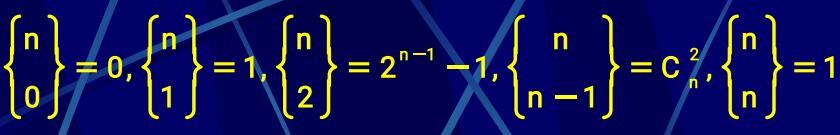
(2)递推公式:
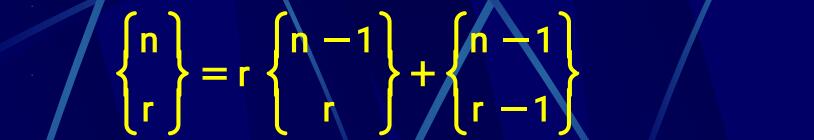

加细:设C和C'都是集合A的划分,若C的每个划分块都包含于C'的某个划分块中,则称C是 C '的加细。

C是C'的加细当且仅当\(\mathrm{R}_{\mathrm{c}}\)$\subseteq $$\mathrm{R}_{\mathrm{c'}}$
综合例题:


偏序关系:
自反性,反对称性,传递性
偏序集(半序集、部分序集)。记作(A,R)
写做“≤”
哈斯图:


链:
对任意x, y\(\in\)A,如果x≤y,或y≤x,称x与y可比
一个部分序集的子集,其中任意两个元素都可比,称该子集为一条链
全序集:一个部分序集(A, ≤)说是一个全序集,如果(A, ≤)本身是一条链

拟序关系:
反自反性,反对称,传递性
最大(最小)元 极大(极小)元 :只从给定集合里找

上(下)界,上(下)确界:从全体里找
上(下)确界:找所有上(下)界里距离所求集合最近的上(下)界。

上下界未必存在,存在时又未必唯一.
即使有上下界时,最小上界和最大下界也未必存在。
映 射
映射:设A,B是两个集合,若对A的每个元素a,规定了B的一个确定元素b与之对应,则称此对应为由A到B内的一个映射
将此映射记为\(\mathrm{\sigma}\),于是对任意a\(\in\)A,若\(\mathrm{\sigma}\)(a)= b,则b表示B中与a对应之元素,b称为a的映像(image),a称为b的原像(pre-image)
满射:设\(\mathrm{\sigma}\)是A到B内的映射,如果B中每一个元素都一定是A中某元素的映像,就称\(\mathrm{\sigma}\)是A到B上的映射(满射)
白话:B中所有元素都被箭头指向。
特别,A到A上的映射,称为变换

单射:设\(\mathrm{\sigma}\)是A到B内的映射,如果对任意a\(\in\)A,b\(\in\)A且a\(\ne\)b,都有\(\mathrm{\sigma}\)(a) \(\ne\)\(\mathrm{\sigma}\)(b),就称\(\mathrm{\sigma}\)是A到B的单射
白话:B中的元素最多只能有一个箭头指向。
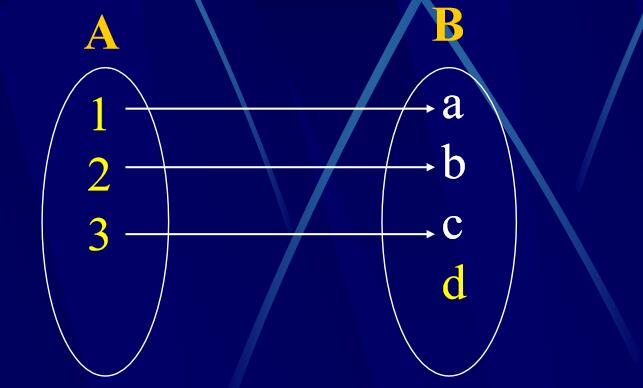
注意:单射未必满射;满射未必单射
1-1映射(双射):既满射,又单射。
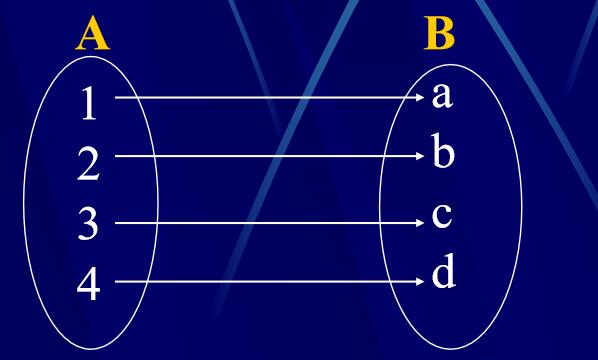
逆映射
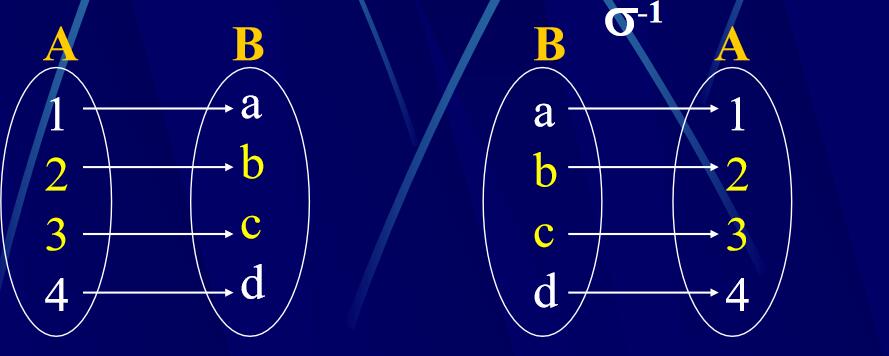
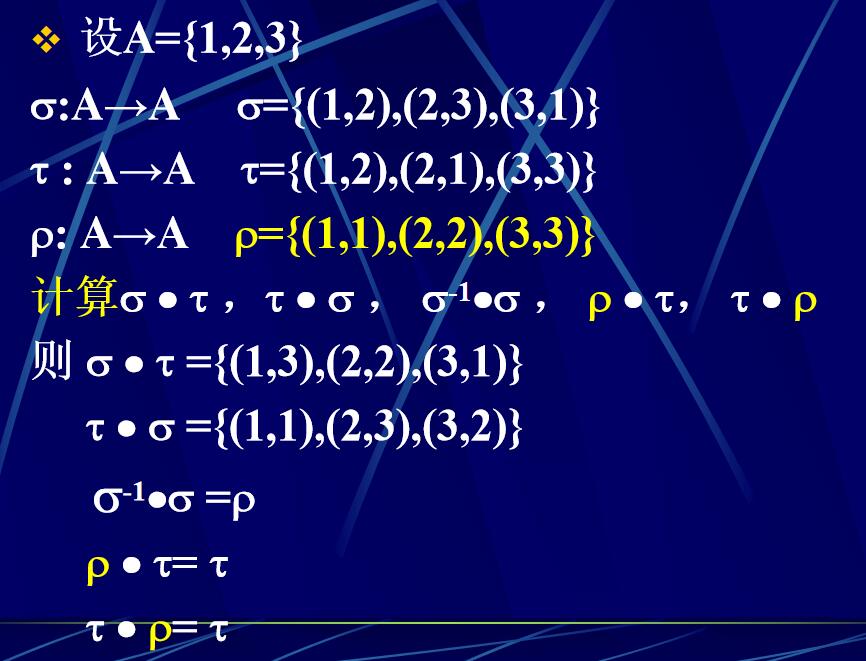
映射的乘积:\(\mathrm{\sigma}\cdot \mathrm{\tau}=\mathrm{\tau}*\mathrm{\sigma}\)(运算顺序相反)
集合的基数 :有限集合的元素数(势,浓度)。集合A的基数记为|A|
1-1映射,则称A与B基数相同,也称A与B对等(等势,等浓),记为|A|=|B|
把自然数集合的基数记为\(\aleph _0\)(读作阿列夫零),于是凡是与自然数集合对等的集合A,其基数|A|=\(\aleph _0\)
若A与B的某一子集有1-1对应关系,则|A|\(\leqslant\)|B|;若A与B的某一子集有1-1对应关系,且A与B不存在1-1对应关系,则|A|<|B|
可数集合:
一个集合,如果它的元素为有限个,或者它与自然数集合之间存在一个1-1映射,则称此集合为可数集合。否则称该集合为不可数集合。元素个数不是有限的可数集合称为可数无穷集合。
定理1.3.2:可数集合的子集仍为可数集合。
定理1.3.3: 设A,B是可数集合,A∩B= \(\varnothing\) ,则A∪B是可数集合
定理1.3.4:设A,B是可数无穷集合,则A\(\times\)B是可数集合。
常用结论:
有理数集合Q是可数集合
整数的集合Z是可数无穷集
可数无穷多个可数集合的并集是可数集合。
不可数集合:
定理1.3.5 :全体实数做成的集合是不可数集合
推论:实数集合R,区间(a,+\(\infty\))、[a,b]、[a,b)、(a,b],其中a≠b,都是不可数的,且与区间(0,1)等浓。
把(0,1)区间内的实数集合的基数记为c,也记为\(\aleph _1\)。即c= \(\aleph _1\)
可数(无穷多)个基数为c的集合的并集基数仍为c
往期回顾
离散数学(集合论)
离散数学(古典数理逻辑)
离散数学(图与网络)
离散数学(数论基础)
离散数学(格与布尔代数)
离散数学(群、环、域)

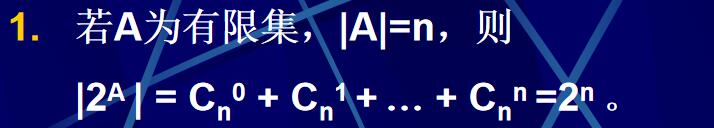

 浙公网安备 33010602011771号
浙公网安备 33010602011771号