八皇后（回溯法）

声明：图片及内容基于https://www.bilibili.com/video/av76265320

题目描述

在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法！

设计思路

皇后位置

用一维数组表示，数组下标是行，元素是列

int place[8] = { 0 };

冲突判断

flag保存哪一列已经存在皇后

bool flag[8] = { 1, 1, 1, 1, 1, 1, 1, 1 };

d1记录皇后的主对角线冲突

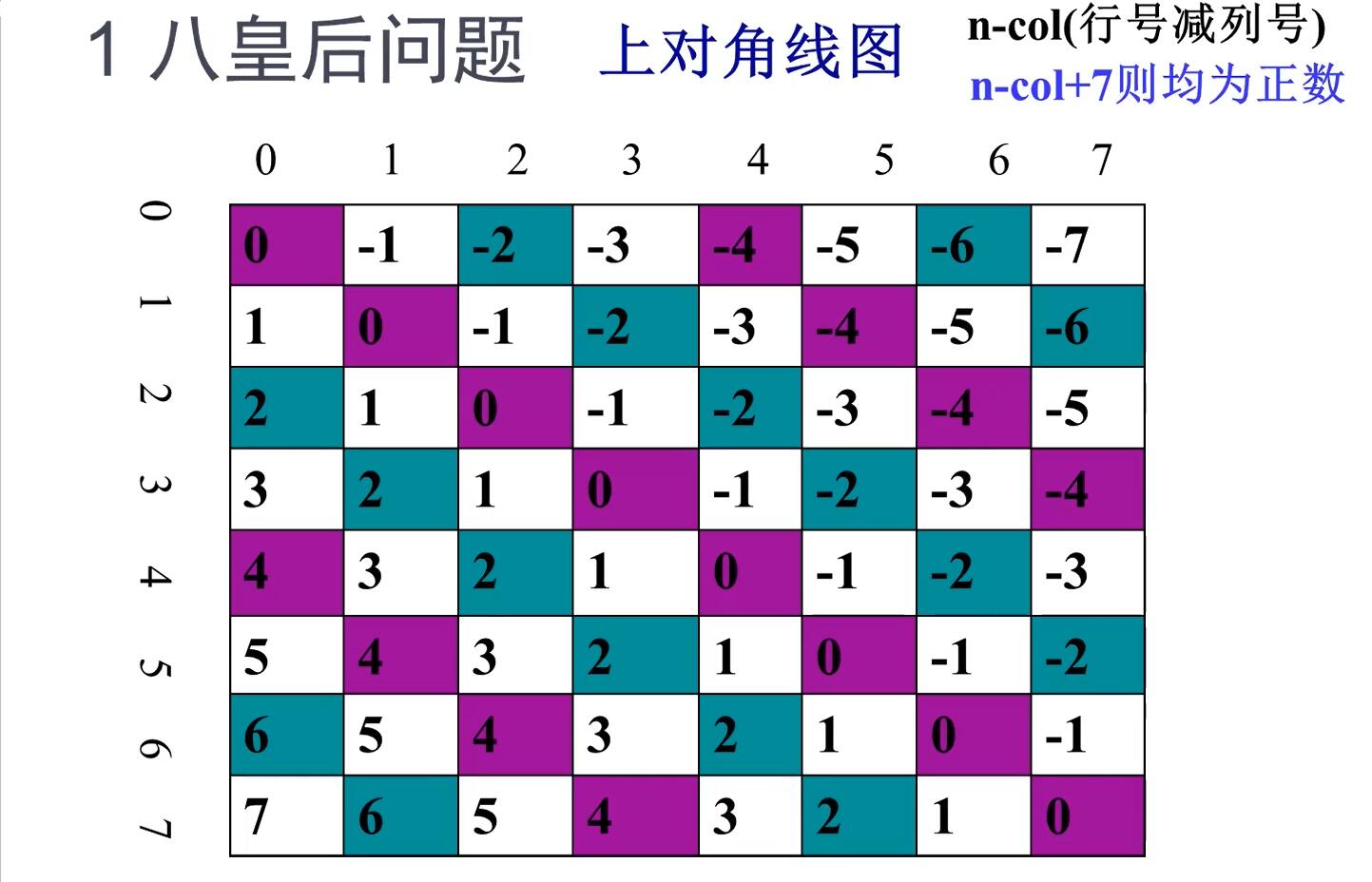
n - col + 7的范围是0~14对应d1[15]

bool d1[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };

 

d2记录皇后的次对角线冲突

d2 = n + col的范围是0~14对应d2[15]

bool d2[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1  };

八皇后核心

void QueenVIII(int n)         //n是行数
{
    for (int i = 0; i < 8; ++i)    // 每个皇后有8中可能的列 
    {
        if ((flag[i] && d1[n - i + 7]) && d2[n + i])    // 判断第n行第i列的位置是否危险
        {
            place[n] = i;        // 在第n行第i列摆放皇后 
            flag[i] = 0;        // 记录第i列已经有皇后了 
            d1[n - i + 7] = 0;    // 记录这条主对角线是危险的 
            d2[n + i] = 0;        // 记录这条次对角线是危险的

            if (n < 7 )            // 判断八个皇后放完了没有 
            {
                QueenVIII(n + 1);  //没放够就继续递归放 
            }
            else
            {
                output();        //放够八个皇后就输出
            }
            // 回溯（退回去看看有没有新方法） 
                flag[i] = 1;
                d1[n - i + 7] = 1;
                d2[n + i] = 1;
        }
    }
}

完整代码

# include <stdio.h>

// 全局变量
int place[8] = { 0 };    // 保存皇后的位置，下标为行，储存的数据为列。
bool flag[8] = { 1, 1, 1, 1, 1, 1, 1, 1 };    // 用来保存哪一列已经存在皇后 
bool d1[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 };    // 从左上到右下的对角线为上对角线，每条上对角线上的行和列的差是一样的。
bool d2[15] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1  };    // 从左下到右下的对角线为下对角线，每条下对角线上的行和列的和是一样的。
int key = 0;                    // 统计解的数量

// 函数声明
void QueenVIII(int);            // 八皇后问题
void output(void);                // 输出

// 主函数
int main(void)
{
    //output();
    QueenVIII(0);

    return 0;
}
void QueenVIII(int n)
{
    for (int i = 0; i < 8; ++i)    // 每个皇后有8中可能的列 
    {
        if ((flag[i] && d1[n - i + 7]) && d2[n + i])    // 判断第n行第i列的位置是否危险
        {
            place[n] = i;        // 在第n行第i列摆放皇后 
            flag[i] = 0;        // 记录第i列已经有皇后了 
            d1[n - i + 7] = 0;    // 记录这条上对角线是危险的 
            d2[n + i] = 0;        // 记录这条下对角线是危险的

            if (n < 7 )            // 判断八个皇后放完了没有 
            {
                QueenVIII(n + 1); //没放够就继续递归放 
            }
            else
            {
                output();        //放够八个皇后就输出
            }
            // 回溯（退回去看看有没有新方法） 
                flag[i] = 1;
                d1[n - i + 7] = 1;
                d2[n + i] = 1;
        }
    }
}

void output(void)
{
    printf("第%d种解法：\n", ++key);
    for (int n = 0; n < 8; ++n)
    {
        for (int i = 0; i < 8; ++i)
        {
            if (place[n] == i)  //有皇后的位置为 1
            {
                printf("1 ");
            }
            else
            {
                printf("0 ");
            }
        }
        printf("\n");
    }
    printf("\n");
}