树链剖分(强势借鉴)
树链剖分
概念
树链剖分 就是对一棵树分成几条链,把树形变为线性,减少处理难度
需要处理的问题:
- 将树从x到y结点最短路径上所有节点的值都加上z
- 求树从x到y结点最短路径上所有节点的值之和
- 将以x为根节点的子树内所有节点值都加上z
- 求以x为根节点的子树内所有节点值之和
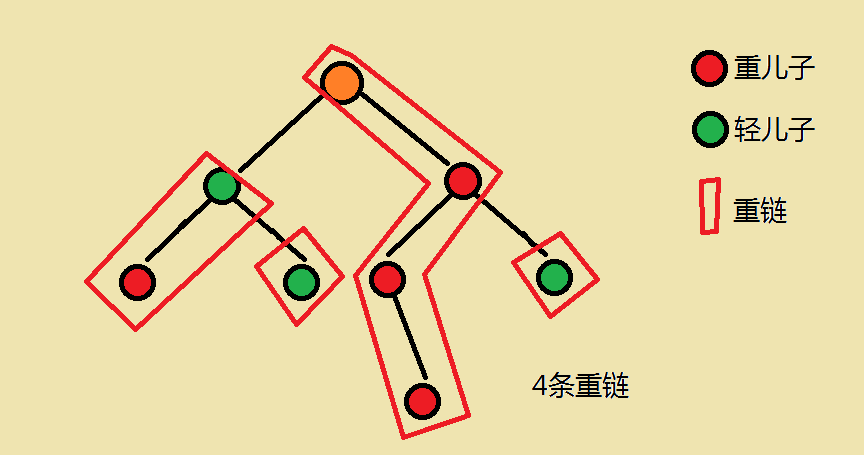
重儿子:对于每一个非叶子节点,它的儿子中 儿子数量最多的那一个儿子 为该节点的重儿子
轻儿子:对于每一个非叶子节点,它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
叶子节点没有重儿子也没有轻儿子(因为它没有儿子。。)
重边:连接任意两个重儿子的边叫做重边
轻边:剩下的即为轻边
重链:相邻重边连起来的 连接一条重儿子 的链叫重链
对于叶子节点,若其为轻儿子,则有一条以自己为起点的长度为1的链
每一条重链以轻儿子为起点
dfs1()
这个dfs要处理几件事情:
- 标记每个点的深度dep[]
- 标记每个点的父亲fa[]
- 标记每个非叶子节点的子树大小(含它自己)
- 标记每个非叶子节点的重儿子编号son[]
dfs2()
这个dfs2也要预处理几件事情
- 标记每个点的新编号
- 赋值每个点的初始值到新编号上
- 处理每个点所在链的顶端
- 处理每条链
顺序:先处理重儿子再处理轻儿子,理由后面说
处理问题
Attention 重要的来了!!!
前面说到dfs2的顺序是先处理重儿子再处理轻儿子
我们来模拟一下:
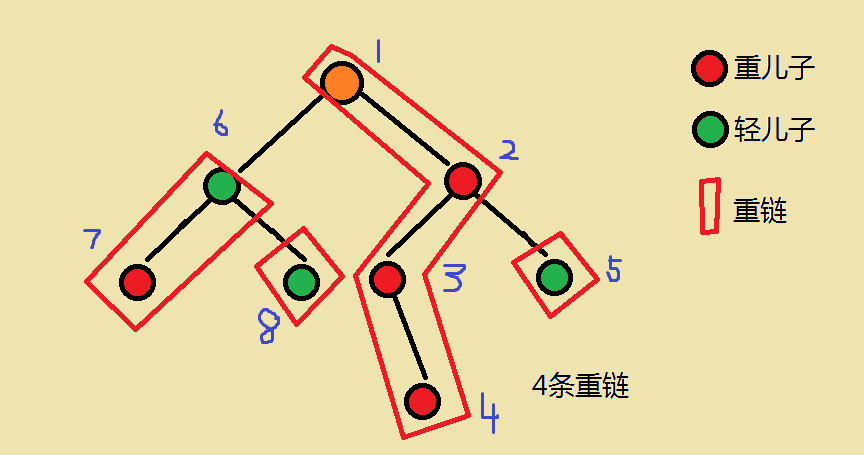
- 因为顺序是先重再轻,所以每一条重链的新编号是连续的
- 因为是dfs,所以每一个子树的新编号也是连续的
现在回顾一下我们要处理的问题
- 处理任意两点间路径上的点权和
- 处理一点及其子树的点权和
- 修改任意两点间路径上的点权
- 修改一点及其子树的点权
1、当我们要处理任意两点间路径时:
设所在链顶端的深度更深的那个点为x点
- ans加上x点到x所在链顶端 这一段区间的点权和
- 把x跳到x所在链顶端的那个点的上面一个点
不停执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
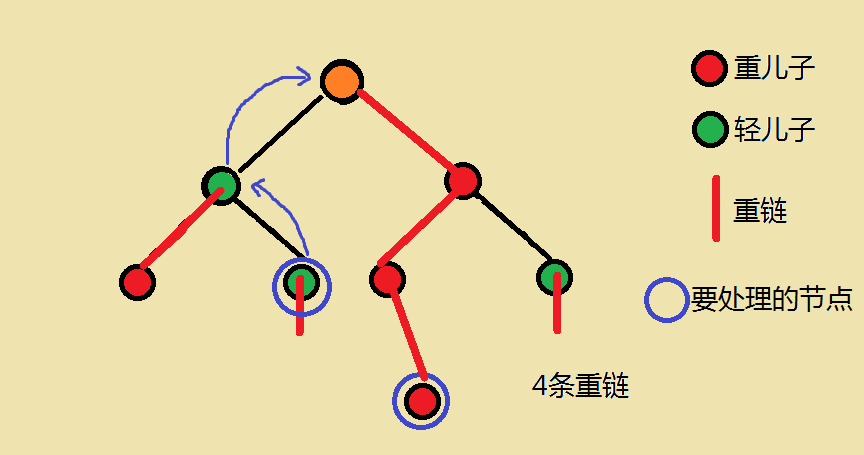
这时我们注意到,我们所要处理的所有区间均为连续编号(新编号),于是想到线段树,用线段树处理连续编号区间和
每次查询时间复杂度为O(log^2n)
例题
T1 模板 P3384 【模板】树链剖分
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
输入样例#1:
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出样例#1:
2
21
说明
时空限制:1s,128M
模板题
#include<bits/stdc++.h>
using namespace std;
inline int read()
{
int a=0,b=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-')
b=-1;
c=getchar();
}
while(isdigit(c))
{
a=(a<<1)+(a<<3)+(c^48);
c=getchar();
}
return a*b;
}
const int maxm=100005;
int n,m,r,p;
int a[maxm],sum[maxm<<2],lazy[maxm<<2];
struct node
{
int to,nxt;
}edge[maxm<<1];
int head[maxm],edge_num;
inline void added(int from,int to)
{
++edge_num;
edge[edge_num].to=to;
edge[edge_num].nxt=head[from];
head[from]=edge_num;
}
int fa[maxm],son[maxm],size[maxm],dep[maxm];
int dfn[maxm],num[maxm],top[maxm],cnt;
inline void build(int k,int l,int r)
{
if(l==r)
{
sum[k]=a[l]%p;
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
sum[k]=(sum[k<<1]%p+sum[k<<1|1]%p)%p;
}
inline void add(int k,int l,int r,int v)
{
sum[k]=sum[k]+(r-l+1)*v%p;
lazy[k]=(lazy[k]%p+v%p)%p;
}
inline void pushdown(int k,int l,int r)
{
if(!lazy[k])
return;
int mid=(l+r)>>1;
add(k<<1,l,mid,lazy[k]);
add(k<<1|1,mid+1,r,lazy[k]);
lazy[k]=0;
}
inline void insert(int k,int l,int r,int x,int y,int v)
{
if(x<=l&&r<=y)
{
add(k,l,r,v);
return;
}
int mid=l+r>>1;
pushdown(k,l,r);
if(x<=mid)
insert(k<<1,l,mid,x,y,v);
if(mid<y)
insert(k<<1|1,mid+1,r,x,y,v);
sum[k]=(sum[k<<1]%p+sum[k<<1|1]%p)%p;
}
inline int query(int k,int l,int r,int x,int y)
{
if(x<=l&&r<=y)
return sum[k];
pushdown(k,l,r);
int mid=l+r>>1;
int ret=0;
if(x<=mid)
ret=(ret+query(k<<1,l,mid,x,y))%p;
if(mid<y)
ret=(ret+query(k<<1|1,mid+1,r,x,y))%p;
return ret;
}
inline void dfs1(int u,int f,int depth)
{
dep[u]=depth;
fa[u]=f;
size[u]=1;
int maxn=-1;
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(v==f)
continue;
dfs1(v,u,depth+1);
size[u]+=size[v];
if(size[v]>maxn)
{
son[u]=v;
maxn=size[v];
}
}
}
inline void dfs2(int u,int root)
{
dfn[u]=++cnt;
a[cnt]=num[u];
top[u]=root;
if(!son[u])
return;
dfs2(son[u],root);
for(int i=head[u];i;i=edge[i].nxt)
{
int v=edge[i].to;
if(son[u]!=v&&fa[u]!=v)
dfs2(v,v);
}
}
inline void insert1(int x,int y,int v)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
insert(1,1,n,dfn[top[x]],dfn[x],v);
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
insert(1,1,n,dfn[x],dfn[y],v);
}
inline void insert2(int x,int v)
{
insert(1,1,n,dfn[x],dfn[x]+size[x]-1,v);
}
inline int query1(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
swap(x,y);
ans+=query(1,1,n,dfn[top[x]],dfn[x]);
ans%=p;
x=fa[top[x]];
}
if(dep[x]>dep[y])
swap(x,y);
ans+=query(1,1,n,dfn[x],dfn[y]);
return ans%p;
}
inline int query2(int x)
{
return query(1,1,n,dfn[x],dfn[x]+size[x]-1);
}
int main()
{
n=read();
m=read();
r=read();
p=read();
for(int i=1;i<=n;i++)
num[i]=read();
for(int i=1;i<n;i++)
{
int from,to;
from=read();
to=read();
added(from,to);
added(to,from);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--)
{
int opt,x,y,z;
opt=read();
if(opt==1)
{
x=read();
y=read();
z=read();
insert1(x,y,z);
}
else if(opt==2)
{
x=read();
y=read();
printf("%d\n",query1(x,y));
}
else if(opt==3)
{
x=read();
y=read();
insert2(x,y);
}
else if(opt==4)
{
x=read();
printf("%d\n",query2(x));
}
}
return 0;
}

