清北学堂2019.7.15
Day 3 丁明朔
首先,这个老师真是太666了,肯定给10分啊qwq
上午主要讲的就是一些基础
 (noip的基础内容)
(noip的基础内容)
1.堆
(1) 是priority_queue支持插入一个值
(2) 删除一个值
(3) 查询最大值或最小值
2.LCA(最近公共祖先)
(1) 应用:用来做树上最短路径
(2) 步骤
① 朴素算法:
1) 将深的结点放到a
2) 将a和b提到一个深度
a.这里可以进行二进制分解
3) 将两个点一起上移,知道二者相同为止
② 将3)优化
1) 其中,i表示该节点的第2^i个祖先:用p[x][i]=p[p[x][i-1]][i-1]记录
2) 用一个for(i由16到1)
a.直到p[a][i]!=p[p[x][i-1]][i-1]时,将两个点一起上移2^i个祖先
③ 处理差分时可以应用LCA
3.ST表
(1) 
(2) 将区间分为两个部分,计算l为区间长度则log l为2^j的值,即为mx数组的第二位意义
4.Hash
(1) 将字符串变成一个数
(2) map是一个基于比较函数的红黑树(很慢)
(3) 可能会有冲突(这时候可以取模【为大幅度避免冲突可以双模数】)方便的话可以直接unsigned long long
(4) 见笔记吧qwq
可以利用前缀hash,然后应用类似差分的方法搞
求hash(i,j)=hj-hi-1*pj-i+1
现将这个玩意初始化,注意要通过双取模的方式来减少数的取模后数相同的概率
5.并查集
(1) 标记集合
(2) 树根的父亲是他自己
(3) 路径压缩: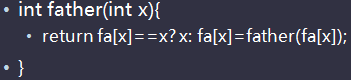 (大萌神的代码)
(大萌神的代码)
6.树状数组(大萌神说代码就一行qwq)
(1) 
(2) 树状数组存在的所有问题必须存在逆元
7.线段树
(1) 树的每一个结点是一个抽象的线段(二叉树)
(2) 各种玄学操作(代码)
这里主要是一些伪代码
struct Node{ int l,r; int sum; int tag; }t[N<<2]; void pushup(int rt){ t[rt].sum=t[rt<<1].sum+t[rt<<1|1].sum; } void pushdown(int rt){ if(t[rt].tag){ t[rt<<1].tag+=t[rt].tag; t[rt<<1].sum+=t[rt].tag*(t[rt<<1].r-t[rt<<1].l+1); t[rt<<1|1].tag+=t[rt].tag; t[rt<<1|1].sum+=t[rt].tag*(t[rt<<1|1].r-t[rt<<1|1].l+1); t[rt].tag=0; } } void build(int rt,int l,int r){ t[rt].l=l; t[rt].r=r; if(l==r){ t[rt].sum=a[l]; return; } int mid=(l+r)>>1; build(rt<<1,l,mid); build(rt<<1|1,mid+1,r); pushup(rt); } void modify(int rt,int p,int c){ if(t[rt].l==t[rt].r){ t[rt].sum=c; return; } pushdown(rt); int mid=(t[rt].l+t[rt].r)>>1; if(p<=mid) modify(rt<<1,p,c); else modify(rt<<1|1,p,c); pushup(rt); } int query(int rt,int l,int r){ if(l<=t[rt].l&&t[rt].r<=r){ return t[rt].sum; } pushdown(rt); int ret=0; int mid=(t[rt].l+t[rt].r)>>1; if(l<=mid) ret+=query(rt<<1,l,r); if(mid<r) ret+=query(rt<<1|1,l,r); return ret; } void add(int rt,int l,int r,int c){ if(l<=t[rt].l&&t[rt].r<=r){ t[rt].tag+=c; t[rt].sum+=c*(t[rt].r-t[rt].l+1); return; } pushdown(rt); int mid=(t[rt].l+t[rt].r)>>1; if(l<=mid) add(rt<<1,l,r,c); if(mid<r) add(rt<<1|1,l,r,c); pushup(rt); }
总结:

例题:


洛谷P1168 中位数
维护两个堆,一个大根堆大小为n/2+1,小根堆大小为n/2
然后大的放到小根堆,小的放到大根堆,这样可以保证大根堆堆顶为中位数
洛谷P1090 合并果子

#include<bits/stdc++.h> using namespace std; int n; priority_queue<int,vector<int>,greater<int> >h; void work() { int i,x,y,ans=0; cin>>n; for(int i=1;i<=n;i++) { cin>>x; h.push(x); } for(int i=1;i<n;i++) { x=h.top();h.pop(); y=h.top();h.pop(); ans+=x+y; h.push(x+y); } cout<<ans; } int main() { work(); }
用哈夫曼树好像比较简单(就是比较快)
然鹅我并不会qwq

这个貌似是用k叉哈夫曼树,但是老师没有讲

先按高度差排一个序,小的先加入图,合并两节点,运用并查集,并且统计树的大小,当有一个集合的大小大于等于t时,这个集合的难度评级就都知道了,为最后所加入的边的边权。


重心:以一点为根,其子树的最大节点数最小
括号序列:封闭括号为叶子节点,以此类推,则计算其hash值

1.归并排序
2.统计前面有多少个小于等于它的,再用总数去减
为了让他更加的简单,需要离散化
先排序再unique最后用lower_bound
(算是一种模型)

↓二维偏序 xi<=xj yi<=yj
按照y的升序处理星星,所以在处理时只需要我们去处理x的特点就可以了(树状数组)

10个树状数组 分别记录mod m为几的数个数
加减号做 询问时输出模数所在树状数组l~r个数即可



运用矩阵乘法就好了外加线段树

开根号:
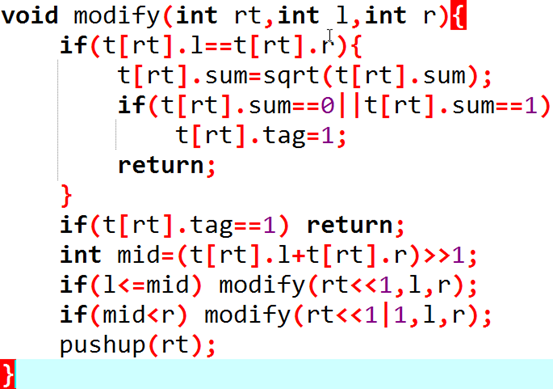


建一棵线段树,大小为l到r之内的数,在长度为5的数组中长什么样子,以及大小在l到r中出现了几次

Mex表示未出现过得最小非负整数


若以某一个数对称,则不会有等差数列
二叉查找树:
左子树小于该节点,右子树大于该节点
伸展树:通过伸展,让树的深度不这么深。
伸展操作基于元操作——》旋转(rotate)



