清北学堂培训2019.4.30
Day 3(钟皓曦)
期待中的钟神终于来了(果不其然带来了摸鱼时间qwq)
emmm,谈些正经的话题
今天算是一个有关于DP(动态规划)的全集
那么我来介绍一下有关DP的知识
DP(动态规划)
【具有无后效性(先不管是什么)】
以斐波那契数列为例 { 据钟神说通项公式为:fn=【(sqrt(5)+1))/2】n-【(sqrt(5)-1))/2】n }
 (←斐波那契数列就是这么个东西)
(←斐波那契数列就是这么个东西)
边界条件:f0=0,f1=1
转移方程:fn=fn-1+fn-2
方法:
- 顺着推
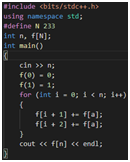
- 逆着推
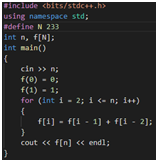
- 记忆化搜索
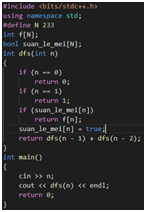
常见的DP:
- 数位DP
- 树形DP
- 状压DP
- 其他DP(可能性最大)
- 区间DP
- 插头DP(应该不会考)
- 博弈论DP(应该不会考)
数位DP:
按照数字的位数划分转移阶段
转移方式:枚举下一位数字填什么
限制条件:数位的上下界要求
例题:
给定两个数l,r;求l—r之间有多少个数?
思路:
将这个数按位拆开,【0-x】拆成xn位
原式化为【0-r】–【0-l-1】
则需求v,满足0≤v≤x,数位DP从最高位开始填
分以下两种情况:
- x前几位大于v前几位,则剩下的随便填
- x前几位等于v前几位,则x剩下的大于v剩下的
- f【i】【j】表示这种情况的方案数;i表示已经填好了i位;j=0表示x前i位大于v前i位;j=1表示x前i位等于v前i位
那么需要枚举第i-1位填什么,即可求解。
#include <bits/stdc++.h> using namespace std; int l, r, z[233]; int f[23333][2]; int solve(int x) { int n = 0; while (x) //求出x的每一位 { z[n] = x % 10; x /= 10; n++; } n--; memset(f, 0, sizeof(f)); f[n + 1][1] = 1; for (int i = n; i >= 0; i--) { for (int j = 0; j <= 1; j++) { //先分类讨论 if (j == 0) { for (int k = 0; k <= 9; k++) { f[i][0] += f[i + 1][j]; } } else { for (int k = 0; k <= z[i]; k++) { //继续分类讨论 if (k == z[i]) { f[i][1] += f[i + 1][j]; } else { f[i][0] += f[i + 1][j]; } } } } } return f[0][0] += f[0][1]; } int main() { cin >> l >> r; cout << solve(r) - solve(l - 1) << endl; return 0; }
例题;
l-r的数的数位的和?
例题:
求l-r中满足相邻两个数字之差至少为2的个数有多少个?
直接看代码吧qwq
#include <bits/stdc++.h> using namespace std; int l, r, z[233]; int f[23333][2], g[23333][2]; int solve(int x) { int n = 0; while (x) //求出x的每一位 { z[n] = x % 10; x /= 10; n++; } n--; memset(f, 0, sizeof(f)); memset(g, 0, sizeof(g)); f[n + 1][1] = 1; g[n + 1][1] = 0; for (int i = n; i >= 0; i--) { for (int j = 0; j <= 1; j++) { //先分类讨论 if (j == 0) { for (int k = 0; k <= 9; k++) { f[i][0] += f[i + 1][j]; g[i][0] += g[i + 1][j] + f[i + 1][j] * k; } } else { for (int k = 0; k <= z[i]; k++) { //继续分类讨论 if (k == z[i]) { f[i][1] += f[i + 1][j]; g[i][0] += g[i + 1][j] + f[i + 1][j] * k; } else { f[i][0] += f[i + 1][j]; g[i][0] += g[i + 1][j] + f[i + 1][j] * k; } } } } } return g[0][0] += g[0][1]; } int main() { cin >> l >> r; cout << solve(r) - solve(l - 1) << endl; return 0; }
好像是Windy数(不过我不知道有什么区别qwq)
思路:
题目中有多少条件,就用多少个维度去解决问题。
所以加一个维度k;
f【i】【j】【k】表示这种情况的方案数;i表示已经填好了i位;j=0表示x前i位大于v前i位;j=1表示x前i 位等于v前i位;k表示第i位填了k
这个直接去做吧(毕竟题解比我讲的好qwq)
树形DP:
按照树从根往下或者叶子往上划分阶段
删除方式:集合叶子或者父亲的信息
限制条件:不详(不是我骗你们,是真的不详qwq)
若f【i】表示以i为根的子树有多少个点
则易得f【leaf】=1
可以推得:f【p】=f【son 1】+ f【son 2】+······=+f【son k】+1(设p有k个儿子)
//计算根为i的子树的结点个数(伪代码) #include <bits/stdc++.h> using namespace std; int n, f[233]; void dfs(int p) { for (x) //x表示p的各个儿子 { dfs(x); f[p] += f[x]; } f[p]++; } int main() { cin >> n; read_tree(); //读入树先暂时不写 dfs(1); //以一为根树的大小 cout << f[1] << end; return 0; }
例子:
求任一个树的直径(最远两个点的距离)
我们可以清楚的看到:
这个最远的距离一定是这样的:↗↘(使得路径尽量的长)
即求下一个点向下走的最长和次长路径的和。
状态定义:
f【i】【0】表示i向下最长;f【i】【1】表示i向下次长。
转移方程:
所以说f【p】【0】=max(f【p 1】【0】+ f【p 2】【0】+······+f【p k】【0】)+1(设p有k个不同的到达叶子路径)
f【p】【1】=max(f【p 1】【0】+ f【p 2】【0】+······+f【p k】【0】)+1(设p有k个不同的到达叶子路径)【在 f【p 1】【0】+ f【p 2】【0】+······+f【p k】【0】中把之前求的最大值去掉】
最后答案还应该将 f【p】【0】+f【p】【1】-1
练习题:
洛谷 P4408 [NOI2003]逃学的小孩 洛谷 P3304 [SDOI2013]直径
区间DP(据说相对简单)
思想:一定是枚举一个断点从而进行合并
例子:
【洛谷【NOI1995】石子合并】的非环状况
n堆石头,每次可以合并相邻两堆石子,合并两堆石头代价为两堆石头之和,求合并为一堆石头时所花的代价最小。
不难发现,一定可以找到一条分界线p,使得左边【l-p】和右边【p+1-r】各合并成一堆石子
状态定义:
f【l】【r】表示从第l堆石子到第r堆石子合并为一堆石子的最小代价
边界条件:f【i】【i】=0
转移方程:
f【l】【r】=min(f【l】【r】,f【l】【p】+f【p+1】【r】+sum【l】【r】)
但在枚举的过程中需要满足一个阶段性:
for(int l=1;l<=n;l++) { for(int r=l+1;r<=n;r++) { for(int p=1;p<r;p++) { f[l][r]=min(f[l][r],f[l][p]+f[p+1][r]+sum[l][r]); } } }
这个代码显然不行,这显然不行,因为在算f【l】【r】时,f【p+1】【r】并没求出。
正解:
//石子合并(不是环的情况) #include <bits/stdc++.h> using namespace std; const int INF = 0x3f3f3f3f; //两个0x7f加起来爆int,推荐用0x3f int n, int main() { cin >> n; for (int i = 1; i <= n; i++) { cin >> z[a]; } memset(f, 0x3f, sizeof(f)); for (int i = 1; i <= n; i++) { f[i][i] = 0; } for (int len = 2; len <= n; len++) { for (int l = 1, r = len; r <= n; l++, r++) { for (int p = 1; p < r; p++) { f[l][r] = min(f[l][r], f[l][p] + f[p + 1][r] + sum[l][r]); } } } cout << f[1][n] << endl; return 0; }
就是复杂度有点高qwq,为O(n^3)
若为环,则需开两个n的空间,取min(f【1】【n】,f【2】【n+1】,f【3】【n+2】······)就可以了
因为这枚举了所有断点的情况
复杂度不变——O(n^3),序列长度变成两倍
练习题:
洛谷 P1880 [NOI1995]石子合并 洛谷 P1063 能量项链
状压DP:
按照选取集合的状态划分转移阶段
转移方式:枚举下一个要选取的物品
限制条件:不详(qwq)
先总结一下根据数据可以推出来的方法:
N<=22多半用状压
N<=12多半用爆搜
N<=32 多半放弃吧
N<=50多半放弃吧
N<=100多半O(n^3)
N<=1000多半O(n^2)
N<=10000 多半数据结构题O(nlogn)
N<=100000 多半线性的
N>100000 多半O(1)
这个方法是用做TSP问题(旅行商问题)
【属于NP—hard问题(复杂度至少为2^n)】
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
考虑状态压缩:
先设一个集合
若该点在这个集合里,则用二进制数1表示;反之为0
将这个二进制的数返回为一个十进制的数。
f【s】【i】:s表示这是一个s位的二进制数,i表示停留在i,数组表示这种情况最短距离
初始化:
f【1】【1】=0.
这里的转移方程大概是这么写的。(具体思路)
#include<iostream> #include<cstdio> #include<vector> #include<algorithm> #include<queue> #include<cstring> using namespace std; int read() { int f=1,x=0; char ss=getchar(); while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();} while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();} return f*x; } int n; int dp[1100010][25]; int map[25][25]; int main() { n=read(); for(int i = 1;i <= n;i ++) for(int j = 1;j <= n;j ++) map[i][j]=read();//读入个村庄间距离 memset(dp,63,sizeof(dp)); dp[1][1] = 0;//状态1表示此时只有1号点访问过 for(int i =0;i<=(1 << n) -1;i++) for(int j=1;j<=n;j++) if( !( (1 << j-1) & i) ) for(int k=1;k<=n;k++) if( ( (1 << k-1) & i) ) dp[((1 << j-1) | i)][j] = min(dp[((1 << j-1) | i)][j],dp[i][k] + map[k][j]);//核心代码,解释如上所述 int ans = 2147483640; for(int i=2;i<=n;i++)//最后从状态(1<<n)-1(二进制全为1)中寻找到1最短的点 ans=min(ans,dp[(1<<n)-1][i] + map[i][1]); cout<<ans; return 0; }
If(j∉这个集合s),则f【s∪{j}】【i】=f【s】【i】+dis【i】【j】
复杂度(n^2 * 2^n),内存O(2^n *n)
其他DP
洛谷1216
改编:使得最后%m后值最大
当一个题做不了的时候就往上加维度
考虑数据范围
状态定义:
bool f【i】【j】【k】表示走到第i行第j列%m=k是不是可能的
可能为true;不可能为false
所以,f【i】【j】【k】= f【i-1】【j-1】【k-aij】| f【i-1】【j】【k-aij】
边界条件:f【1】【1】【a11】=true
//数字三角形 #include <iostream> #include <cstdio> #include <cmath> using namespace std; int f[1001][1001], a[1001][1001], n; int main() { cin >> n; for (int i = 1; i <= n; i++) { for (int j = 1; j <= i; j++) cin >> a[i][j]; } f[1][1] = a[1][1]; for (int i = 2; i <= n; i++) { for (int j = 1; j <= i; j++) f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j]; } int ans = 0; for (int i = 1; i <= n; i++) { ans = max(ans, f[n][i]); } cout << ans; return 0; }
练习:数字三角形2
最长上升子序列:
运用线段树,区间询问最大值和单点修改
背包:背包九讲
01背包
完全背包
练习:
洛谷 1048
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<iomanip> #include<string> #include<algorithm> #include<cstdlib> using namespace std; int dp[10000000],v[1000],p[1000]; int main() { int n,m; cin>>n>>m; for(int a=1;a<=m;a++) { cin>>v[a]>>p[a]; } for(int j=1;j<=m;j++) { for(int i=n;i>=v[j];i--) { dp[i]=max(dp[i],dp[i-v[j]]+p[j]); } } cout<<dp[n]; return 0; }


