清北学堂培训2019.4.28
Day 1(冯哲)
今天的内容很杂但却都是基础知识
主要分为下面几个点
枚举
枚举也称作穷举,指的是从问题所有可能的解的集合中一一枚举各元素。用题目中给定的检验条件判定哪些是无用的,哪些是有用的。能使命题成立的即为其解。
有几个非常非常简单的例题:

这个题目类似于洛谷P1046 陶陶摘苹果
下放代码(不行不行太水了):
#include<iostream> #include<cstdio> using namespace std; int n,x,ans,s[101]; int main() { cin>>n>>x; for(int i=1;i<=n;i++) { cin>>s[i]; if(x>=s[i]) { ans++; } } cout<<ans; } /* //洛谷题解qwq #include<iostream> using namespace std; int n,s[10],ans; int main() { for(int i=0;i<10;i++) cin>>s[i]; cin>>n; for(int i=0;i<10;i++) if(n>=s[i]-30) ans++; cout<<ans; } */
还有就是有关素数判定最laji的方法
#include<iostream> using namespace std; int main() { int m; cin>>m; for(int i=2;i*i<=m;i++) { if(m%i==0) { cout<<"合数"; return 0; } } cout<<"素数"; }
没错,就是辣么的简单qwq【当然又双叒叕讲了筛法】



是个正常人都知道用哪个啊
还有就是有关枚举的优缺点:
优点:
- 简单明了,分析直观
- 能够帮助我们更好地理解问题
- 运用良好的枚举技巧可以使问题变得更简单
缺点
- 时空间效率低
- 往往没有利用题目中的特殊性质
- 产生了大量冗余状态
搜索
本质上是一种枚举,搜索算法一般做一些普通的枚举不方便表达状态的情况 。
例题:
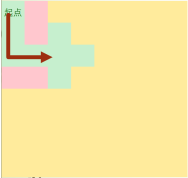
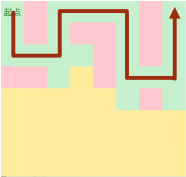
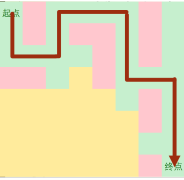
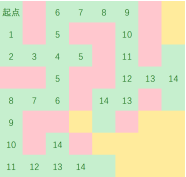
给出一个N*N的迷宫,求从起点出发,不经过障碍物到达终点的最短距离

解决这类问题一般有两种方式
1.深度优先搜索(DFS【大法师】)
2.广度优先搜索(BFS【笨法师】)
前置知识:
栈:后进先出的数据结构
支持的操作:
加入一个数
删除最晚加入的数
查询最晚加入的数
实现:一个数组+一个用于指向栈顶位置的变量
系统内部递归即使用了栈
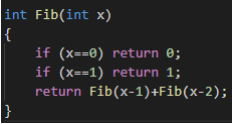
例如求斐波那契数列的第n项 :
队列:先进先出的数据结构
支持的操作:
加入一个数
删除最早加入的数
查询最早加入的数
实现:一个数组+头下标+尾下标
DFS的做法图解:
(a) (b) (c)
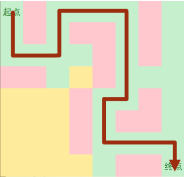
(d)
DFS:
优点:
- 占用空间小(只需要记录从起点到当前点的路径)
- 代码短
缺点:
- 获得的不一定是最优解
- 在图上路径非常多的时候,复杂度可能会达到指数级别
BFS的做法图解:
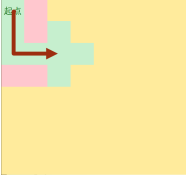
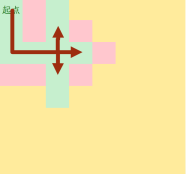

(a) (b) (c)

(d) (e)
BFS:
优点:
- 找到答案时找到的一定是最优解
- 复杂度不会超过图的大小
缺点:
- 需要维护一个“当前箭头的集合”
- 空间较大
BFS与DFS的区别:
- DFS:能走就走,走不了才回头(比较决绝)
- BFS:我全都要(要不是笨法师呢qwq)
应用:
G = (V , E)被称为一张图,则其包含两部分:
1.点集|V | = n,即有n个点,标号分别为1, 2, ..., n
2.边集|E| = m,有m条边(ui, vi),表示第ui个点和第vi个点有一条边相连.
边有向边和无向边之分,(u, v)是无向边,则u能直接走到v,v能直接走到u.
还有就是存图的问题:
有这么几种方法:
- 邻接矩阵存储,用A[x][y] = 0/1表示.优点是便于加删,但是需要O(N^2)的空间.
- 直接用vector存下所有的边(邻接表法).优点是空间和访问比较快,缺点是删除比较麻烦.
- 之前发的链式前向星
图的连通块
在本课中我们基本只考虑无向图.
若a沿着边走可以到b,则称a与b在同一个连通块中,称a与b连通.
显然a与b连通,b与c连通,则a与c肯定连通.
一张图可以被分成若干个两两连通的块.
这里就只放一个例题吧:
八数码游戏是一种非常无聊的游戏。给定一个3*3的格子,在其中8个格子中放置整数1 ∼ 8,
剩下一个格子空着(用0表示)。每次操作时,你可以选择将某个与空格相邻的数字移动到空
格上。给定一个初始局面,求最少需要多少次操作才能将局面变成
1 2 3
4 5 6
7 8 0
状态?0 ∼ 8 的一个排列
转移?一步能够到达的其他排列
BFS or DFS? BFS
按照这个思路,我们就能很好的得出答案:考虑倒着进行游戏过程。所有状态都是由
最终状态转移得到的因此我们以最终态为起点做一遍BFS即可预处理出所有状态的答案
贪心
每一步都取当前的最优解的思想;一般来说符合直观思路;
需要严格的证明;OI中使用多个错误的贪心策略进行加成有时会有良好的效果
例一
给定N个农民,第i个农民有Ai单位的牛奶,单价Pi;
现在要求从每个农民手中购买不超过Ai单位,总共M单位的牛奶。
求最小花费
(洛谷P1208 [USACO1.3]混合牛奶 Mixing Milk)
#include<bits/stdc++.h> using namespace std; #define N 5001 #define cmp zhx_ak_ioi//神仙保佑 int n,m,i,sum; struct node { int x,y; }a[N]; inline int cmp(node g,node c) { if(g.x!=c.x) { return g.x<c.x; } else { return g.y>c.y; } } int main() { cin>>m>>n; for(i=1;i<=n;i++) { cin>>a[i].x>>a[i].y; } sort(a+1,a+n+1,cmp); i=1; while(m) { if(a[i].y) { a[i].y--; sum+=a[i].x; m--; } else { i++; } } cout<<sum; }
二分
给定一个单调的函数/数组;给定一个值,求这个值是否存在;
或者找到这个值应当存在的位置
由于数组有序,不妨认为他单调递增
假设Ai > x,则必然有∀j > i, Aj > x
假设Aj < x,则必然有∀j < i, Aj < x
二分的原理就是每次在待定区间中选择mid。
必然可以确定一边是没有意义的。每次问题的规模缩小 12
因此复杂度为O(logN)
顾名思义,就是对答案进行二分
对于某些要求“满足某条件的最小值”类的问题,对答案进
行二分,假设答案不超过mid,则问题变为“满足某条件且
某值不超过mid”的判定性问题。
常用于最大值最小化类问题。
在二分答案之后往往需要一个贪心策略。
相对来说理解起来就简单了
分治
思想:将一个问题划分成若干个(一般都是分成俩)子问题分别解决每个子问题后(也可能是前,还可能一前一后之类的)
将各个子问题组合起来得到原问题的答案。
这里经典的就是快速幂了
归并排序
基本思想:先将整个数组分成两个部分,分别将两个部分排
好序,然后将两个排好序的数组O(n)合并成一个数组。
我们将问题分为两个阶段:分、治
分:
对于每个长度> 1的区间,拆成两个[l, mid]区间和[mid + 1, r]区间
直接递归下去
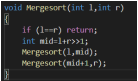
治:
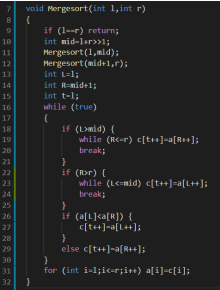
我们认为在处理区间[l,r]时,已经有[l,mid]和[mid+1,r]内分别有序
这一次的操作就是合并两个有序序列,成为一个新的长有序序列
用两个指针分别指向左右分别走到哪了即可
有关题目的链接:
搜索: 8数码 http://poj.org/problem?id=1077 走迷宫 http://poj.org/problem?id=3984 推箱子 http://acm.hdu.edu.cn/showproblem.php?pid=1254 贪心: 纪念品分组 洛谷P1094 例四:http://codeforces.com/contest/954/problem/E 例五:http://codeforces.com/contest/898/problem/D 二分: 跳石子:NOIP往年题,自行查找题库 例三 http://codeforces.com/contest/954/problem/G 三分 http://codeforces.com/contest/939/problem/E 分治: 平面最近点对:http://acm.hdu.edu.cn/showproblem.php?pid=1007 例二:http://codeforces.com/contest/768/problem/B 例一:http://codeforces.com/contest/97/problem/B