清北学堂培训2019.4.5
Day 2（今天是来自清华姚班的钟皓曦大佬）
（一堆数论的证明）
没错，主要是一些证明：
数论（初等）;研究整数性质的东西，所以理论上不会接触任何小数
这里包括一些基础性质
整除性：
设a, b ∈ ℤ，如果∃c∈ ℤ并且a = bc,则称b|a
称：
b为a的因子
b能整除a
a能被b整除
质数:
只有1和自身作为因子的数叫做质数
以𝜋(𝑥)表示不超过 x 的素数的个数，可以证
lim 𝜋(𝑥) ln x ÷ 𝑥 = 1
整数分解定理：
任何一个大于1的自然数
，如果N不为质数，都可以唯一分解成有限个质数的乘积
，这里
均为质数，其诸指数
是正整数。
PS:这里的证明十分玄学，先证明其存在性，再证明其唯一性：
存在性;
反证法
我们不妨假设存在最小的不满足条件的整数N，当N为质数时，显然不成立；当N为合数时，存在P，使得N=P*（N/P），因为N/P<N,与假设N为最小的矛盾，所以存在性就这么证完了；
大佬是这么说的：
假设N为最小的不满足条件的最小的数
若N为质数直接gg
若N为合数还是gg
证毕
唯一性:
还是反证
我们不妨假设存在最小的不满足条件的整数N（不想打了，直接上图）（钟皓曦大佬比较喜欢瞎搞）【锻炼我们的瞎搞能力】
（与存在性证明及其相似）
素数判定（O(sqrt(n)的算法——Miller-Rabin素性测试）
大体是这样的：若n为素数，我们取a<n;设n-1=d×2r,则要么ad≡1（mod n），要么存在0≤i<r,使得a的d×2i次方≡-1(mod n)【注意：只能有大部分的成立，因为其逆定理错误，这是素数的性质，而不代表有些毒瘤数不满足这样的性质】
钟皓曦大佬比较喜欢用2,3,5,7,13,29,37,89这八个数检查（据说这八个数在int范围内保证准确率100%)
大体的代码是这样的;
int gg[8] = {2,3,5,7,13,29,37,89}; bool miller_rabin(int a,int n) { int d=n-1,r=0; while (d%2==0) d/=2,r++; int x = kuaisumi(a,d,n); if (x==1) return true; for (int i=0;i<r;i++) { if (x==n-1) return true; x=(long long)x*x%n; } return false; } bool is_prime(int n) { if (n<=1) return false; for (int a=0;a<8;a++) if (n==gg[a]) return true; for (int a=0;a<8;a++) if (!miller_rabin(gg[a],n)) return false; return true; }
还有讲了n遍的筛法qwq
当然，还有大家熟悉的exgcd和裴蜀定理
（exgcd【扩展欧几里得】）
裴蜀定理：
同样是证明（不得使用唯一分解定理）：
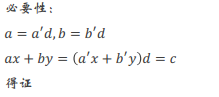
还有孙子定理qwq
分为正经做法和邪道做法
相信大家对于正经做法应该都知道
那就来说说钟皓曦小学学的邪道做法：
大数翻倍法qwq（别忘记降低自己的复杂的（据说钟皓曦大佬省一是靠这个方法出来的））
那个，打字太累，我之前写过的就先不写了（专挑重点写）
线性求逆元
还有BSGS算法（通过例题讲解）
int size; bool erfen(int x) { int l=0,r=size; while (l+1!=r) { int m=(l+r)>>1; if (z[m]>=x) r=m; else l=m; } return z[r]==x; } int bsgs(int a,int b,int p) { size = sqrt(p); int nowv=1; for (int i=1;i<=size;i++) { nowv = (long long)nowv * a%p; z[i] = nowv; if (z[i] == b) return i; } sort(z+1,z+size+1); for (int i=2;(i-1)*size+1 <= p;i++) { int y = (long long)b * kuaisumi(kuaisumi(a,size*(i-1),p),p-2,p); if (erfen(y)) { for (int j=(i-1)*size+1;j<=i*size;j++) if (kuaisimi(a,j,p) == b) return j; } } return -1; }
积性函数
积性函数：当gcd(a,b)=1时，ƒ(ab)=ƒ(a)ƒ(b)
完全积性函数：ƒ(ab)=f(a)f(b)
给一些积性函数：
不变函数：ƒ(n)=n
欧拉函数：ƒ(n)=φ(n)
莫比乌斯函数：ƒ(n)=μ(n)
因子数目总数：ƒ(n)=d(n)
因子之和函数：ƒ(n)=σ(n)
莫比乌斯函数的性质
莫比乌斯反演：
证明：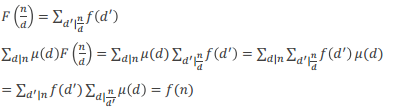
数论函数的卷积公式：
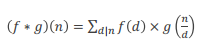
long long f[N],g[N],h[n]; void calc(int n) { for(int i=1;i*i<=n;i++) { h[i*i]+=f[i]*g[i]; for(int j=i+1;i*j<=n;j++) { h[i*j]+=f[i]*g[i]+f[i]*g[i]; } } }
这里貌似还有一个例子：
求当a≤x≤b,c≤y≤d时，gcd（x，y）=1的（x，y）的个数；
这里就需要用到卷积公式和前面的莫比乌斯反演以及积性函数的知识来进行一波推倒
核心代码如下：
xian_xing_shai(); for (int a=1;a<=n;a++) sum_mu[a] = sum_mu[a-1] + mu[a]; int solve(int n,int m) { int ans=0; //for (int d=1;d<=n;d++) // ans += mu[d] * (n/d) * (m/d); for (int d=1;d<=n;) { int next_d = min( n/(n/d), m/(m/d) ); ans += (sum_mu[next_d] - sum_mu[d-1]) * (n/d) * (m/d); d=next_d+1; } return ans; } //求当x大于等于a小于等于b，y大于等于c小于等于d时gcd（x，y）=1的个数
这一天简洁来说：浑浑噩噩
