浅析算法时间复杂度O(1)、O(n)、O(logn)、O(n^2)的理解

　　时间复杂度：按照我的理解，时间复杂度就是程序运行次数的数量级。

　　注意！时间复杂度不是单纯的耗时，而是指耗时与数据增长量之间的关系（一般可以套用耗时x数量增长量），我搜了下，竟然有“时间复杂度为O(1)就是耗时1秒，查找10000次时间复杂度O(n)就是耗时10000秒”这样扯淡的说法

一、时间复杂度O(1)理解：

　　常数阶O(1)：无论代码执行了多少行，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)

是最低的时空复杂度了，也就是耗时/耗空间与输入数据大小无关，无论输入数据增大多少倍，耗时/耗空间都不变。

哈希算法就是典型的O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到目标（不考虑冲突的话）

　　这个很简单，一般的简单操作就是O(1)，像 int n = 1 这样单步骤的（我称之为元操作），这个不需要多讲。

　　一般来说，像执行查找的时候，像HashMap这样通过 contains() 方法查找HashCode直接可以查找出某个值的操作，其时间复杂度也是O(1)。

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

　　上述代码在执行的时候，它消耗的时候并不随着某个变量的增长而增长，那么无论这类代码有多长，即使有几万几十万行，都可以用O(1)来表示它的时间复杂度。

二、时间复杂度O(n)理解：

　　线性阶O(n)：它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度。

for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

　　这段代码，for循环里面的代码会执行n遍，因此它消耗的时间是随着n的变化而变化的，因此这类代码都可以用O(n)来表示它的时间复杂度。

就代表数据量增大几倍，耗时也增大几倍

比如常见的遍历算法。再比如时间复杂度O(n^2)，就代表数据量增大n倍时，耗时增大n的平方倍，这是比线性更高的时间复杂度。比如冒泡排序，就是典型的O(n^2)的算法，对n个数排序，需要扫描n×n次。

　　这里用使用contains()方法使用查找List集合里面的某个元素来举例。

　　List是有序表，不能直接一次性查找到。比如从 {12，23，45，··· ···，76，32} 里面查找76，要从12开始查找，一次次循环查找，直到查到76并返回。

　　这里每次的查找时间复杂度为O(1)，需要查找N次才能查到76，则时间复杂度可以看作是 N * O(1)=O(n)。

　　注意，这里的n不是具体的数值N，不要以为查询了100次就是O(100)，这是错的，这里只是为了方便理解（前面说了，时间复杂度并不是单指耗时，下同）。

三、时间复杂度O(logn)理解：

　　对数阶O(logN)

int i = 1;
while(i<n){
    i = i * 2;
}

　　从上面代码可以看到，在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2^n。也就是说当循环 log2^n 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O(logn)

当数据增大n倍时，耗时增大logn倍（这里的log是以2为底的，比如当数据增大256倍时，耗时只增大8倍，是比线性还要低的时间复杂度）。
二分查找就是O(logn)的算法，每找一次排除一半的可能，256个数据中查找只要找8次就可以找到目标。

1、一般的查找都是 O(n)，但是如果通过算法，可以使查找的时间复杂度降低，比如二分查找。

　　像上面解释 O(n) 的例子中，采用二分查找的话，是不是就是个 log(O(n)) 的对数数学模型，所以其时间复杂度为O(logn)。

2、时间复杂度为O(nlogn)就是n乘以logn，当数据增大256倍时，耗时增大256*8=2048倍。这个复杂度高于线性低于平方。归并排序就是O(nlogn)的时间复杂度。

四、线性对数阶O(nlogN)

　　线性对数阶O(nlogN) 其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。就拿上面的代码加一点修改来举例：

for(m=1; m<n; m++){
    i = 1;
    while(i<n){
        i = i * 2;
    }
}

五、时间复杂度O(n^2)理解：

　　平方阶O(n²) 就更容易理解了，如果把 O(n) 的代码再嵌套循环一遍，它的时间复杂度就是 O(n²) 了。举例：

for(x=1; i<=n; x++){
   for(i=1; i<=n; i++){
       j = i;
       j++;
    }
}

　　这段代码其实就是嵌套了2层n循环，它的时间复杂度就是 O(n*n)，即 O(n²) 。如果将其中一层循环的n改成m，即：

for(x=1; i<=m; x++){
   for(i=1; i<=n; i++){
       j = i;
       j++;
    }
}

　　那它的时间复杂度就变成了 O(m*n)。

　　这里拿冒泡排序对某个数组进行有序排序举例。

　　在冒泡排序中，分为获取值、对该值进行排序、重复取值排序三个步骤。

　　其中取值时间复杂度为O(1)，则在N个数中进行该值的比较排序，则为N*O(1)=O(n)时间复杂度。

　　这时候还没有获取到有序数组，必须对这N个数重复进行取值、排序，执行N次，故时间复杂度为 N * N * O(1)=O(n^2)。

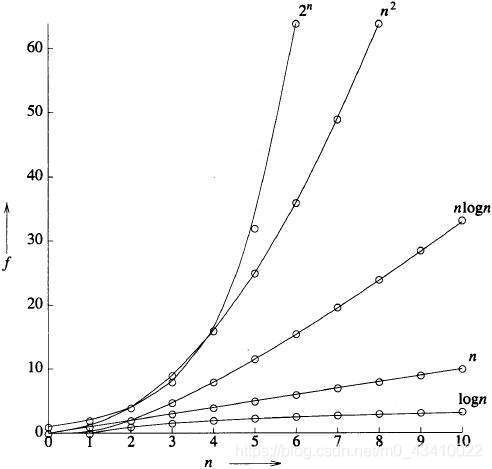
六、常用排序方式的复杂度：各种时间复杂度下随操作量级N增长耗时，从中可以知道二分查找的魅力