浅析什么是哈希算法/散列函数/哈希函数
一、什么是 hash
Hash(哈希),又称“散列”。散列(hash)英文原意是“混杂”、“拼凑”、“重新表述”的意思。
在某种程度上,散列是与排序相反的一种操作,排序是将集合中的元素按照某种方式比如字典顺序排列在一起,而散列通过计算哈希值,打破元素之间原有的关系,使集合中的元素按照散列函数的分类进行排列。
在介绍一些集合时,我们总强调需要重写某个类的 equlas() 方法和 hashCode() 方法,确保唯一性。这里的 hashCode() 表示的是对当前对象的唯一标示。计算 hashCode 的过程就称作 哈希。
二、为什么要有 Hash
我们通常使用数组或者链表来存储元素,一旦存储的内容数量特别多,需要占用很大的空间,而且在查找某个元素是否存在的过程中,数组和链表都需要挨个循环比较,而通过 哈希 计算,可以大大减少比较次数。
举个栗子:现在有 4 个数 {2,5,9,13},需要查找 13 是否存在。
1、使用数组存储,需要新建个数组 new int[]{2,5,9,13},然后需要写个循环遍历查找。
这样需要遍历 4 次才能找到,时间复杂度为 O(n)。
2、而假如存储时先使用哈希函数进行计算,这里我随便用个函数:
H[key] = key % 3;
// 四个数 {2,5,9,13} 对应的哈希值为:
H[2] = 2 % 3 = 2;
H[5] = 5 % 3 = 2;
H[9] = 9 % 3 = 0;
H[13] = 13 % 3 = 1;
然后把它们存储到对应的位置。当要查找 13 时,只要先使用哈希函数计算它的位置,然后去那个位置查看是否存在就好了,本例中只需查找一次,时间复杂度为 O(1)。
因此可以发现,哈希其实是随机存储的一种优化,先进行分类,然后查找时按照这个对象的分类去找。哈希通过一次计算大幅度缩小查找范围,自然比从全部数据里查找速度要快。比如你和我一样是个剁手族买书狂,家里书一大堆,如果书存放时不分类直接摆到书架上(数组存储),找某本书时可能需要脑袋从左往右从上往下转好几圈才能发现;如果存放时按照类别分开放,技术书、小说、文学等等分开(按照某种哈希函数计算),找书时只要从它对应的分类里找,自然省事多了。
三、什么是哈希算法
举个例子,比如这里有一万首歌,给你一首新的歌X,要求你确认这首歌是否在那一万首歌之内。无疑,将一万首歌一个一个比对非常慢。但如果存在一种方式,能将一万首歌的每首数据浓缩到一个数字(称为哈希码)中,于是得到一万个数字,那么用同样的算法计算新的歌X的编码,看看歌X的编码是否在之前那一万个数字中,就能知道歌X是否在那一万首歌中。
作为例子,如果要你组织那一万首歌,一个简单的哈希算法就是让歌曲所占硬盘的字节数作为哈希码。这样的话,你可以让一万首歌“按照大小排序”,然后遇到一首新的歌,只要看看新的歌的字节数是否和已有的一万首歌中的某一首的字节数相同,就知道新的歌是否在那一万首歌之内了。
当然这个简单的哈希算法很容易出现两者同样大小的歌曲,这就是发送了碰撞。而好的哈希算法发生碰撞的几率非常小。
解决碰撞是一个复杂问题。碰撞主要取决于:
1、散列函数,一个好的散列函数的值应尽可能平均分布。
2、处理碰撞方法。
3、负载因子的大小。太大不一定就好,并且浪费空间严重,负载因子和散列函数是联动的。
四、经常使用的哈希函数
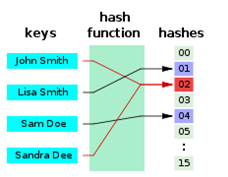
哈希的过程中需要使用哈希函数进行计算。哈希函数是一种映射关系,根据数据的关键词 key ,通过一定的函数关系,计算出该元素存储位置的函数。表示为:address = H [key]
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。
几种常见的哈希函数(散列函数)构造方法:
1、直接寻址法:取keyword或keyword的某个线性函数值为散列地址。即H(key)=key或H(key) = a•key + b,当中a和b为常数(这样的散列函数叫做自身函数)
2、数字分析法:分析一组数据,比方一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体同样,这种话,出现冲突的几率就会非常大,可是我们发现年月日的后几位表示月份和详细日期的数字区别非常大,假设用后面的数字来构成散列地址,则冲突的几率会明显减少。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3、平方取中法:取keyword平方后的中间几位作为散列地址。
4、折叠法:将keyword切割成位数同样的几部分,最后一部分位数能够不同,然后取这几部分的叠加和(去除进位)作为散列地址。
5、随机数法:选择一随机函数,取keyword的随机值作为散列地址,通经常使用于keyword长度不同的场合。
6、除留余数法:取keyword被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p, p<=m。不仅能够对keyword直接取模,也可在折叠、平方取中等运算之后取模。对p的选择非常重要,一般取素数或m,若p选的不好,easy产生同义词。
五、哈希函数原理
哈希函数不是指某种特定的函数,而是一类函数,它有各种各样的实现。
百度百科给出的定义是:
Hash,一般翻译做"散列",也有直接音译为"哈希"的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。
维基百科则直接将哈希函数的词条重定向到散列函数中,定义如下:
散列函数(英语:Hash function)又称散列算法、哈希函数,是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(hash values,hash codes,hash sums,或hashes)的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。
-
定义里面讲的是哈希函数接收任意长度的输入,但在实际实现中,大家都会指明一个具体可接收的阈值,例如SHA-2最高接受(2^64-1)/8长度的字节字符串。此处需要理解的是哈希函数拥有较为庞大的输入值域,它接受长度非常长的输入值。
-
产生固定长度的输出值。
-
不可逆性,已知哈希函数 fn 与 x 的哈希值无法反向求出 x,当然这里的不可逆是指计算上行不通,正着算很好算,反着算在当前的计算机计算能力条件下做不到。
-
对于特定的哈希函数,只要输入值不变,那么输出的值也是唯一不变的。
-
哈希函数的计算时间不应过长,即通过输入值求出输出值的时间不宜过长。
-
无冲突性,即对于输入值x,与哈希函数fn,无法求出一个值y,使得x与y的哈希值相等。但是由于上文我们知道,由于哈希函数实际上代表着一种映射(对应关系),将一个大区间上的数值映射到一个小区间上,它一定是有冲突的,这里的无冲突同样是指“求冲突在计算上行不通”,正向地计算很容易,但是反向的计算在当前的计算机能力条件下做不到,但是这种冲突的概率发生了怎么办我们后面再说。
-
即使修改了输入值的一个比特位,也会使得输出值发送巨大的变化。
-
哈希函数产生的映射应当保持均匀,即不要使得映射结果堆积在小区间的某一块区域。
为了方便理解,我们还是来举一个例子:手机电话簿我们都知道,里面的人名依据首字母从a-z的顺序排列着的,这种排列方式能让我们快速地找到某个人。
我们不妨认定这种映射过程为一个简陋的哈希函数,并称这个简陋的哈希函数为“电话簿哈希”。我们可以看到,“电话簿哈希”的运行机制很简单:对于任意输入值,“电话簿哈希”都取第一个字的拼音首字母输出。
这个哈希函数实际上满足我们在上方列举的8条属性中的前5条的。但是从第6条开始,我们定义的这个电话簿哈希就不满足了。
我们来分析一下,由于这个这个函数过于简陋,它的冲突概率是较高的,比如我们分别输入“张三”、“章五”,“电话簿哈希”都输出了“z”,对于这种冲突,在哈希函数具体实现中处理方法有多种,例如“链地址法”、“再哈希法”等,文章也有很多,需要理解的是为啥它们要这么做,好处都有啥,此处不谈。
回到我们的电话簿哈希中,针对此处的冲突我们修改一下哈希函数:“将取第一个字的首字母改为取每个字的首字母”。也就是说输入“张三”与“章五”输出值变成了“zs”与“zw”,之后我们再来通过输出值执行名字到电话簿位置的映射。
存放到具体位置遵循以下规则,定位依然遵循从a到z的顺序,但是出现冲突后取第二个字的首字母再排序。那么咱们这个升级后的“电话簿哈希”对于上方的输入,就有了更为具体的电话簿位置映射。
此时,“张三”与“章五”无需冲突在位置“z”上,而是在位置“z”上冲突后,执行了冲突解决方法,即以第二个字首字母对冲突对象再排序,“s”排在“w”之前,因此,“张三”与“章五”应当排在电话簿的“z”下,且“张三”的位置在“章五”前面。
但是这个升级后的哈希函数依然有漏洞,它还有冲突未解决,但是此处主要为了说清楚哈希函数解决冲突的一个大致套路与思想,这个哈希函数的漏洞由读者(然而一个读者也没有)自行发掘,不妨碍此处的说明。
即使我们已完美解决了冲突的问题,但是回顾咱们“电话簿哈希”这个哈希函数的设计原理,咱们的电话簿哈希依然存在问题——假设我姓“刘”,那么由于我会保存很多姓“刘”的亲戚,电话簿中大量的联系人都映射在了“L”这个地址下。
即使我们有了升级版的解决办法,能解决冲突的问题,但是由于映射的不均匀,大量的数据堆积在了一块区域,那么冲突发生的概率顿时就高了许多。由此导致本来查找速度极快的哈希函数速度降下来许多了——因为它需要继续执行冲突之后的遍历。这个与现实生活中的体验是一致的:我们能通过一次查找定位人名在“L”下,但是我们要具体找到目标甚至需要遍历“L”下挂着的所有对象,这是一个优秀的哈希函数所难以容忍的。
我们的哈希函数“电话簿哈希”还需要升级,使得映射能够更均匀一些。这里就不再继续开脑洞如何升级“电话簿哈希”这个函数了。但是需要说明的是,就算我们将来能解决这个映射不均匀的问题,我们也会引入一个新的问题:这个哈希函数计算起来变复杂了,它为了兼顾前文我们列举的种种要求种种属性,函数考虑的东西越来越多应对的情况越来越丰富,以至于函数本身体积膨胀,计算哈希值(输出值)变的很耗费CPU(脑细胞)。
试想,我们发明这个哈希函数目的就是为了快点找到目标人名,但是在找到这个人名之前我们得经过一系列的计算,那岂不是违背设计这个函数以达到“快速查找”的初衷。所以这里往往要做一个权衡,实际上很多类似的函数设计都有这个权衡在里面。
手机中的电话簿实现到了这一步基本就停止了,没有再去解决映射不均匀的情况实际上也是权衡的结果。人脑根据拼音首字母来定位到特定字母目录下,而不用遍历一整个电话簿已经帮了很大忙了,而且人脑完成这一映射的速度也非常快(计算简单),所需要的仅仅是费些时间遍历某个字母下挂靠着的节点而已。
哈希函数的通俗说明到这里已经说的差不多了,上文列举了哈希函数所具备的属性,也通过一个通俗的例子来辅助理解了哈希函数的种种属性与用于“快速查找”的应用场景。哈希函数十分强大,除了上文的“快速查找”场景以外,还有许多经典的场景。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号