浅析深度优先和广度优先遍历实现过程、区别及使用场景
一、什么是 深度/广度 优先遍历?
深度优先遍历简称DFS(Depth First Search),广度优先遍历简称BFS(Breadth First Search),它们是遍历图当中所有顶点的两种方式。
这两种遍历方式有什么不同呢?我们来举个栗子:
我们来到一个游乐场,游乐场里有11个景点。我们从景点0开始,要玩遍游乐场的所有景点,可以有什么样的游玩次序呢?
1、深度优先遍历
第一种是一头扎到底的玩法。我们选择一条支路,尽可能不断地深入,如果遇到死路就往回退,回退过程中如果遇到没探索过的支路,就进入该支路继续深入。 在图中,我们首先选择景点1的这条路,继续深入到景点7、景点8,终于发现走不动了:
于是,我们退回到景点7,然后探索景点10,又走到了死胡同。于是,退回到景点1,探索景点9:
按照这个思路,我们再退回到景点0,后续依次探索景点2、3、5、4、发现相邻的都玩过了,再回退到3,再接着玩6,终于玩遍了整个游乐场:
具体次序如下图,景点旁边的数字代表探索次序。当然还可以有别的排法。
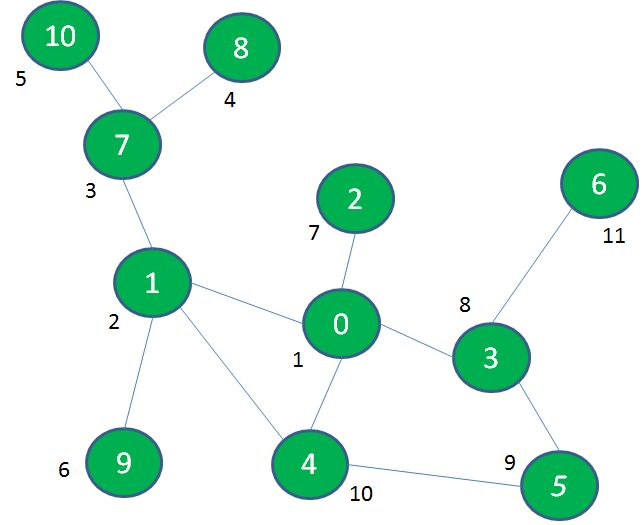
像这样先深入探索,走到头再回退寻找其他出路的遍历方式,就叫做深度优先遍历(DFS)。
这方式看起来很像二叉树的前序遍历。没错,其实二叉树的前序、中序、后序遍历,本质上也可以认为是深度优先遍历。
2、广度优先遍历
除了像深度优先遍历这样一头扎到底的玩法以外,我们还有另一种玩法:首先把起点相邻的几个景点玩遍,然后去玩距离起点稍远一些(隔一层)的景点,然后再去玩距离起点更远一些(隔两层)的景点…
在图中,我们首先探索景点0的相邻景点1、2、3、4:
接着,我们探索与景点0相隔一层的景点7、9、5、6:
最后,我们探索与景点0相隔两层的景点8、10:

像这样一层一层由内而外的遍历方式,就叫做广度优先遍历(BFS)。
这方式看起来很像二叉树的层序遍历。没错,其实二叉树的层序遍历,本质上也可以认为是广度优先遍历。
二、深度/广度优先遍历 的实现
那么我们如何来实现图的深度优先和广度优先遍历的算法呢?
实现深度优先遍历的关键在于【回溯】;实现广度优先遍历的关键在于【重放】。下面我们来演示一下两种算法的实现过程。
1、深度优先遍历实现
首先说说深度优先遍历的实现过程。这里所说的回溯是什么意思呢?回溯顾名思义,就是自后向前,追溯曾经走过的路径。
我们把刚才游乐场的例子抽象成数据结构的图,假如我们依次访问了顶点0、1、7、8,发现无路可走了,这时候我们要从顶点8退回到顶点7。
而后我们探索了顶点10,又无路可走了,这时候我们要从顶点10退回到顶点7,再退回到顶点1。
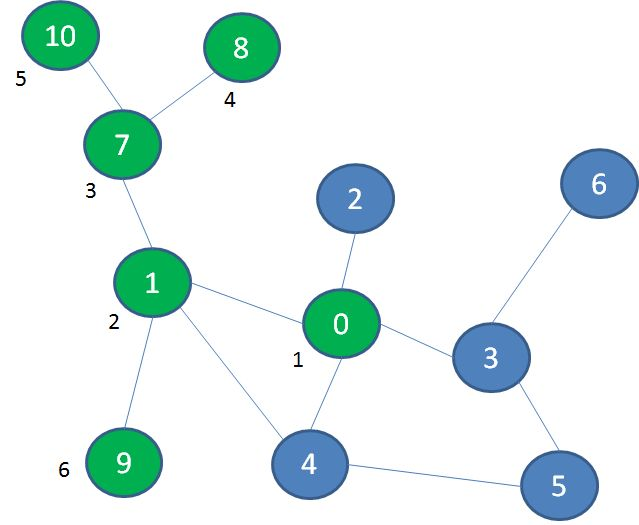
像这样的自后向前追溯曾经访问过的路径,就叫做回溯。
要想实现回溯,可以利用栈的先入后出特性,也可以采用递归的方式(因为递归本身就是基于方法调用栈来实现)。
下面我们来演示一下具体实现过程。
首先访问顶点0、1、7、8,这四个顶点依次入栈,此时顶点8是栈顶:
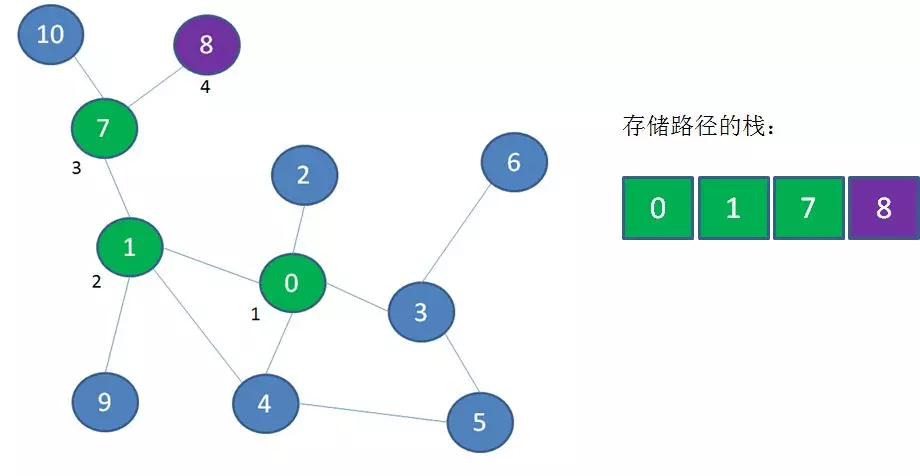
从顶点8退回到顶点7,顶点8出栈 —— 存储路径的栈:0-1-7
接下来访问顶点10,顶点10入栈 —— 存储路径的栈:0-1-7-10
从顶点10退到顶点7,从顶点7退到顶点1,顶点10和顶点7出栈 —— 存储路径的栈:0-1
探索顶点9,顶点9入栈 —— 存储路径的栈:0-1-9
以此类推,利用这样一个临时栈来实现回溯,最终遍历完所有顶点。
2、广度优先遍历实现
接下来该说说广度优先遍历的实现过程了。刚才所说的重放是什么意思呢?似乎听起来和回溯差不多?其实,回溯与重放是完全相反的过程。
仍然以刚才的图为例,按照广度优先遍历的思想,我们首先遍历顶点0,然后遍历了邻近顶点1、2、3、4:
接下来我们要遍历更外围的顶点,可是如何找到这些更外围的顶点呢?我们需要把刚才遍历过的顶点1、2、3、4按顺序重新回顾一遍,从顶点1发现邻近的顶点7、9;从顶点3发现邻近的顶点5、6。

像这样把遍历过的顶点按照之前的遍历顺序重新回顾,就叫做重放。同样的,要实现重放也需要额外的存储空间,可以利用队列的先入先出特性来实现。
下面我们来演示一下具体实现过程。
首先遍历起点顶点0,顶点0入队 —— 遍历队列:0
接下来顶点0出队,遍历顶点0的邻近顶点1、2、3、4,并且把它们入队 —— 遍历队列:1-2-3-4

然后顶点1出队,遍历顶点1的邻近顶点7、9,并且把它们入队 —— 遍历队列:2-3-4-7-9(1出队,1的邻近点7-9)
然后顶点2出队,没有新的顶点可入队 —— 遍历队列:3-4-7-9(1出队,1的邻近点7-9)
以此类推,利用这样一个队列来实现重放,最终遍历完所有顶点。
3、代码实现
无论是深度优先遍历还是广度优先遍历,当我获取一个顶点若干相邻顶点时,我该如何判断这个顶点有没有被访问过呢?
这个问题提的很好,我们可以利用一个数组来存储所有顶点的访问状态。顶点对应元素的初始值都是false,代表未遍历,遍历之后就变为true。
下面我们来看一下深度优先遍历和广度优先遍历的完整代码实现:
// 图的顶点
private static class Vertex {
int data;
Vertex( int data) {
this.data = data;
}
}
// 图(邻接表形式)
private static class Graph{
private int size;
private Vertex[] vertexes;
private LinkedList<Integer> adj[];
Graph(int size){
this.size = size;
//初始化顶点和邻接矩阵
vertexes = new Vertex[size];
adj = new LinkedList[size];
for(int i=0; i<size; i++){
vertexes[i] = new Vertex(i);
adj[i] = new LinkedList();
}
}
}
// 深度优先遍历
public static void dfs(Graph graph, int start, boolean[] visited) {
System.out.println(graph.vertexes[start].data);
visited[start] = true;
for(int index : graph.adj[start]){
if(!visited[index]){
dfs(graph, index, visited);
}
}
}
// 广度优先遍历
public static void bfs(Graph graph, int start, boolean[] visited, LinkedList<Integer> queue) {
queue.offer(start);
while (!queue.isEmpty()){
int front = queue.poll();
if(visited[front]){
continue;
}
System.out.println(graph.vertexes[front].data);
visited[front] = true;
for(int index : graph.adj[front]){
queue.offer(index);;
}
}
}
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.adj[0].add(1);
graph.adj[0].add(2);
graph.adj[0].add(3);
graph.adj[1].add(0);
graph.adj[1].add(3);
graph.adj[1].add(4);
graph.adj[2].add(0);
graph.adj[3].add(0);
graph.adj[3].add(1);
graph.adj[3].add(4);
graph.adj[3].add(5);
graph.adj[4].add(1);
graph.adj[4].add(3);
graph.adj[4].add(5);
graph.adj[5].add(3);
graph.adj[5].add(4);
System.out.println("图的深度优先遍历:");
dfs(graph, 0, newboolean[graph.size]);
System.out.println("图的广度优先遍历:");
bfs(graph, 0, newboolean[graph.size], newLinkedList<Integer>());
}
三、深度优先与广度优先遍历区别对比
1、二叉树的深度优先遍历的非递归的通用做法是采用栈,广度优先遍历的非递归的通用做法是采用队列。
2、深度优先遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。要特别注意的是,二叉树的深度优先遍历比较特殊,可以细分为先序遍历、中序遍历、后序遍历。具体说明如下:
- 先序遍历:对任一子树,先访问根,然后遍历其左子树,最后遍历其右子树。
- 中序遍历:对任一子树,先遍历其左子树,然后访问根,最后遍历其右子树。
- 后序遍历:对任一子树,先遍历其左子树,然后遍历其右子树,最后访问根。
3、广度优先遍历:又叫层次遍历,从上往下对每一层依次访问,在每一层中,从左往右(也可以从右往左)访问结点,访问完一层就进入下一层,直到没有结点可以访问为止。
4、深度优先搜素算法:不全部保留结点,占用空间少;有回溯操作(即有入栈、出栈操作),运行速度慢。—— 储存空间小,运行慢
5、广度优先搜索算法:保留全部结点,占用空间大; 无回溯操作(即无入栈、出栈操作),运行速度快。—— 存储空间大,运行快
通常深度优先搜索法不全部保留结点,扩展完的结点从数据库中弹出删去,这样,一般在数据库中存储的结点数就是深度值,因此它占用空间较少。所以,当搜索树的结点较多,用其它方法易产生内存溢出时,深度优先搜索不失为一种有效的求解方法。
广度优先搜索算法,一般需存储产生的所有结点,占用的存储空间要比深度优先搜索大得多,因此,程序设计中,必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作,即入栈和出栈的操作,所以运行速度比深度优先搜索要快些。
6、最后我们来看一个图,写一下搜索步骤:
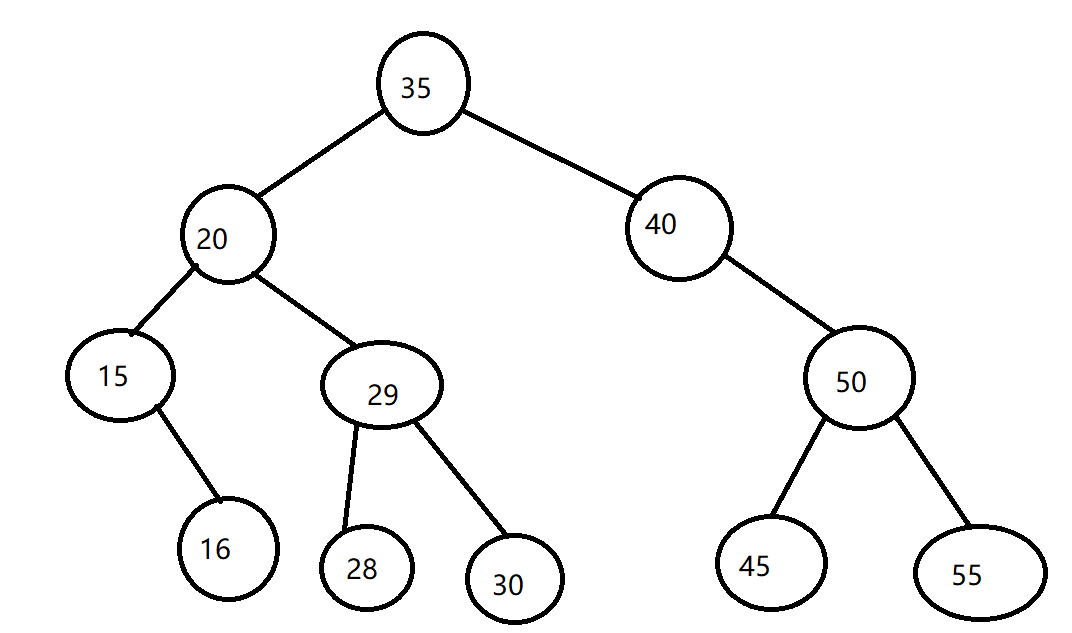
(1)深度优先遍历:
前序遍历:35,20,15,16,29,28,30,40,50,45,55
中序遍历:15,16,20,28,29,30,35,40,45,50,55
后序遍历:16,15,28,30,29,20,45,55,50,40,35
(2)广度优先遍历:35 20 40 15 29 50 16 28 30 45 55
四、什么时候使用深度优先遍历?什么时候使用广度优先遍历?
我理解DFS和BFS之间的区别,但是我很想知道何时使用一个比另一个更实用?
比较BFS和DFS,DFS的一大优势是它比BFS具有更低的内存要求,因为没有必要在每个级别存储所有子指针。根据数据和您要查找的内容,DFS或BFS可能是有利的。
这在很大程度上取决于搜索树的结构以及解决方案的数量和位置(也就是搜索项目)。
- 如果您知道解决方案离树的根不远,那么广度优先搜索(BFS)可能会更好。
-
如果树很深并且解决方案很少,深度优先搜索(DFS)可能需要很长时间,但BFS可能会更快。
-
如果树很宽,BFS可能需要太多内存,所以它可能完全不切实际。
-
如果解决方案频繁但位于树的深处,那么BFS可能是不切实际的。
- 如果搜索树非常深,则无论如何都需要限制深度优先搜索(DFS)的搜索深度(例如,使用迭代加深)。
但这些只是经验法则; 你可能需要进行实验。
1、深度优先搜索
深度优先搜索通常用于模拟游戏(以及现实世界中类似游戏的情况)。 在典型的游戏中,您可以选择几种可能的操作之一。 每种选择都会导致进一步的选择,每种选择都会导致进一步的选择,以此类推,形成一种不断扩展的树形可能性图。
例如在像国际象棋这样的游戏中,当你决定做出什么样的动作时,你可以在心理上想象一个动作,然后你的对手的可能反应,然后是你的反应,等等。 您可以通过查看哪种移动可以获得最佳结果来决定做什么。
只有游戏树中的某些路径才能赢得胜利。 有些会导致你的对手获胜,当你达到这样的结局时,你必须备份或回溯到前一个节点并尝试不同的路径。 通过这种方式,您可以探索树,直到找到成功结束的路径。 然后沿着这条路径前进。
2、广度优先搜索
广度优先搜索具有一个有趣的属性:它首先找到距起点一个边缘的所有顶点,然后是两个边缘的所有顶点,依此类推。
如果您试图找到从起始顶点到给定顶点的最短路径,这将非常有用。 您启动BFS,当您找到指定的顶点时,您知道到目前为止您已跟踪的路径是该节点的最短路径。 如果路径较短,BFS就已经找到了。
广度优先搜索可用于在像对等网络中找到邻居节点,如BitTorrent,用于查找附近位置的GPS系统,用于查找指定距离内的人的社交网站以及类似的东西。
3、当树的深度可以变化时,广度优先搜索通常是最好的方法,并且您只需要搜索树的一部分以获得解决方案。 例如,找到从起始值到最终值的最短路径是使用BFS的好地方。
当您需要搜索整个树时,通常会使用深度优先搜索。 它比BFS更容易实现(使用递归),并且需要更少的状态:虽然BFS要求您存储整个“前沿”,但DFS只需要存储当前元素的父节点列表。
DFS比BFS更节省空间,但可能会达到不必要的深度。
参考文章:https://mp.weixin.qq.com/s/WA5hQXkcACIarcdVnRnuiw


