泰勒展开和麦克劳林级数

 

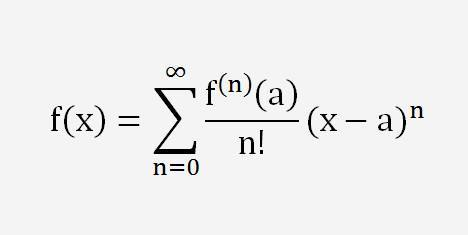
泰勒展开式真是个好东西，可以很方便的把一个函数展开成幂级数。当上图中a=0时，称麦克劳林级数。

（泰克展开可用积分证明，详见百度）

 

几个例子:

e^x=1 + x + x²/2！ + x³/3！+...

cosx　   = 1- (x²/2!) + (x⁴/4!) - (x⁶/6!) + ...

sinx　　= x - (x³/3!) + (x⁵/5!) - (x⁷/7!) + ...

设x=iz  ，由上3式可得：

e^iz = cosz + i*sinz

当z=Π 时（180度的弧度pai）

e^iΠ +1 =0