正态分布样本均值和样本方差的独立性证明

我们经常在数理统计的书上看到2个一笔带过的结论：

　　正态分布下：1. 样本均值和样本方差独立     

　　　　　　　　 2.  (n-1)S²/σ² ~ Χ²(n-1)   　

很多人都会对这2个结论产生疑问:

　　1).均值和方差都是由X₁,...X_n构成，看起来明显有关系，怎么会独立呢？

　　2).一般的解释为有一个约束条件所以减1,到底怎么界定这个约束条件?

问题其实都是可以证明的，过程如下:

　　设X₁,...X_n独立同分布且服从正态分布N(μ,σ²)

　　构造正交矩阵A

　　令Y=AX

　　E(Y)=E(AX)=AE(X)=(n^1/2μ,0,...,0)

　　Y^TY=(AX)^TAX=X^TA^TAX=X^TX

　　

 

 

 　　

　　

　　

 

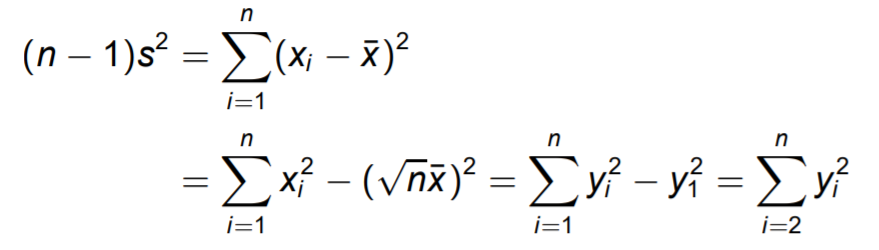
　　 (n-1)S²/σ² ~ Χ²(n-1)