算法
一. 时间复杂度
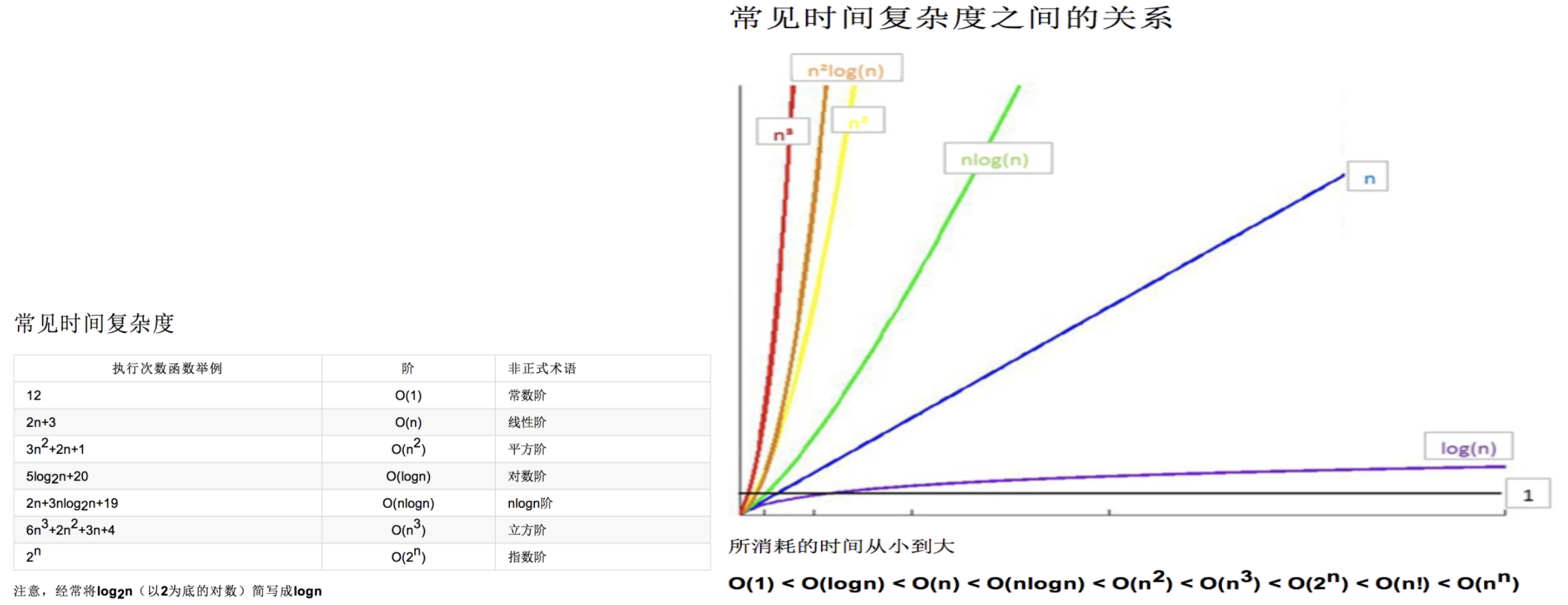
#在计算机科学中，算法的时间复杂度是一个函数，它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。 时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。 #时间复杂度是用来估计算法运行时间的一个式子(单位) #如何一眼判断时间复杂度? - 循环减半的过程->O(logn) - 几次循环就是n的几次方的复杂度
#时间复杂度 - 最优时间复杂度 - 最坏时间复杂度 - 平均时间复杂度 #时间复杂度的几条计算规则 - 基本操作 即只有常数项,认为其时间复杂度为O(1) - 顺序结构 时间复杂度按加法进行计算 - 循环结构 时间复杂度按乘法进行计算 - 分支结构 时间复杂度取最大值 - 判断一个算法的效率时, 往往只需要关注操作数量的最高次项, 其它次要项和常数项可以忽略 - 在没有特殊说明时,我们分析的算法的时间复杂度都是指最坏时间复杂度
a. 测试
# coding:utf-8 from timeit import Timer # li1 = [1, 2] # # li2 = [23,5] # # li = li1+li2 # # li = [i for i in range(10000)] # # li = list(range(10000)) def t1(): li = [] for i in range(10000): li.append(i) def t2(): li = [] for i in range(10000): li += [i] def t3(): li = [i for i in range(10000)] def t4(): li = list(range(10000)) def t5(): li = [] for i in range(10000): li.extend([i]) timer1 = Timer("t1()", "from __main__ import t1") print("append:", timer1.timeit(1000)) timer2 = Timer("t2()", "from __main__ import t2") print("+:", timer2.timeit(1000)) timer3 = Timer("t3()", "from __main__ import t3") print("[i for i in range]:", timer3.timeit(1000)) timer4 = Timer("t4()", "from __main__ import t4") print("list(range()):", timer4.timeit(1000)) timer5 = Timer("t5()", "from __main__ import t5") print("extend:", timer5.timeit(1000)) def t6(): li = [] for i in range(10000): li.append(i) def t7(): li = [] for i in range(10000): li.insert(0, i) #------------------结果------- append: 1.0916136799496599 +: 1.0893132810015231 [i for i in range]: 0.4821193260140717 list(range()): 0.2702883669990115 extend: 1.576017125044018
def t6(): li = [] for i in range(10000): li.append(i) def t7(): li = [] for i in range(10000): li.insert(0, i) timer6 = Timer("t6()", "from __main__ import t6") print("append", timer6.timeit(1000)) timer7 = Timer("t7()", "from __main__ import t7") print("insert(0)", timer7.timeit(1000)) #################### append 1.1599015080137178 insert(0) 23.26370093098376
b. 二分法
import random n = 10000 li = list(range(n)) def bin_search(li,val): low = 0 high = len(li) - 1 while low <= high: mid = (low + high) // 2 if li[mid] == val: return mid elif li[mid] < val: low = mid + 1 else: high = mid - 1 return None obj = bin_search(li,5550) print(obj)
# 习题 https://leetcode.com/problems/two-sum/description/ #方式一: def two_sum(li,target): l = len(li) for i in range(l): for j in range(i+1,l): if li[i] + li[j] == target: return (i,j) return None obj = two_sum([2,7,11,15],18) print(obj) #方式二: def bin_search(data_set, value): low = 0 high = len(data_set) - 1 while low <= high: mid = (low + high) // 2 if data_set[mid] == value: return mid elif data_set[mid] > value: high = mid - 1 else: low = mid + 1 def two_sum2(li, target): li.sort() for i in range(len(li)): b = target - li[i] j = bin_search(li, b) if j != None and i != j: return i, j obj = two_sum2([2, 7, 11, 15], 18) print(obj) #方式三: def two_sum3(li,target): li.sort() i = 0 j = len(li) - 1 while i < j: sum = li[i] + li[j] if sum > target: j-=1 elif sum < target: i+=1 else: return (i,j) return None obj = two_sum3([2,7,11,15],18) print(obj)
c. 排序
#排序low B三人组 - 冒泡排序 - 选择排序 - 插入排序 #快速排序 #排序NB二人组 - 堆排序 - 归并排序 #么人用的排序 - 基数排序 - 希尔排序 - 桶排序
#冒泡排序 - 列表每相邻的数,如果前边的比后边的大,那么交换这两个数 - 算法复杂度 n^2 import random def bubble_sort(li): for i in range(len(li) - 1): # i 趟 for j in range(len(li) - i -1): # j 指针 if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] return li li = list(range(10)) random.shuffle(li) obj = bubble_sort(li) print(obj)
# 选择排序 - 一趟遍历记录最小的数,放到第一个位置;再一趟遍历记录剩余列表中最小的数,继续放置... - 时间复杂度 O(n^2) def select_sort(li): for i in range(len(li) - 1): #i 趟 min_loc = i # 找i+1位置到最后面位置内最小的数 for j in range(i+1,len(li)): if li[j] < li[min_loc]: min_loc = j # 和无序区第一个数作交换 li[min_loc],li[i] = li[i],li[min_loc] return li obj = select_sort([1,8,6,2,5,3]) print(obj)
#插入排序 - 列表被分为有序区和无序区 最初有序区只有一个元素 - 每次从无序区选择一个元素 插入到有序区的位置 直到无序区变空 #方式一: def insert_sort(li): for i in range(1,len(li)): # i 代表每次摸到牌的下标 tmp = li[i] j = i-1 # j代表手里最后一张牌的下标 while True: if j<0 or tmp>=li[j]: break li[j+1] = li[j] j -= 1 li[j+1] = tmp return li obj = insert_sort([1,8,6,2,5,3]) print(obj) #方式二: def insert_sort(li): for i in range(1,len(li)): # i 代表每次摸到牌的下标 tmp = li[i] j = i-1 # j代表手里最后一张牌的下标 while j>=0 and tmp<li[j]: li[j+1] = li[j] j -= 1 li[j+1] = tmp return li obj = insert_sort([1,8,6,2,5,3]) print(obj)
def partition(data,left,right): tmp = data[left] while left < right: # right 左移动 while left < right and data[right] >= tmp: #如果low和high没有相遇且后面的数一直大于第一个数 就循环 right -=1 data[left] = data[right] # left 右移动 while left < right and data[left] <= tmp: #如果low和high没有相遇且后面的数一直大于第一个数 就循环 left +=1 data[right] = data[left] data[left] = tmp return left def quick_sork(data,left,right): if left <right: mid = partition(data,left,right) quick_sork(data,left,mid-1) quick_sork(data,mid+1,right) return data alist = [33,22,11,55,33,666,55,44,33,22,980] obj = quick_sork(alist,0,len(alist)-1) print(obj)
