无所不能的Embedding1 - 词向量三巨头之Word2vec模型详解&代码实现
word2vec是google 2013年提出的,从大规模语料中训练词向量的模型,在许多场景中都有应用,信息提取相似度计算等等。也是从word2vec开始,embedding在各个领域的应用开始流行,所以拿word2vec来作为开篇再合适不过了。本文希望可以较全面的给出Word2vec从模型结构概述,推导,训练,和基于tf.estimator实现的具体细节。完整代码戳这里 https://github.com/DSXiangLi/Embedding
模型概述
word2vec模型结构比较简单,是为了能够在大规模数据上训练,降低了模型复杂度,移除了非线性隐藏层。根据不同的输入输出形式又分成CBOW和SG两种方法。
让我们先把问题简化成1v1的bigram问题,单词i作为context,单词j是target。V是单词总数,N是词向量长度,D是训练词对,输入\(x_i \in R ^{1*V}\)是one-hot向量。

模型训练两个权重矩阵,\(W \in R ^{V*N}\)是输入矩阵,每一行对应输入单词的词向量,\(W^{'} \in R ^{V*N}\)是输出矩阵,每一行对应输出单词的词向量。词i和词j的共现信息用词向量的内积来表达,通过softmax得到每个单词的概率如下
对每个训练样本,模型的目标是最大化条件概率\(p(w_j|w_I)\), 因此我们的对数损失函数如下
CBOW : Continuous bag of words
CBOW是把bigram的输入context,扩展成了目标单词周围2*window_size内的单词,用中心词前后的语境来预测中心词。
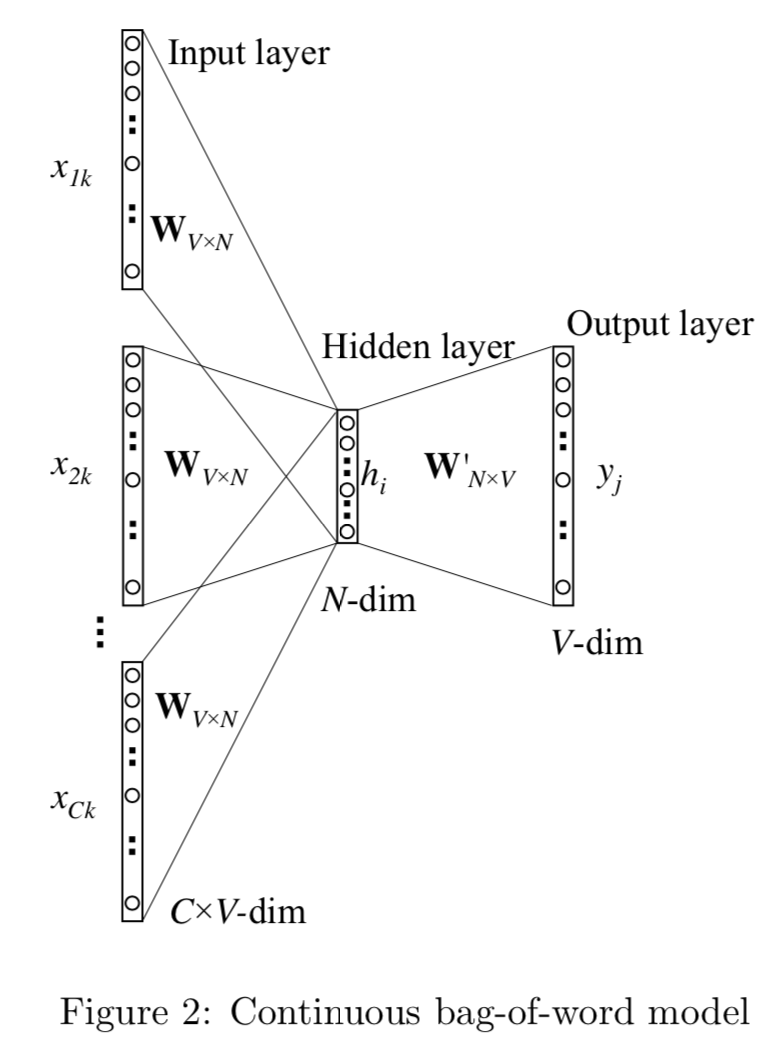
对比bigram, CBOW只多做了一步操作,对输入的2 * Window_size个单词,在映射得到词向量后,需要做average_pooling得到1*N的输入向量, 所以差异只在h的计算。假定$C = 2 * \text{window_size}$ $$ \begin{align} h & = \frac{1}{C}W^T(x_1 + x_2 +... + x_C) \\ & = \frac{1}{C}(v_{w1} + v_{w2} + ... + v_{wc}) ^T \\ E &= -log \, p(w_O|w_{I,1}...w_{I,C}) \\ & = -u_j^* + log\sum_{j^{'}=1}^Vexp(u_{j^{'}}) \end{align} $$
SG : Skip Gram
SG是把bigram的输出target,扩展成了输入单词周围2*window_size内的单词,用中心词来预测周围单词的出现概率。
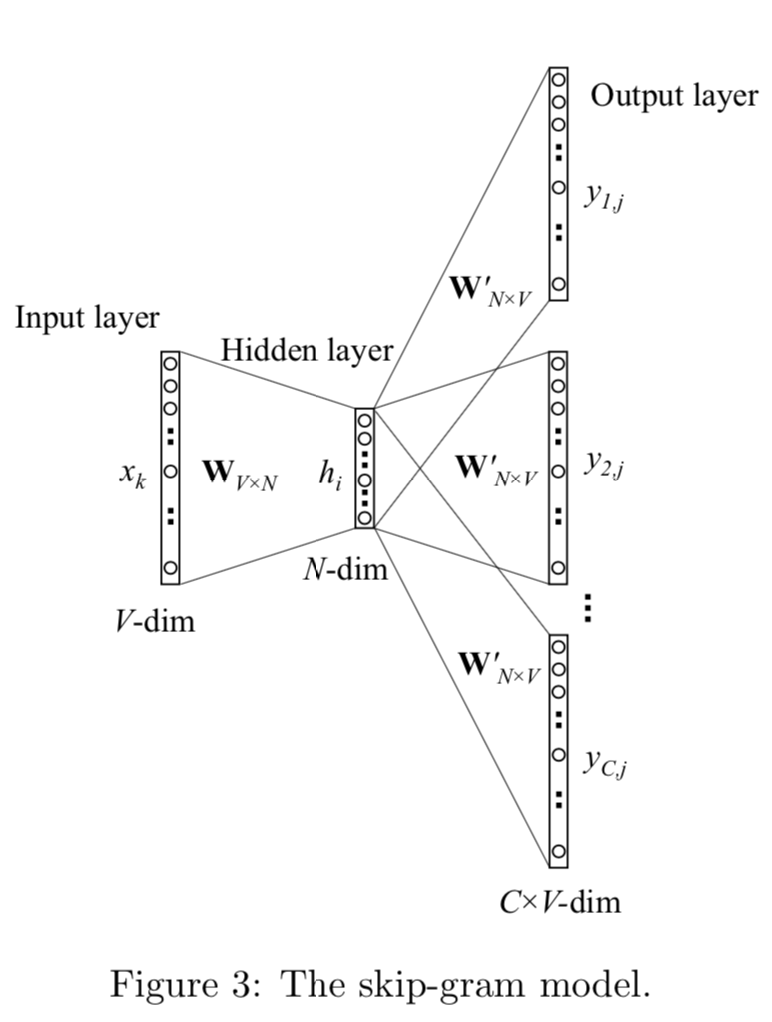
对比bigram,SG的差异只在于输出概率多项分布不再是一个而是C个
模型推导:word embedding是如何得到的?
下面我们从back propogation推导下以上模型结构是如何学到词向量的,为简化我们还是先从bigram来看,\(\eta\)是learning rate。
首先是hidden->output \(W^{'}\)的词向量的更新
\(e_j\)是单词j的预测概率误差,所以\(W^{'}\)的更新可以理解为如果单词j被高估就从\(v_{w^{'}j}\)中减去\(\eta \cdot e_j \cdot h\),降低h和\(v_{w^{'}j}\)的向量内积(similarity),反之被低估则在\(v_{w^{'}j}\)上叠加\(\eta \cdot e_j \cdot h\)增加内积相似度,误差越大更新的幅度越大。
然后是input->hidden W的词向量的更新
每个输入单词对应的词向量\(v_{wI}\),都用所有单词的输出词向量按预测误差加权平均得到的向量进行更新。和上述的逻辑相同高估做subtraction,低估的做addition然后按误差大小进行加权来更新输入词向量。
所以模型学习过程会是输入词向量更新输出词向量,输出词向量再更新输入词向量,然后back-and-forth到达稳态。
把bigram拓展到CBOW,唯一的变化在于更新input-hidden的词向量时,不是每次更新一个单词对应的向量,而是用相同的幅度同时更新C个单词的词向量.
把bigram拓展到SG,唯一的变化在于更新hidden-output的词向量时,不再是用单词j的预测误差,而是用C个单词的预测误差之和
模型训练
虽然模型结构已经做了优化,移除了非线性的隐藏层,但是模型训练起来并不高效,瓶颈在于Word2vec本质是多分类任务,类别有整个vocabulary这么多,所以\(p(w_j|w_I) = \frac{exp(u_j)}{\sum_{j^{'}=1}^Vexp(u_{j^{'}})}\)每次需要计算整个vocabulary的概率\(O(VN)\)。即便batch只有1个训练样本,也需要更新所有单词hidden->output的embedding矩阵。针对这个问题有两种解决方案
Hierarchical Softmax
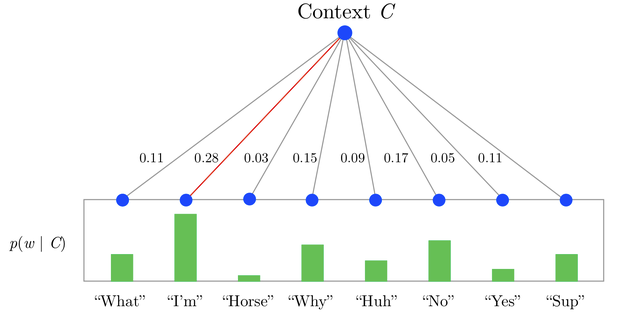
如果把softmax看作一个1-layer tree,每个单词都是一个叶节点, 因为需要归一化所以计算每个单词的概率的复杂度是\(O(V)\)。Hierarchical Softmax只是把1-layer变成了multi-layer,在不增加embedding大小的情况下(V个叶节点,树有V-1个inner node), 把计算每个单词概率的复杂度降低到\(O(logV)\),直接用从root到叶节点的路径来计算每个单词的概率。树的构造作者选用了huffman tree,优点在于高频词从root到leaf的路径会比低频词更短,这样可以进一步加速训练,具体细节可以来看这篇博客huffman coding
例如下图(图片来源)
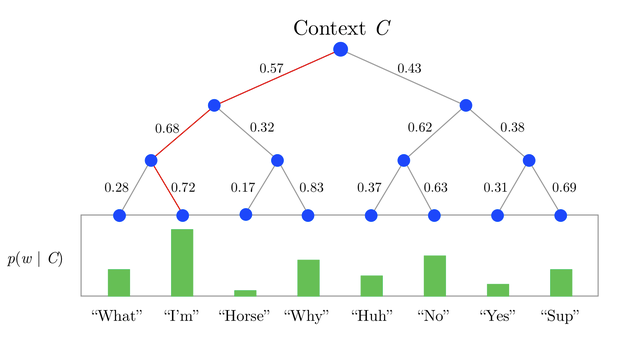
$$ \begin{align} P(Horse) &= P(0,left)\cdot P(1,right)\cdot P(2,left) \end{align} $$
那具体上面的p(0,left)要如何计算呢?
每一个node都有自己的embedding \(v_n{(w,j)}\), 既单词w路径上第j个node的embedding,输入输出的单词内积,变为输入单词和node的内积, 每个单词的概率计算如下
不得不说这个式子写的真是生怕别人能看懂>_<
\([n(w,j+1) = ch(n(w,j))]\) 是个啥?ch是left child,\([\cdot]\)只是用来判断path是往左还是往右
所以
对应上面的模型推导,hidden->ouput的部分发生变化, 损失函数变为以下
每次output单词对应的路径上的embedding会被更新,预测任务变为该路径上每个inner_node应该往左还是往右。
简单的huffman Hierarchy softmax的实现如下
class TreeNode(object):
total_node = 0
def __init__(self, frequency, char = None , word_index = None, is_leaf = False):
self.frequency = frequency
self.char = char # word character
self.word_index = word_index # word look up index
self.left = None
self.right = None
self.is_leaf = is_leaf
self.counter(is_leaf)
def counter(self, is_leaf):
# node_index will be used for embeeding_lookup
self.node_index = TreeNode.total_node
if not is_leaf: TreeNode.total_node += 1
def __lt__(self, other):
return self.frequency < other.frequency
def __repr__(self):
if self.is_leaf:
return 'Leaf Node char = [{}] index = {} freq = {}'.format(self.char, self.word_index, self.frequency)
else:
return 'Inner Node [{}] freq = {}'.format(self.node_index, self.frequency)
class HuffmanTree(object):
def __init__(self, freq_dic):
self.nodes = []
self.root = None
self.max_depth = None
self.freq_dic = freq_dic
self.all_paths = {}
self.all_codes = {}
self.node_index = 0
@staticmethod
def merge_node(left, right):
parent = TreeNode(left.frequency + right.frequency)
parent.left = left
parent.right = right
return parent
def build_tree(self):
"""
Build huffman tree with word being leaves
"""
TreeNode.total_node = 0 # avoid train_and_evaluate has different node_index
heap_nodes = []
for word_index, (char, freq) in enumerate(self.freq_dic.items()):
tmp = TreeNode( freq, char, word_index, is_leaf=True )
heapq.heappush(heap_nodes, tmp )
while len(heap_nodes)>1:
node1 = heapq.heappop(heap_nodes)
node2 = heapq.heappop(heap_nodes)
heapq.heappush(heap_nodes, HuffmanTree.merge_node(node1, node2))
self.root = heapq.heappop(heap_nodes)
@property
def num_node(self):
return self.root.node_index + 1
def traverse(self):
"""
Compute all node to leaf path and direction: list of node_id, list of 0/1
"""
def dfs_helper(root, path, code):
if root.is_leaf :
self.all_paths[root.word_index] = path
self.all_codes[root.word_index] = code
return
if root.left :
dfs_helper(root.left, path + [root.node_index], code + [0])
if root.right :
dfs_helper(root.right, path + [root.node_index], code + [1])
dfs_helper(self.root, [], [] )
self.max_depth = max([len(i) for i in self.all_codes.values()])
class HierarchySoftmax(HuffmanTree):
def __init__(self, freq_dic):
super(HierarchySoftmax, self).__init__(freq_dic)
def convert2tensor(self):
# padded to max_depth and convert to tensor
with tf.name_scope('hstree_code'):
self.code_table = tf.convert_to_tensor([ code + [INVALID_INDEX] * (self.max_depth - len(code)) for word, code
in sorted( self.all_codes.items(), key=lambda x: x[0] )],
dtype = tf.float32)
with tf.name_scope('hstree_path'):
self.path_table = tf.convert_to_tensor([path + [INVALID_INDEX] * (self.max_depth - len(path)) for word, path
in sorted( self.all_paths.items(), key=lambda x: x[0] )],
dtype = tf.int32)
def get_loss(self, input_embedding_vector, labels, output_embedding, output_bias, params):
"""
:param input_embedding_vector: [batch * emb_size]
:param labels: word index [batch * 1]
:param output_embedding: entire embedding matrix []
:return:
loss
"""
loss = []
labels = tf.unstack(labels, num = params['batch_size']) # list of [1]
inputs = tf.unstack(input_embedding_vector, num = params['batch_size']) # list of [emb_size]
for label, input in zip(labels, inputs):
path = self.path_table[tf.squeeze(label)]# (max_depth,)
code = self.code_table[tf.squeeze(label)] # (max_depth,)
path = tf.boolean_mask(path, tf.not_equal(path, INVALID_INDEX)) # (real_path_length,)
code = tf.boolean_mask(code, tf.not_equal(code, INVALID_INDEX) ) # (real_path_length,)
output_embedding_vector = tf.nn.embedding_lookup(output_embedding, path) # real_path_length * emb_size
bias = tf.nn.embedding_lookup(output_bias, path) # (real_path_length,)
logits = tf.matmul(tf.expand_dims(input, axis=0), tf.transpose(output_embedding_vector) ) + bias # (1,emb_size) *(emb_size, real_path_length)
loss.append(tf.nn.sigmoid_cross_entropy_with_logits(labels = code, logits = tf.squeeze(logits) ))
loss = tf.reduce_mean(tf.concat(loss, axis = 0), axis=0, name = 'hierarchy_softmax_loss') # batch -> scaler
return loss
Negative Sampling
Negative Sampling理解起来更加直观,因为模型的目标是训练出高质量的word embedding,也就是input word embedding,那是否每个batch都更新全部的output word embedding并不重要,我们可以每次只sample K个embedding来做更新。原始的正样本保留,我们再采样 K组负样本来进行训练,模型只需要学习正样本vs负样本,也就绕过了用V个单词来做归一化的问题,把多分类问题成功简化为二分类问题。作者表示小样本K=520,大样本k=25。
对应上述的模型推导,hidden->output的部分发生变化, 损失函数变为
每个iteration只有K个embedding被更新
而input->hidden的部分,只有k个embedding的加权向量会用于输入embedding的更新
tensorflow有几种candidate sample的实现,两种比较常用的是nn.sampled_softmax_loss和nn.nce_loss, 它们调用了相同的采样函数。差异在于sampled_softmax_loss用的是softmax(排他单分类),而nce_loss是求logistic (不排他多分类)。这两种实现都和negative sampling有些许差异,细节可以看下Notes on Noise Contrastive Estimation and Negative Sampling。而这二者之间比较是有观点说nce更适合skip-gram, sample更适合CBOW,具体差异我也还得再多用用试试看。
Subsampling
论文还有一个重点是subsampling,针对出现频率高的词,对于它们过多的训练样本不能进一步提高表现,因此可以对这些样本进行downsample。t是词频阈值, \(f(w_i)\)是单词在corpus里的出现频率,所有出现频率高于t的单词,都会按照以下概率被降采样
模型实现
手残党现实体验是word2vec比较复杂的部分不是模型。。。而是input_pipe和loss function,所以在实现的时候也希望尽可能把dataset, model_fn, 和train的部分分割开来。以下只给出model_fn的核心部分
def avg_pooling_embedding(embedding, features, params):
"""
:param features: (batch, 2*window_size)
:param embedding: (vocab_size, emb_size)
:return:
input_embedding : average pooling of context embedding
"""
input_embedding= []
samples = tf.unstack(features, params['batch_size'])
for sample in samples:
sample = tf.boolean_mask(sample, tf.not_equal(sample, INVALID_INDEX), axis=0) # (real_size,)
tmp = tf.nn.embedding_lookup(embedding, sample) # (real_size, emb_size)
input_embedding.append(tf.reduce_mean(tmp, axis=0)) # (emb_size, )
input_embedding = tf.stack(input_embedding, name = 'input_embedding_vector') # batch * emb_size
return input_embedding
def model_fn(features, labels, mode, params):
if params['train_algo'] == 'HS':
# If Hierarchy Softmax is used, initialize a huffman tree first
hstree = HierarchySoftmax( params['freq_dict'] )
hstree.build_tree()
hstree.traverse()
hstree.convert2tensor()
if params['model'] == 'CBOW':
features = tf.reshape(features, shape = [-1, 2 * params['window_size']])
labels = tf.reshape(labels, shape = [-1,1])
else:
features = tf.reshape(features, shape = [-1,])
labels = tf.reshape(labels, shape = [-1,1])
with tf.variable_scope( 'initialization' ):
w0 = tf.get_variable( shape=[params['vocab_size'], params['emb_size']],
initializer=tf.truncated_normal_initializer(), name='input_word_embedding' )
if params['train_algo'] == 'HS':
w1 = tf.get_variable( shape=[hstree.num_node, params['emb_size']],
initializer=tf.truncated_normal_initializer(), name='hierarchy_node_embedding' )
b1 = tf.get_variable( shape = [hstree.num_node],
initializer=tf.random_uniform_initializer(), name = 'bias')
else:
w1 = tf.get_variable( shape=[params['vocab_size'], params['emb_size']],
initializer=tf.truncated_normal_initializer(), name='output_word_embedding' )
b1 = tf.get_variable( shape=[params['vocab_size']],
initializer=tf.random_uniform_initializer(), name='bias')
add_layer_summary( w0.name, w0)
add_layer_summary( w1.name, w1 )
add_layer_summary( b1.name, b1 )
with tf.variable_scope('input_hidden'):
# batch_size * emb_size
if params['model'] == 'CBOW':
input_embedding_vector = avg_pooling_embedding(w0, features, params)
else:
input_embedding_vector = tf.nn.embedding_lookup(w0, features, name = 'input_embedding_vector')
add_layer_summary(input_embedding_vector.name, input_embedding_vector)
with tf.variable_scope('hidden_output'):
if params['train_algo'] == 'HS':
loss = hstree.get_loss( input_embedding_vector, labels, w1, b1, params)
else:
loss = negative_sampling(mode = mode,
output_embedding = w1,
bias = b1,
labels = labels,
input_embedding_vector =input_embedding_vector,
params = params)
optimizer = tf.train.AdagradOptimizer( learning_rate = params['learning_rate'] )
update_ops = tf.get_collection( tf.GraphKeys.UPDATE_OPS )
with tf.control_dependencies( update_ops ):
train_op = optimizer.minimize( loss, global_step= tf.train.get_global_step() )
return tf.estimator.EstimatorSpec( mode, loss=loss, train_op=train_op )
留言,评论,吐槽代码的都欢迎哈~
Ref
- [Word2Vec A]Tomas Mikolov et al, 2013, Efficient Edtimation of Word Representations in Vector Space
- [Word2Vec B]Tomas Mikolow et al, 2013, Distributed Representations of Words and Phrases and their Compositionality
- Yoav GoldBerg, Omer Levy, 2014, Wor2Vec Explained: Deribing Mikolow et al's Negative-Sampling Word Embedding Method
- Xin Rong, 2016, word2vec ParameterLearning Explained
- [Candidate Sampling]https://www.tensorflow.org/extras/candidate_sampling.pdf
- [Negative Sampling]Chris Dyer, 2014, Notes on Noise Contrastive Estimation and Negative Sampling
- https://github.com/chao-ji/tf-word2vec
- https://github.com/akb89/word2vec
- https://ruder.io/word-embeddings-softmax/index.html#negativesampling
- https://blog.csdn.net/lilong117194/article/details/82849054



