CTR学习笔记&代码实现6-深度ctr模型 后浪 xDeepFM/FiBiNET
xDeepFM用改良的DCN替代了DeepFM的FM部分来学习组合特征信息，而FiBiNET则是应用SENET加入了特征权重比NFM，AFM更进了一步。在看两个model前建议对DeepFM, Deep&Cross, AFM，NFM都有简单了解，不熟悉的可以看下文章最后其他model的博客链接。
以下代码针对Dense输入更容易理解模型结构，针对spare输入的代码和完整代码 👇
https://github.com/DSXiangLi/CTR
xDeepFM
模型结构
看xDeepFM的名字和DeepFM相似都拥有Deep和Linear的部分，只不过把DeepFM中用来学习二阶特征交互的FM部分替换成了CIN（Compressed Interactino Network）。而CIN是在Deep&Cross的DCN上进一步改良的得到。整体模型结构如下
我们重点看下CIN的部分，和paper的notation保持一致，有m个特征，每个特征Embedding是D维，第K层的CIN有\(H_k\)个unit。CIN第K层的计算分为3个部分分别对应图a-c：
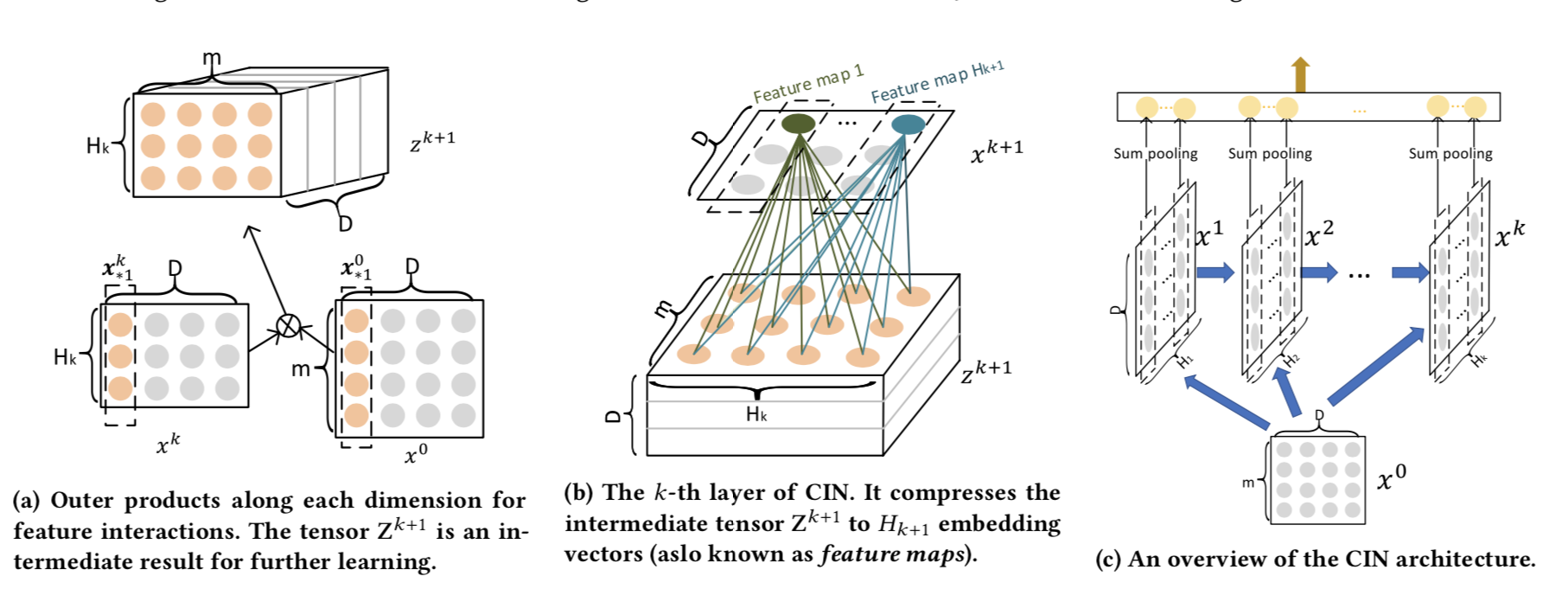
- 向量两两做element-wise product, 时间复杂度\(O(m*H_{k-1}*D)\)
对输入层和第K-1层输出，做element-wise乘积进行两两特征交互，得到\(m*H_{k-1}\)个D维向量矩阵，如果CIN只有一层，则和FM, NFM，AFM的第一步相同。FM 直接聚合成scaler，NFM沿D进行sum_pooling，而AFM加入Attention沿D进行weighted_pooling。忽略batch的矩阵dimension变化如下
\[z^k = x^0 \odot x^{k-1} = (D * m* 1) \odot (D * 1* H_{k-1}) = D * m*H_{k-1}
\]
- Feature Map，空间复杂度\(O(H_k *H_{k-1} *m)\)，时间复杂度\(O(H_k *H_{k-1} *m*D)\)
\(W_k \in R^{H_{k-1}*m *H_k}\) 是第K层的权重向量，可以理解为沿Embedding做CNN。每个Filter对所有两两乘积的向量进行加权求和得到 \(1*D\)的向量 一共有\(H_k\)个channel，输出\(H_k * D\)的矩阵向量。
\[w^k \bullet z^k = (H_k *H_{k-1} *m)* (m*H_{k-1}*D) = H_k *D
\]
- Sum Pooling
CIN对每层的输出沿Dimension进行sum pooling，得到\(H_k*1\)的输出，然后把每层输出concat以后作为CIN部分的输出。
CIN每一层的计算如上，T层CIN每一层都是上一次层的输出和第一层的输入进行交互得到更高一阶的交互信息。假设每层维度一样\(H_k=H\)， CIN 部分整体时间复杂度是\(O(TDmH^2)\)，空间复杂度来自每层的Filter权重\(O(TmH^2)\)
CIN保留DCN的任意高阶和参数共享，两个主要差别是
- DCN是bit-wise，CIN是vector-wise。DCN在做向量乘积时不区分Field，直接对所有Field拼接成的输入（m*D）进行外积。而CIN考虑Field，两两vector进行乘积
- DCN使用了ResNet因为多项式的核心只用输出最后一层，而CIN则是每层都进行pooling后输出
CIN的设计还是很巧妙滴，不过。。。吐槽小分队上线: CIN不论是时间复杂度还是空间复杂度都比DCN要高，感觉更容易过拟合。至于说vector-wise的向量乘积要比bit-wise的向量乘积要好，这。。。至少bit-wise可以不限制embedding维度一致, 但vector-wise嘛我实在有些理解无能，明白的童鞋可以comment一下
代码实现
def cross_op(xk, x0, layer_size_prev, layer_size_curr, layer, emb_size, field_size):
# Hamard product: ( batch * D * HK-1 * 1) * (batch * D * 1* H0) -> batch * D * HK-1 * H0
zk = tf.matmul( tf.expand_dims(tf.transpose(xk, perm = (0, 2, 1)), 3),
tf.expand_dims(tf.transpose(x0, perm = (0, 2, 1)), 2))
zk = tf.reshape(zk, [-1, emb_size, field_size * layer_size_prev]) # batch * D * HK-1 * H0 -> batch * D * (HK-1 * H0)
add_layer_summary('zk_{}'.format(layer), zk)
# Convolution with channel = HK: (batch * D * (HK-1*H0)) * ((HK-1*H0) * HK)-> batch * D * HK
kernel = tf.get_variable(name = 'kernel{}'.format(layer),
shape = (field_size * layer_size_prev, layer_size_curr))
xkk = tf.matmul(zk, kernel)
xkk = tf.transpose(xkk, perm = [0,2,1]) # batch * HK * D
add_layer_summary( 'Xk_{}'.format(layer), xkk )
return xkk
def cin_layer(x0, cin_layer_size, emb_size, field_size):
cin_output_list = []
cin_layer_size.insert(0, field_size) # insert field dimension for input
with tf.variable_scope('Cin_component'):
xk = x0
for layer in range(1, len(cin_layer_size)):
with tf.variable_scope('Cin_layer{}'.format(layer)):
# Do cross
xk = cross_op(xk, x0, cin_layer_size[layer-1], cin_layer_size[layer],
layer, emb_size, field_size ) # batch * HK * D
# sum pooling on dimension axis
cin_output_list.append(tf.reduce_sum(xk, 2)) # batch * HK
return tf.concat(cin_output_list, axis=1)
@tf_estimator_model
def model_fn_dense(features, labels, mode, params):
dense_feature, sparse_feature = build_features()
dense_input = tf.feature_column.input_layer(features, dense_feature)
sparse_input = tf.feature_column.input_layer(features, sparse_feature)
# Linear part
with tf.variable_scope('Linear_component'):
linear_output = tf.layers.dense( sparse_input, units=1 )
add_layer_summary( 'linear_output', linear_output )
# Deep part
dense_output = stack_dense_layer( dense_input, params['hidden_units'],
params['dropout_rate'], params['batch_norm'],
mode, add_summary=True )
# CIN part
emb_size = dense_feature[0].variable_shape.as_list()[-1]
field_size = len(dense_feature)
embedding_matrix = tf.reshape(dense_input, [-1, field_size, emb_size]) # batch * field_size * emb_size
add_layer_summary('embedding_matrix', embedding_matrix)
cin_output = cin_layer(embedding_matrix, params['cin_layer_size'], emb_size, field_size)
with tf.variable_scope('output'):
y = tf.concat([dense_output, cin_output,linear_output], axis=1)
y = tf.layers.dense(y, units= 1)
add_layer_summary( 'output', y )
return y
FiBiNET
模型结构
看FiBiNET前可以先了解下Squeeze-and-Excitation Network,感兴趣可以看下这篇博客Squeeze-and-Excitation Networks。
FiBiNET的主要创新是应用SENET学习每个特征的重要性，加权得到新的Embedding矩阵。在FiBiNET之前，AFM，PNN，DCN和上面的xDeepFM都是在特征交互之后才用attention, 加权等方式学习特征交互的权重，而FiBiNET在保留这部分的同时，在Embedding部分就考虑特征自身的权重。模型结构如下
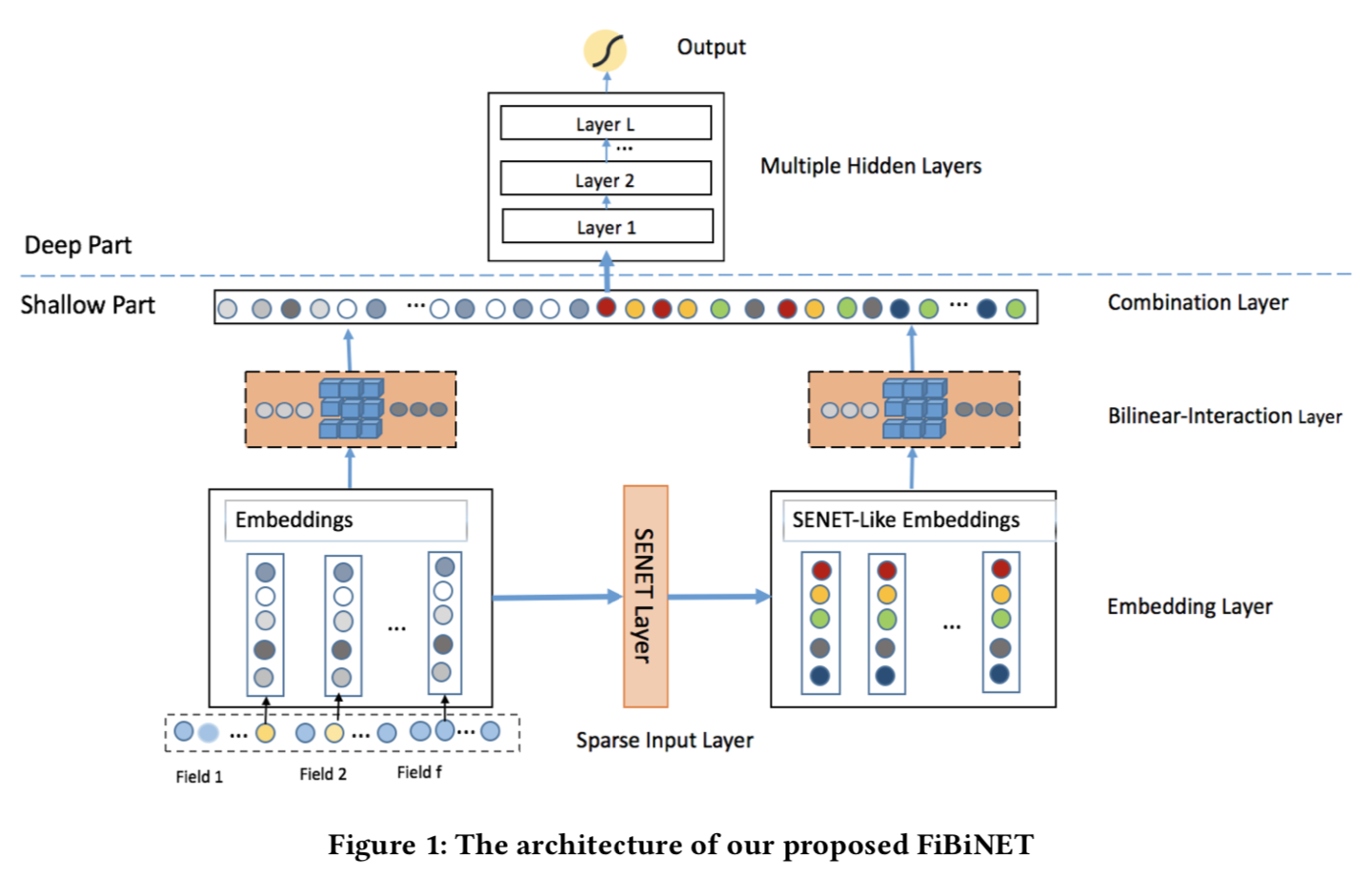
原始Embedding，和经过SENET调整过权重的新Embedding，在Bilinear-interaction层学习二阶交互特征，拼接后，再经过MLP进一步学习高阶特征。和paper notation保持一致（啊啊啊大家能不能统一下notation搞的我自己看自己的注释都蒙圈），f个特征，k维embedding
SENET层
SENET层学习每个特征的权重对Embedding进行加权，分为以下3步
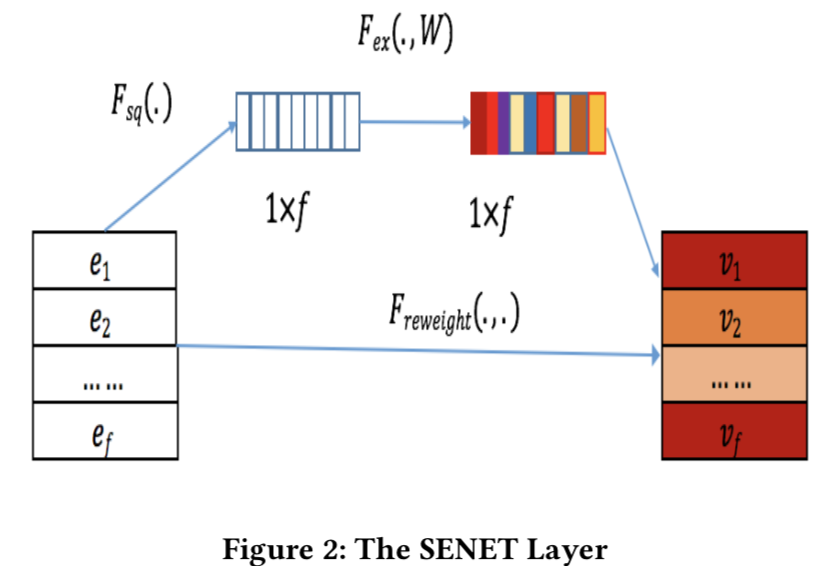
- Squeeze
把\(f*k\)的Embedding矩阵压缩成\(f*1\), 压缩方式不固定，SENET原paper用的max_pooling,作者用的sum_pooling，感觉这里压缩方式应该取决于Embedding的信息表达
\[\begin{align}
E &= [e_1,...,e_f] \\
Z &= [z_1,...,z_f] \\
z_i &= F_{squeeze}(e_i) = \frac{1}{k}\sum_{i=1}^K e_i \\
\end{align}
\]
- Excitation
Excitation是一个两层的全连接层，通过先降维再升维的方式过滤一些无用特征，降维的幅度通过额外变量\(r\)来控制，第一层权重\(W_1 \in R^{f*f/r}\),第二层权重\(W_2 \in R^{f/r*f}\)。这里r越高，压缩的幅度越高，最终的权重会更集中,反之会更分散。
\[A = \sigma_2(W_2·\sigma_1(W_1·Z))
\]
- Re-weight
最后一步就是用Excitation得到的每个特征的权重对Embedding进行加权得到新Embedding
\[E_{new} = F_{Reweight}(A,E) = [a_1·e_1, ...,a_f·e_f ]
\]
在收入数据集上进行尝试，r=2时会有46%的embedding特征权重为0，所以SENET会在特征交互前先过滤部分对target无用的特征来增加有效特征的权重
Bilinear-Interaction层
作者提出内积和element-wise乘积都不足以捕捉特征交互信息，因此进一步引入权重W，以下面的方式进行特征交互
\[v_i · W \odot v_j
\]
其中W有三种选择，可以所有特征交互共享一个权重矩阵(Field-All),或者每个特征和其他特征的交互共享权重(Field-Each), 再或者每个特征交互一个权重(Field-Interaction) 具体的优劣感觉需要casebycase来试，不过一般还是照着数据越少参数越少的逻辑来整。
原始Embedding和调整权重后的Embedding在Bilinear-Interaction学习交互特征后，拼接成shallow 层，再经过全连接层来学习更高阶的特征交互。后面的属于常规操作这里就不再细说。
我们不去吐槽FiBiNET可以加入wide&deep框架来捕捉低阶特征信息和任意高阶信息，更多把FiBiNET提供的SENET特征权重的思路放到自己的工具箱中就好。
代码实现
def Bilinear_layer(embedding_matrix, field_size, emb_size, type, name):
# Bilinear_layer: combine inner and element-wise product
interaction_list = []
with tf.variable_scope('BI_interaction_{}'.format(name)):
if type == 'field_all':
weight = tf.get_variable( shape=(emb_size, emb_size), initializer=tf.truncated_normal_initializer(),
name='Bilinear_weight_{}'.format(name) )
for i in range(field_size):
if type == 'field_each':
weight = tf.get_variable( shape=(emb_size, emb_size), initializer=tf.truncated_normal_initializer(),
name='Bilinear_weight_{}_{}'.format(i, name) )
for j in range(i+1, field_size):
if type == 'field_interaction':
weight = tf.get_variable( shape=(emb_size, emb_size), initializer=tf.truncated_normal_initializer(),
name='Bilinear_weight_{}_{}_{}'.format(i,j, name) )
vi = tf.gather(embedding_matrix, indices = i, axis =1, batch_dims =0, name ='v{}'.format(i)) # batch * emb_size
vj = tf.gather(embedding_matrix, indices = j, axis =1, batch_dims =0, name ='v{}'.format(j)) # batch * emb_size
pij = tf.matmul(tf.multiply(vi,vj), weight) # bilinear : vi * wij \odot vj
interaction_list.append(pij)
combination = tf.stack(interaction_list, axis =1 ) # batch * emb_size * (Field_size * (Field_size-1)/2)
combination = tf.reshape(combination, shape = [-1, int(emb_size * (field_size * (field_size-1) /2)) ]) # batch * ~
add_layer_summary( 'bilinear_output', combination )
return combination
def SENET_layer(embedding_matrix, field_size, emb_size, pool_op, ratio):
with tf.variable_scope('SENET_layer'):
# squeeze embedding to scaler for each field
with tf.variable_scope('pooling'):
if pool_op == 'max':
z = tf.reduce_max(embedding_matrix, axis=2) # batch * field_size * emb_size -> batch * field_size
else:
z = tf.reduce_mean(embedding_matrix, axis=2)
add_layer_summary('pooling scaler', z)
# excitation learn the weight of each field from above scaler
with tf.variable_scope('excitation'):
z1 = tf.layers.dense(z, units = field_size//ratio, activation = 'relu')
a = tf.layers.dense(z1, units= field_size, activation = 'relu') # batch * field_size
add_layer_summary('exciitation weight', a )
# re-weight embedding with weight
with tf.variable_scope('reweight'):
senet_embedding = tf.multiply(embedding_matrix, tf.expand_dims(a, axis = -1)) # (batch * field * emb) * ( batch * field * 1)
add_layer_summary('senet_embedding', senet_embedding) # batch * field_size * emb_size
return senet_embedding
@tf_estimator_model
def model_fn_dense(features, labels, mode, params):
dense_feature, sparse_feature = build_features()
dense_input = tf.feature_column.input_layer(features, dense_feature)
sparse_input = tf.feature_column.input_layer(features, sparse_feature)
# Linear part
with tf.variable_scope('Linear_component'):
linear_output = tf.layers.dense( sparse_input, units=1 )
add_layer_summary( 'linear_output', linear_output )
field_size = len(dense_feature)
emb_size = dense_feature[0].variable_shape.as_list()[-1]
embedding_matrix = tf.reshape(dense_input, [-1, field_size, emb_size])
# SENET_layer to get new embedding matrix
senet_embedding_matrix = SENET_layer(embedding_matrix, field_size, emb_size,
pool_op = params['pool_op'], ratio= params['senet_ratio'])
# combination layer & BI_interaction
BI_org = Bilinear_layer(embedding_matrix, field_size, emb_size, type = params['bilinear_type'], name = 'org')
BI_senet = Bilinear_layer(senet_embedding_matrix, field_size, emb_size, type = params['bilinear_type'], name = 'senet')
combination_layer = tf.concat([BI_org, BI_senet] , axis =1)
# Deep part
dense_output = stack_dense_layer(combination_layer, params['hidden_units'],
params['dropout_rate'], params['batch_norm'],
mode, add_summary=True )
with tf.variable_scope('output'):
y = dense_output + linear_output
add_layer_summary( 'output', y )
return y
CTR学习笔记&代码实现系列👇
https://github.com/DSXiangLi/CTR
CTR学习笔记&代码实现1-深度学习的前奏 LR->FFM
CTR学习笔记&代码实现2-深度ctr模型 MLP->Wide&Deep
CTR学习笔记&代码实现3-深度ctr模型 FNN->PNN->DeepFM
CTR学习笔记&代码实现4-深度ctr模型 NFM/AFM
CTR学习笔记&代码实现5-深度ctr模型 DeepCrossing -> Deep&Cross
Ref
- Jianxun Lian, 2018, xDeepFM: Combining Explicit and Implicit Feature Interactions for Recommender Systems
- Tongwen Huang, 2019, FiBiNET: Combining Feature Importance and Bilinear feature Interaction for Click-Through Rate Prediction
- Jie Hu, 2017, Squeeze-and-Excitation Networks
- https://zhuanlan.zhihu.com/p/72931811
- https://zhuanlan.zhihu.com/p/79659557
- https://zhuanlan.zhihu.com/p/57162373
- https://github.com/qiaoguan/deep-ctr-prediction
