AB实验人群定向HTE模型5 - Meta Learner

Meta Learner和之前介绍的Causal Tree直接估计模型不同，属于间接估计模型的一种。它并不直接对treatment effect进行建模，而是通过对response effect(target)进行建模，用treatment带来的target变化作为HTE的估计。主要方法有3种:T-Learner, S-Learner, X-Learner，思路相对比较传统的是在监督模型的基础上去近似因果关系。

Meta-Learner的优点很明显，可以使用任意ML监督模型进行拟合不需要构建新的estimator。所以如果有必需要基于DNN/LGB的需求不妨用Meta-Learner作为Benchamrk

核心论文

Künzel, S. R., Sekhon, J. S., Bickel, P. J., & Yu, B. (2019). Metalearners for estimating heterogeneous treatment effects using machine learning. Proceedings of the National Academy of Sciences, 116(10), 4156–4165.

模型

T-Learner

T是two的缩写，是比较传统的ML模型用于因果推理的方式。对照组和实验组进行分别建模得到两个模型,对每个样本计算两个模型的预测值之差作为HTE的估计

\[\begin{align} \mu_0(x) = E[Y (0)|X = x]\\ \mu_1(x) = E[Y (1)|X = x]\\ \hat{\tau}(x) = \hat{\mu}_1 (x) - \hat{\mu}_0(x) \end{align} \]

T-Learner有3个很明显的问题

1. 对照组的模型无法学到实验组的pattern，实验组的模型也无法用到对照组的数据。两个模型完全隔离，也就导致两个模型可能各自有各自的偏差，从而导致的预测产生较大的误差。
2. T-Learner限制了Treatment只能是离散值
3. 大多数情况下treatment effect和response相比都是很小的，因此在response上的估计偏差会对treatment有很大影响

S-Learner

S是Single的缩写，把对照组和实验组放在一起建模，把实验分组作为特征加入训练特征。然后用Imputation的方法计算如果该样本进入实验组vs对照组模型预测的差异作为对实验影响的估计。

\[\begin{align} μ(x, w) &= E[Y|X = x, W = w]\\ \hat{\tau}(x) &= \hat{\mu} (x,1) - \hat{\mu}(x,0) \end{align} \]

S-Learner的问题同样在于本质是对response进行拟合。如果使用树作为Base-learner,最终的HTE可以简单理解为样本落在不同的叶节点，叶节点的样本差异。但因为树本身是对outcome进行建模而非对treatment effect进行建模，很有可能有效的人群划分方式在这种情况下并学习不到。

S-Learner的思想很常见，和可解释机器学习中的Individual Conditional Expectation(ICE)本质是一样的， 在全样本上求平均也就是大家熟悉的Partial Dependence。

X-Learner

X-Learner是针对上述提到的问题对T-Learner和S-Learner进行了融合。步骤如下

1. 分别对对照组和实验组进行建模得到模型\(M_1\),\(M_2\)和T-Learner一样
2. 把对照组放进实验组模型预测，再把实验组放进对照组模型预测，预测值和实际值的差作为HTE的近似。这里和S-Learner的思路近似是imputation的做法。
3. 实验组和对照组分别对上述target建模得到\(M_3\),\(M_4\)，每个样本得到两个预测值然后加权，权重一般可选propensity score，随机实验中可以直接用进组用户数，流量相同的随机实验直接用0.5感觉也没啥问题

\[\begin{align} \hat{\mu_0}(x) &= M_1(Y^0 \sim X^0)\\ \hat{\mu_1}(x) &= M_2(Y^1 \sim X^1)\\ \hat{D_1}(x) &= Y_1 - \hat{\mu}_0(x)\\ \hat{D_0}(x) &= \hat{\mu}_1(x) - Y_0 \\ \hat{\tau_0} &= M_3(\hat{D_0}(x) \sim X_0)\\ \hat{\tau_1} &= M_4(\hat{D_1}(x) \sim X_1)\\ \hat{\tau} &= g(x) *\hat{\tau_0} + (1-g(x)) *\hat{\tau_1}\\ \end{align} \]

方法比较

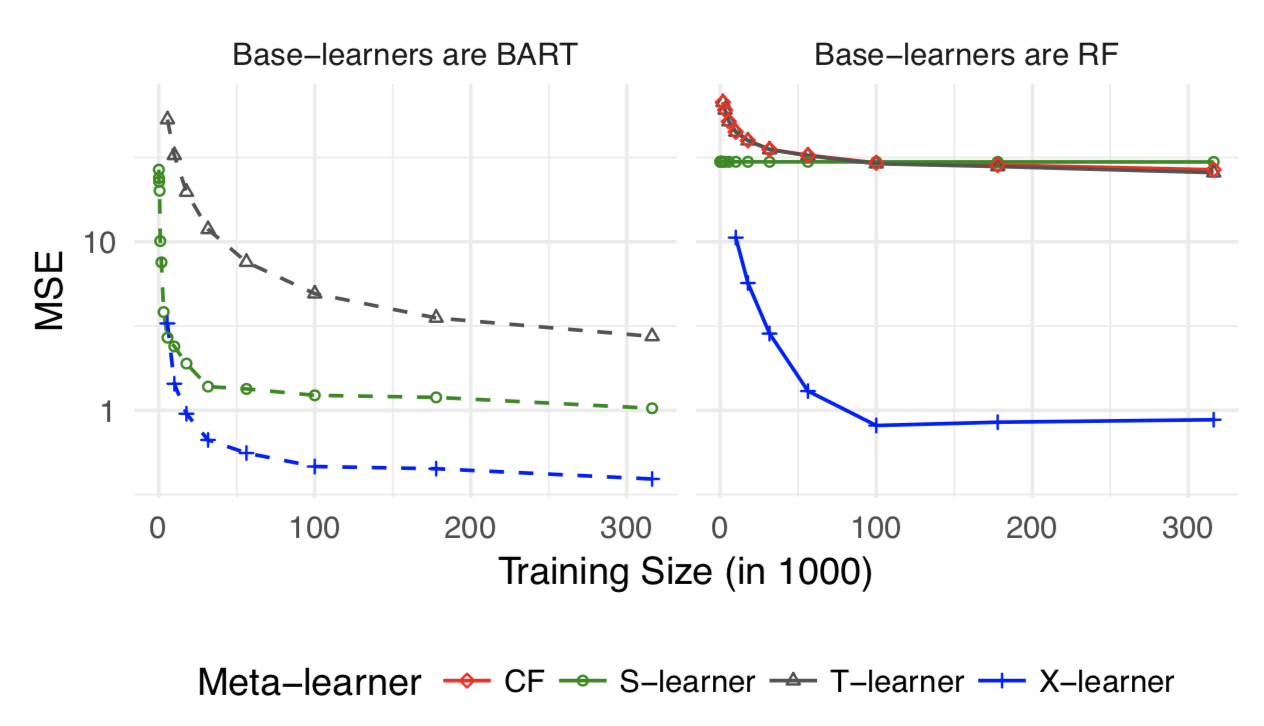
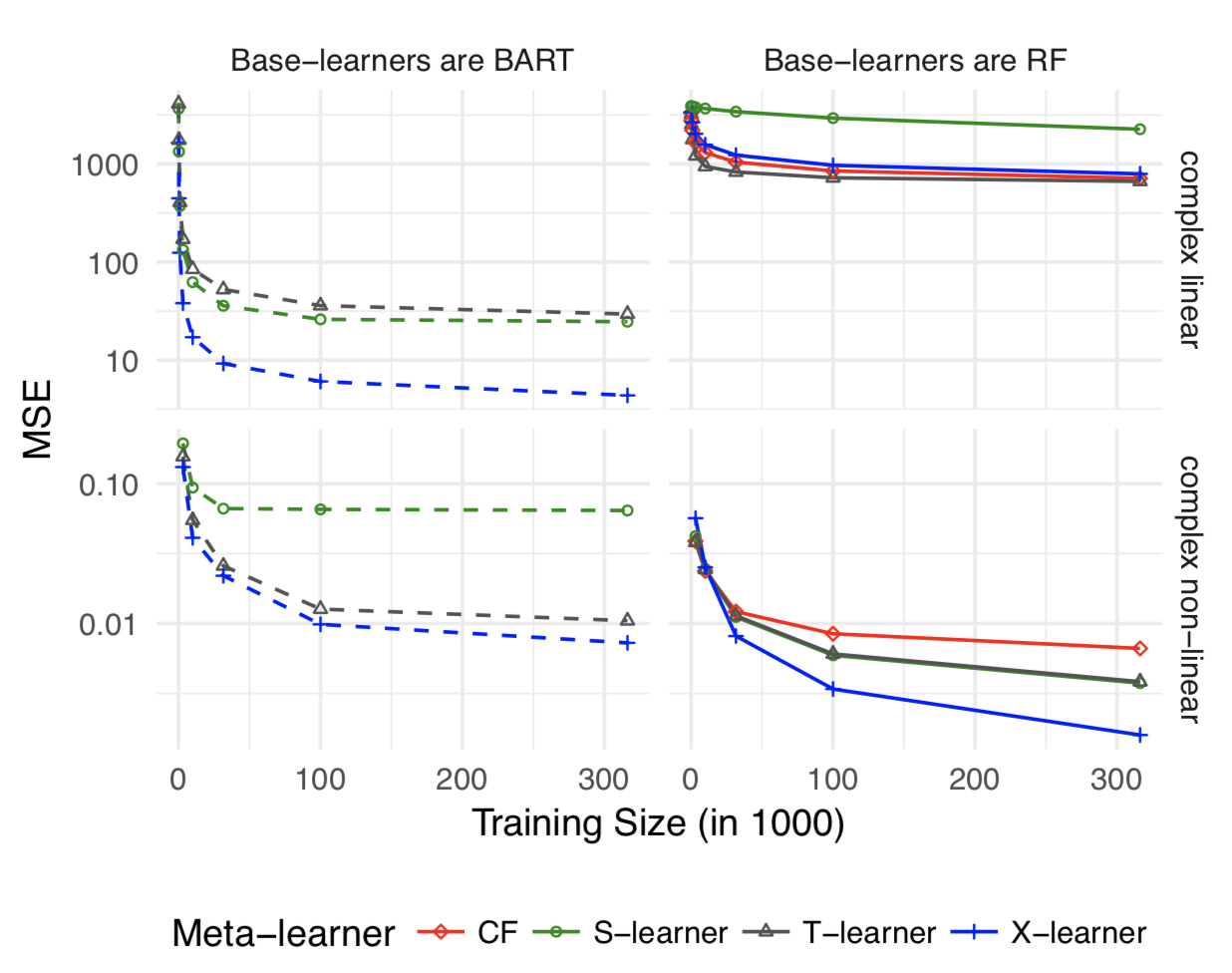
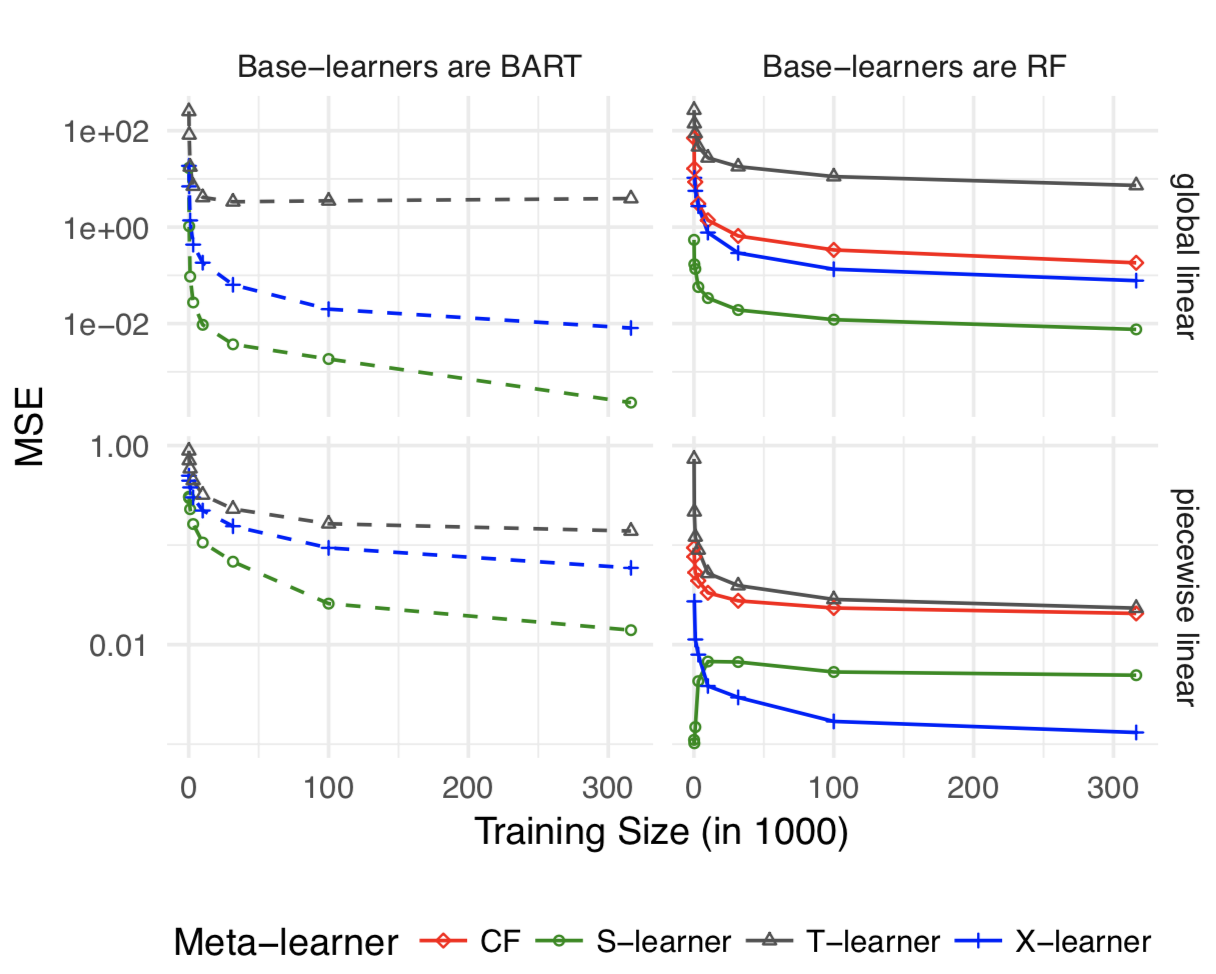
在作者分别给出几种可能类型的simulation，并评估S，X，T的表现。以下分别是：Treatment unbalanced, CATE complex linear, CATE complex non-linear, HTE=0 global linear, HTE=0 local linear。

简而言之，实验影响较大时X-Learner表现最好，实验影响微小时S-Learner和X-Learner表现差不多。

想看更多因果推理AB实验相关paper的小伙伴看过来 Paper_CausalInference_abtest

对其他HTE模型感兴趣的👇这里
因果推理的春天-实用HTE论文GitHub收藏
AB实验人群定向HTE模型1 - Causal Tree
AB实验人群定向HTE模型2 - Causal Tree with Trigger
AB实验人群定向HTE模型4 - Double Machine Learning
欢迎留言～

---

参考材料&开源代码

1. Tian L, Alizadeh AA, Gentles AJ, Tibshirani R (2014) A simple method for estimating interactions between a treatment and a large number of covari- ates. Journal of the American Statistical Association 109(508):1517–1532.
2. Powers S, et al. (2017) Some methods for het- erogeneous treatment effect estimation in high- dimensions. arXiv preprint arXiv:1707.00102.
3. Microsoft 因果推理开源代码
4. https://github.com/JasonBenn/deep-learning-paper-notes/blob/master/papers/meta-learners-for-estimating-heterogeneous-treatment-effects-using-machine-learning.md