江科大计算方法实验

实验一：插值方法

实验二：数值积分

实验三：微分方程

实验四：非线性方程

实验五：线性方程组

实验一：插值方法

一 实验目的

通过本次上机实习，能够进一步加深对各种插值算法的理解；学会使用用三种类型的插值函数的数学模型、基本算法，结合相应软件（如VC/VB/Delphi/Matlab/JAVA/Turbo C）编程实现数值方法的求解。并用该软件的绘图功能来显示插值函数，使其计算结果更加直观和形象化。

二 实验内容

通过程序求出插值函数的表达式是比较麻烦的，常用的方法是描出插值曲线上尽量密集的有限个采样点，并用这有限个采样点的连线，即折线，近似插值曲线。取点越密集，所得折线就越逼近理论上的插值曲线。本实验中将所取的点的横坐标存放于动态数组 中，通过插值方法计算得到的对应纵坐标存放于动态数组 中。
本实验将Lagrange插值、Newton插值和三次样条插值实现为一个C++类CInterpolation，并在Button单击事件中调用该类相应函数，得出插值结果并画出图像。CInterpolation类为

三 源程序清单

python 代码实现

from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist
import random
def NewTon(x, point_x, point_y):
    d = []
    n = len(point_x)
    for i in range(n):
        d.append(point_y[i])
    for k in range(1, n):
        for j in range(n-1, k-1, -1):
            d[j] = (d[j] - d[j-1])/(point_x[j]-point_x[j-k])
    p = d[n - 1]
    for i in range(n-2, -1, -1):
        p = p*(x-point_x[i])+d[i]
    return p
def lagrange(x, point_x, point_y):
    s = 0
    count = len(point_x)
    for i in range(count):
        p = 1
        for j in range(count):
            if i != j:
                p = p*(x-point_x[j])/(point_x[i]-point_x[j])
        s = s + point_y[i]*p
    return s
def main():
    point_x = [0,1,2,3,4,5]
    point_y = [0,1,8,27,64,125]
    point_x = np.array(point_x)
    point_y = np.array(point_y)
    x_list1 = []
    y_list1 = []
    for x in point_x:
        x_list1.append(x)
    for i in range(1000):
        x_list1.append(random.uniform(-5, 5))
    x_list1.sort()   # 给存放x坐标的列表排序
    for x in x_list1:
        y_list1.append(NewTon(x, point_x, point_y))

    x_list2 = []
    y_list2 = []
    for x in point_x:
        x_list2.append(x)
    for i in range(1000):
        x_list2.append(random.uniform(-5, 5))
    x_list2.sort()  # 给存放x坐标的列表排序
    for x in x_list2:
        y_list2.append(NewTon(x, point_x, point_y))

    x_list3 = []
    for x in point_x:
        x_list3.append(x)
    for i in range(1000):
        x_list3.append(random.uniform(point_x.min(), point_x.max()))
    x_list3.sort()  # 给存放x坐标的列表排序
    f = interp1d(point_x, point_y, kind='cubic')  # 编辑插值函数格式
    y_list3 = f(x_list3)
    fig = plt.figure()
    ax = axisartist.Subplot(fig, 111)
    fig.add_axes(ax)
    ax.axis[:].set_visible(False)
    ax.axis["x"] = ax.new_floating_axis(0, 0)
    ax.axis["x"].set_axisline_style("->", size=1.0)
    ax.axis["y"] = ax.new_floating_axis(1, 0)
    ax.axis["y"].set_axisline_style("-|>", size=1.0)
    ax.axis["x"].set_axis_direction("top")
    ax.axis["y"].set_axis_direction("right")
    plt.plot(x_list1, y_list1, 'g', x_list2, y_list2, 'b', x_list3, y_list3, 'y', point_x, point_y, 'or')
    plt.legend(['NewTon', 'lagrange', 'Spline', 'point'], loc='best')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
if __name__ == '__main__':
    main()

四 结果分析及心得体会

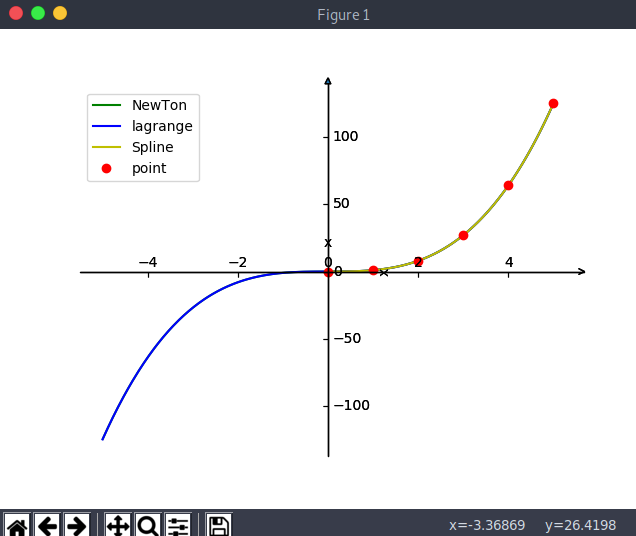
Lagrange插值法和Newton插值法解决实际问题中关于只提供复杂的离散数据的函数求值问题，通过将所考察的函数简单化，构造关于离散数据实际函数f(x)的近似函数P(x)，从而可以计算未知点出的函数值，是插值法的基本思路。
实际上Lagrange插值法和Newton插值法是同一种方法的两种变形，其构造拟合函数的思路是相同的，而实验中两个实际问题用两种算法计算出结果是相同的。
插值结点越多，三次样条插值效果越多。

实验二：数值积分

一 实验目的

通过该课程实习，学会使用数值积分的各种方法求解定积分计算的问题，体会各种方法的精度差异。

二 实验内容

本实验将梯形法的递推化和龙贝格算法编写为类CIntegration，在工程中调用该类得出积分结果并画出区间二分图像。首先画出被积函数图像，并储存被积函数在图像中每个像素对应的采样点的横坐标（存放于float型指针p_X中）和纵坐标（存放于int型指针p_Y中）；然后调用CIntegration类中相应函数，计算积分结果；最后将x轴上的区间二分点与其对应的被积函数值的点连线。
CIntegration有公有变量和指针float a,b,h,*x;int n和带参数的构造函数

三 源代码

import sys
from PyQt5.QtWidgets import QApplication, QMainWindow, QSizePolicy, QPushButton
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from matplotlib.figure import Figure
import matplotlib.pyplot as plt
import numpy as np

#显示中文和负数
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

class App(QMainWindow):
    def __init__(self):
        super().__init__()
        self.initUI()
    def initUI(self):
        self.setWindowTitle("数值积分")
        self.setGeometry(200, 50, 700, 600)
        m = Integration(self, width=7, height=6)#实例化一个画布对象
        m.move(0, 0)

        m.Romberg1()
        m.trap1()
        self.show()

#数值积分类
class Integration(FigureCanvas):
    def __init__(self, parent=None, width=5, height=4, dpi=100 ):
        fig = Figure(figsize=(width, height), dpi=dpi ,frameon=False)
        self.axes=[]
        self.axes1 = fig.add_subplot(211)
        self.axes2 = fig.add_subplot(212)
        FigureCanvas.__init__(self, fig)
        self.setParent(parent)

        FigureCanvas.setSizePolicy(self,QSizePolicy.Expanding,
                                   QSizePolicy.Expanding)
        FigureCanvas.updateGeometry(self)
        self.a=0
        self.b=6
        self.eps=0.0001
        #挪动坐标位置
        self.axes1.set_xlim(0,6)
        self.axes2.set_xlim(0,6)
        #去掉边框
        self.axes1.spines['top'].set_color('none')
        self.axes1.spines['right'].set_color('none')
        #移位置 设为原点相交
        self.axes1.xaxis.set_ticks_position('bottom')
        self.axes1.spines['bottom'].set_position(('data',0))
        self.axes1.yaxis.set_ticks_position('left')
        self.axes1.spines['left'].set_position(('data',0))
        #去掉边框
        self.axes2.spines['top'].set_color('none')
        self.axes2.spines['right'].set_color('none')
        #移位置 设为原点相交
        self.axes2.xaxis.set_ticks_position('bottom')
        self.axes2.spines['bottom'].set_position(('data',0))
        self.axes2.yaxis.set_ticks_position('left')
        self.axes2.spines['left'].set_position(('data',0))
        #初始为画图
        self.x=np.linspace(0,6)
        self.y=[self.func(i) for i in self.x]
        #self.Romberg1()

    #被积函数
    def func(self,x):
        if(x==0.0):
            return 1.0
        return np.sin(x)/x

    def getS(self,h):
        res=0
        for i in np.arange(self.a+h/2.0,self.b,h):
            res+=self.func(i)
        return res

    #变步长梯形公式
    def trap(self):
        h=self.b-self.a
        T=[]
        T.append(h * (self.func(self.a) + self.func(self.b)) /2.0)
        Tk=0
        c=[]
        while(1):
            Tk+=1
            s=self.getS(h)
            for i in np.arange(self.a+h/2.0,self.b,h):
                c.append(i-3+h*Tk)
            T.append((T[-1]+h*s)/2.0)
            if(abs(T[-1]-T[-2])<self.eps):
                break
            h/=2.0
        return (c,T[-1])
    #龙贝格算法积分
    def Romberg(self):
        k=1
        T=[]            # 复化梯形序列
        S=[0]            # Simpson序列
        C=[0]            # Cotes序列
        R=[]            # Romberg序列
        h = self.b - self.a
        T.append(h * (self.func(self.a) + self.func(self.b)) / 2.0)
        counter =0
        Rk=0
        c=[]
        while(1):
            Rk+=1
            counter+=1
            s=self.getS(h)
            T.append((T[-1]+h*s)/2.0)
            S.append((4.0*T[-1]-T[-2])/3.0)
            h/=2.0
            if(k==1):
                k+=1
            C.append((16.0*S[-1]-S[-2])/15.0)
            if(k==2):
                k+=1
            R.append((64.0*C[-1]-C[-2])/63.0)
            if(k==3):
                k+=1
            elif(abs(R[-1]-R[-2])<self.eps or counter>=100):
                break
        for i in range(1,2**Rk):
            c.append(self.a+i*(self.b-self.a)/2**Rk)
        return (c,R[-1])

    #绘制龙贝格图像
    def Romberg1(self):
        self.axes1.plot(self.x,self.y,'black',label='龙贝格')
        self.axes1.legend()#默认legend在右上方
        x,y=self.Romberg()
        #积分结果
        self.axes1.text(1,1,"result：{}".format(y))
        for i in x:
            self.axes1.plot([i,i],[0,self.func(i)], color = 'blue' ,linestyle=":")
        self.draw()

    #绘制变步长梯形
    def trap1(self):
        self.axes2.plot(self.x,self.y,'black',label='变步长')
        self.axes2.legend()#默认legend在右上方
        x,y=self.trap()
        self.axes2.text(1,1,"result：{}".format(y))#积分结果
        for i in x:
            self.axes2.plot([i,i],[0,self.func(i)], color = 'gray' ,linestyle="--")
        self.draw()
app = QApplication(sys.argv)
ex = App()
sys.exit(app.exec_())

四 实验结果及心得体会

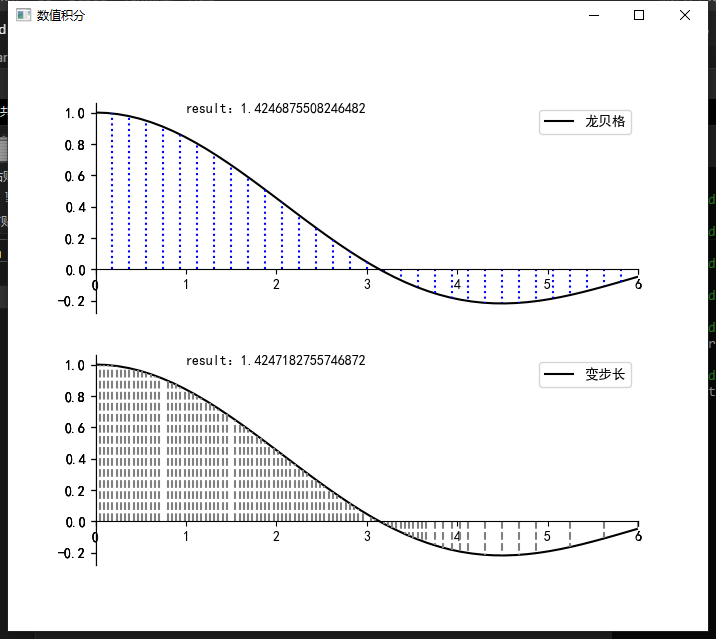
龙贝格公式是在梯形公式，辛普森公式以及柯特斯公式关系的基础上，构造出的一中加速计算积分的方法。相对于利用递推的复合梯形公式计算积分时，需要多次二分才能达到预定的精度。龙贝格积分利用外推加速可以极大的提高收敛的速度。也就是说在不增加计算量的前提下极大地提高了误差的精度。 而且龙贝格公式在计算积分时，区间不断二分，这样前一次分半以后的函数值仍然能够保存下来，可以继续利用，这一点非常利于编程。

实验三：微分方程

一 实验目的

通过本次实验，熟悉求解常微分方程初值问题的有关方法和理论，主要是欧拉法、改进欧拉法、四阶龙格库塔法，学会编制这三种方法的计算程序。体会这三种解法的功能、优缺点及适用场合。

二 实验内容

本实验将欧拉法、改进欧拉法和经典四阶龙哥库塔法编写为一个类CDifferential_Equation，调用该类实现一阶微分方程初值问题的求解，并画出解函数的图像。CDifferential_Equation的框架如下

三 源代码

import numpy as np
import matplotlib.pyplot as plt
import math
import mpl_toolkits.axisartist as axisartist


def f(x, y):
    return -y-x*y*y


def Euler(h):
    x_list = list()
    y_list = list()
    x_list.append(0)
    y_list.append(1)
    while x_list[-1] < 2:
        x_list.append(x_list[-1]+h)
        y_list.append(y_list[-1]+h*f(x_list[-2], y_list[-1]))
    show(x_list, y_list)


def Improved_Euler(h):
    x_list = list()
    y_list = list()
    x_list.append(0)
    y_list.append(1)
    while x_list[-1] < 2:
        x_list.append(x_list[-1] + h)
        y_p = y_list[-1] + h * f(x_list[-1], y_list[-1])
        y_c = y_list[-1] + h * f(x_list[-2], y_p)
        y_list.append((y_p+y_c)/2)
    show(x_list, y_list)


def Runge_Kutta(h):
    x_list = list()
    y_list = list()
    x_list.append(0)
    y_list.append(1)
    while x_list[-1] < 2:
        x_list.append(x_list[-1] + h)
        k1 = f(x_list[-2], y_list[-1])
        k2 = f(x_list[-2]+h/2, y_list[-1]+h*k1/2)
        k3 = f(x_list[-2]+h/2, y_list[-1]+h*k2/2)
        k4 = f(x_list[-1], y_list[-1]+h*k3)
        y_list.append(y_list[-1]+h*(k1+2*k2+2*k3+k4)/6)
    show(x_list, y_list)


def show(x_list1, y_list1):
    # 创建画布
    fig = plt.figure()
    # 使用axisartist.Subplot方法创建一个绘图区对象ax
    ax = axisartist.Subplot(fig, 111)
    # 将绘图区对象添加到画布中
    fig.add_axes(ax)
    ax.axis[:].set_visible(False)
    ax.axis["x"] = ax.new_floating_axis(0, 0)
    ax.axis["x"].set_axisline_style("->", size=1.0)
    ax.axis["y"] = ax.new_floating_axis(1, 0)
    ax.axis["y"].set_axisline_style("-|>", size=1.0)
    ax.axis["x"].set_axis_direction("top")
    ax.axis["y"].set_axis_direction("right")
    x_list2 = np.arange(0, 2.1, 0.1)
    y_list2 = 1/(2*math.e**x_list2-x_list2-1)
    plt.plot(x_list1, y_list1, 'r')
    plt.plot(x_list2, y_list2, 'b')
    for x in np.arange(0.125, 2.125, 0.125):
        plt.vlines(x, 0, 1/(2*math.e**x-x-1), colors='g', linestyles='dashed')
    plt.show()


if __name__ == '__main__':
    Euler(0.1)
    Improved_Euler(0.1)
    Runge_Kutta(0.1)

四 结果分析及心得体会

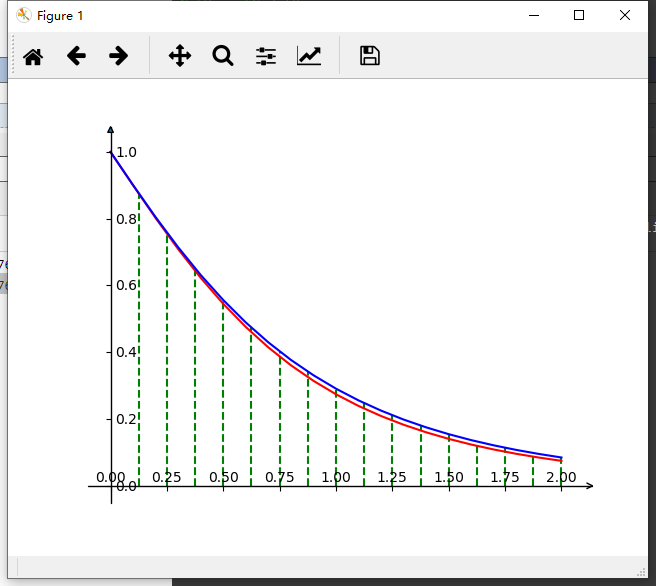
将数值解和解析解进行比较，很容易对欧拉法的三种不同算法的精度进行比较，其中改进欧拉法在这三种近似数值法的精度是最高的。欧拉法的数值求解不仅减小了数值计算的工作强度，而且提高了它的运算速度。这种方法对常微分方程初值问题的近似值求解和理论分析均具有一定的参考价值。

实验四：非线性方程

一 实验目的

通过本次实验，熟练的掌握方程求根的最基本、常用的运算方法和理论。主要有二分法、牛顿法、弦截法，并体会它们各自不同的特点及收敛速率。

二 实验内容

2.1 算法原理与底层计算程序

非线性方程f(x)=0。

（1）二分法

对于单根区间[a,b]，f(a)f(b)<0：
① 区间中点m为(a+b)/2，如果|b-a|<e,则m即为该方程的解；
② 如果f(a)=0（或f(b)=0），则a（或b）即为方程的解（注意：程序中，两浮点数不可判断相等，即使两浮点数a和b理论上相等，但“a==b;”一般不成立）；
③ 如果f(a)f(m)<0，则对区间[a,m]调用函数自身（递归），或将m赋值给b（循环），跳转①，
如果f(m)f(b)<0，则对区间[m,b]调用函数自身（递归），或将m赋值给a（循环），跳转①。

（2）牛顿法

三 源代码

import math
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist


def f(x):
    return x-2*math.sin(x)


def f1(x):
    return 1-2*math.cos(x)


def dichotomy(e):
    a = 1
    b = 3
    while abs(a-b) > e:
        if f(a) * f(b) > 0:
            print('根不在输入区间内')
            break
        c = (a + b) / 2
        if f(a)*f(c) > 0:
            a = c
        else:
            b = c

    print(a, b)


def Newton(i, e):
    x_list = list()
    x_list.append(i)
    x_list.append(x_list[-1] - f(x_list[-1]) / f1(x_list[-1]))
    while (x_list[-1]-x_list[-2]) > e:
        x_list.append(x_list[-1]-f(x_list[-1])/f1(x_list[-1]))
    print(x_list[-1])


def Chord_cut(x0, x1, e):
    x_list = list()
    x_list.append(x0)
    x_list.append(x1)
    while (x_list[-1] - x_list[-2]) > e:
        x_list.append(x_list[-1] - f(x_list[-1]) * (x_list[-1] - x_list[0]) / (f(x_list[-1]) - f(x_list[0])))
    print(x_list[-1])


def show():
    # 创建画布
    fig = plt.figure()
    # 使用axisartist.Subplot方法创建一个绘图区对象ax
    ax = axisartist.Subplot(fig, 111)
    # 将绘图区对象添加到画布中
    fig.add_axes(ax)
    ax.axis[:].set_visible(False)
    ax.axis["x"] = ax.new_floating_axis(0, 0)
    ax.axis["x"].set_axisline_style("->", size=1.0)
    ax.axis["y"] = ax.new_floating_axis(1, 0)
    ax.axis["y"].set_axisline_style("-|>", size=1.0)
    ax.axis["x"].set_axis_direction("top")
    ax.axis["y"].set_axis_direction("right")
    x_list = np.arange(0, 4, 0.1)
    x_list = list(x_list)
    y_list = list()
    for x in x_list:
        y_list.append(f(x))
    plt.plot(x_list, y_list, 'b')
    plt.vlines(1, 0, 1-2*math.sin(1), colors='g', linestyles='dashed')
    plt.vlines(3, 0, 3-2*math.sin(3), colors='g', linestyles='dashed')
    plt.show()


if __name__ == '__main__':
    #dichotomy(0.001)
    #Newton(1.9, 0.0001)
    #Chord_cut(1.8, 1.9, 0.0001)
    show()

四 结果分析及心得体会

二分法能达到较好的精度，但当所求问题较为庞大且对其根的估计范围宽泛时，二分法需迭代的步数很大。
牛顿迭代法是二次收敛的，因此牛顿迭代法求解非线性方程的解，迭代次数较小，能以较小的计算量和较小的空间利用得到相对精确的数值解。但其缺点为需要所求非线性方程的导函数值，所以一适用范围相对较小，只能对一阶可导的方程进行迭代。
快速弦截法步入牛顿收敛速度快，但比二分法要快的多，可以达到相对较高的精度。

实验五：线性方程组

一 实验目的

通过本课程的实习，学会编写全主元消去法的计算程序。掌握解线性方程组的最基本算法及其运用，进一步了解该解法的功能、优缺点，领会系数矩阵对解的影响。

二 实验内容

求解n元线性方程组

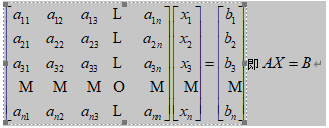
三 源代码

import numpy as np
 
 
def getInput1():
    matrix_a = np.mat([[0.726, 0.81, 0.9],
                       [1, 1, 1],
                       [1.331, 1.21, 1.1]
                       ], dtype=float)
    matrix_b = np.mat([0.6867, 0.8338, 1])
    # 答案：-2 0 1 1
    return matrix_a, matrix_b
 
 
# 设置矩阵
def getInput():
    matrix_a = np.mat([[2, 3, 11, 5],
                     [1, 1, 5, 2],
                     [2, 1, 3, 2],
                     [1, 1, 3, 4]], dtype=float)
    matrix_b = np.mat([2, 1, -3, -3])
    # 答案：-2 0 1 1
    return matrix_a, matrix_b
 
 
# 交换
def swap(mat, num):
    print(num)
    print("调换前")
    print(mat)
    maxid = num
    for j in range(num, mat.shape[0]):
        if mat[j, num] > mat[num, num]:
            maxid = j
    if maxid is not num:
        mat[[maxid,num],:] = mat[[num,maxid],:]
    else:pass
    print("调换后")
    print(maxid)
    print(mat)
    return mat
 
 
def SequentialGauss(mat_a):
    for i in range(0, (mat_a.shape[0])-1):
        swap(mat_a, i)
        if mat_a[i, i] == 0:
            print("终断运算：")
            print(mat_a)
            break
        else:
            for j in range(i+1, mat_a.shape[0]):
                mat_a[j:j+1 , :] = mat_a[j:j+1,:] - \
                                                    (mat_a[j,i]/mat_a[i,i])*mat_a[i, :]
    return mat_a
 
 
# 回带过程
def revert(new_mat):
    # 创建矩阵存放答案 初始化为0
    x = np.mat(np.zeros(new_mat.shape[0], dtype=float))
    number = x.shape[1]-1
    # print(number)
    b = number+1
    x[0,number] = new_mat[number,b]/new_mat[number, number]
    for i in range(number-1,-1,-1):
        try:
            x[0, i] = (new_mat[i,b]-np.sum(np.multiply(new_mat[i,i+1:b],x[0,i+1:b])))/(new_mat[i,i])
        except:
            print("错误")
    print(x)
 
 
if __name__ == "__main__":
    mat_a, mat_b = getInput()
    # 合并两个矩阵
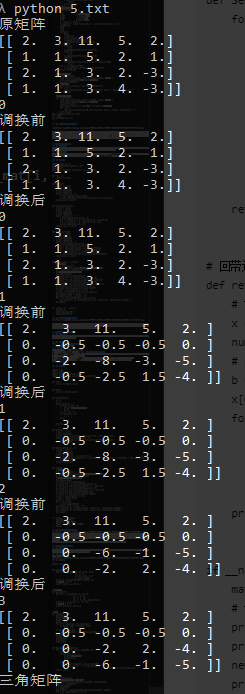
    print("原矩阵")
    print(np.hstack((mat_a, mat_b.T)))
    new_mat = SequentialGauss(np.hstack((mat_a, mat_b.T)))
    print("三角矩阵")
    print(new_mat)
    print("方程的解")
    revert(new_mat)

四 结果分析及心得体会

这种算法是对约当消去法的一种改进，这种改进明显的减少了计算量，而回代过程的计算量可以忽略不计，因此，它比约当消去法大约节省了50%的计算量。 但由于添加了回代过程，算法的结构较约当法稍复杂。在用高斯消去法求解一般的线性方程时，如果其绝对值很小，舍入误差的影响也会严重的损失精度，实际计算时要尽量避免这类情况的发生。