信息检索导论学习笔记(7)-文档评分、词项权重计算
文档评分、词项权重计算
迄今为止,我们介绍了支持布尔查询的索引处理办法,给定一个布尔查询,一篇文档要么满足查询的要求要么不满足(布尔查询是一种非黑即白的处理方式)。因此对布尔查询常常会导致过少(=0)或者过多(>1000)的结果。因此要对搜索结果进行排序,那么如何设计排序算法呢?
集合重合度
对查询进行数学建模,采用jaccard系数计算两个集合重合度的,根据jaccard系数对搜索结果进行排序。
实例:查询“ides of March”,文档“Caesar died in March”。集合A={ides of March},B={ides of March Caesar died in},JACCARD(q, d) = 1/6
注:考虑文档的长度因素,我们可以使用余弦计算(如上图)来代替|A ∩ B|/|A∪B| ,前者进行了长度归一化处理。
jaccard系数的不足:
- 不考虑词项频率,即词项在文档中的出现次数。
- 罕见词比高频词的信息量更大,Jaccard系数没有考虑这个信息。
词项频率及权重计算
现在开始考虑词项频率,按常理如果文档或者域中词项出现的频率越高,那么该文档或者域的得分也越高。
词项频率:词项t的词项频率tft,d 是指t在d中出现的次数(其中的两个下标分别对应词项和文档)。
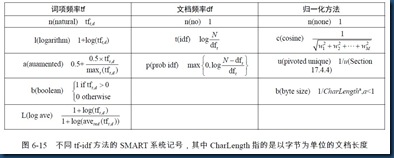
那么如何评价得分呢?最简单的方式是直接根据term在文档中的出现次数(即原始词频tf),来对文档进行评分。
然而原始tf不太合适:某个词项在A文档中出现十次,即tf = 10,在B文档中tf = 1,那么A比B更相关,但是相关度不会相差10倍,相关度不会正比于词项频率tf。
一种替代原始tf的方法: 对数词频
公式中的数字1是为了平滑计算用的,对于tf值为1的情况,采用对数词频加1的方式进行平滑处理。
另一种tf的变体计算公式:基于最大值的tf归一化
这种方法被称为增强型规范化tf,其中的a是调节因子,过去经验取值0.5,新的研究表明取值为0.4效果更好。公式中的tf代表这个单词的实际词频数目,而Max(tf)代表了文档中所有单词中出现次数最多的那个单词对应的词频数目。之所以要如此操作,主要对于对长文档的一种抑制,因为如果文档较长,则长文档中所有单词的tf值会普遍比短文档的值高,但是这并不意味这长文档与查询更相关。用单词实际词频除以文档中最高词频,等于将绝对的数值进行了规范化转换,公式的含义就转换为:同一个文档内单词之间的相对重要性。
逆文档频率idf
文档中所有词项的重要性是一样的吗?答案显然是否定的。(tf的计算方法未考虑此问题)
显然罕见词项比常见词所蕴含的信息更多。因此在对搜索结果排序时,对于罕见词项我们希望赋予高权重而对于常见词我们希望赋予正的低权重。
引入因子文档频率(document frequency)df,它表示的是出现 t的所有文档的数目。
如上述 罕见词项比常见词所蕴含的信息更多,因此df是和词项t的信息量成反比的一个值。由于df 本身往往较大,所以通常需要将它映射到一个较小的取值范围中去。于是定义词项t的逆文档因子idf(其中N 是文档集中文档的数目)。
idf是反映词项t的信息量的一个指标,一个罕见词的idf 往往很高,而高频词的idf 就可能较低。值得注意的是,对于tf 和idf我们都采用了对数计算方式。
idf对排序的影响
- idf会影响至少包含2个词项的查询的文档排序结果。例如,在查询“arachnocentric line”中, idf权重计算方法会增加arachnocentric的相对权重,同时降低line的相对权重。
- 对于单词项查询,idf对文档排序基本没有任何影响。
tf-idf权重计算
对于每篇文档中的每个词项,可以将其tf和idf组合在一起形成最终的权重。tf-idf权重机制对文档d中的词项t赋予的权重如下:
换句话说,tf-idf按照如下的方式对文档d中的词项t赋予权重:
- 当t只在少数几篇文档中多次出现时,权重取值最大(此时能够对这些文档提供最强的区分能力);
- 当t在一篇文档中出现次数很少,或者在很多文档中出现,权重取值次之(此时对最后的相关度计算作用不大) ;
- 如果t在所有文档中都出现,那么权重取值最小。
tf-idf权重计算的一些变型
posted on 2012-08-20 16:18 God bless you 阅读(3985) 评论(0) 收藏 举报

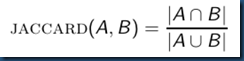
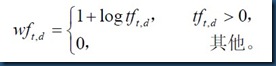
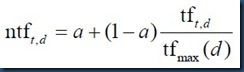
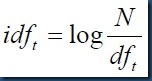


 浙公网安备 33010602011771号
浙公网安备 33010602011771号