信息检索导论学习笔记(3)
词典及容错式检索
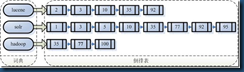
如上图,倒排索引记录表构建好后。对于查询请求“solr”,我们的首要任务是确定查询词项solr是否在词典的词项词汇表中,如果在,则返回该词项对应的倒排记录表的指针。如何在数据结构(即词典)中快速定位词项?
词典(即存储词项词汇表的数据结构)
快速定位词项主要有两大类解决方案
哈希表方式
每个词项通过哈希函数映射成一个整数,映射函数的目标空间需要足够大,以减少哈希结果冲突的可能性。查询时,对于每个查询项分别进行哈希操作,并解决存在的冲突,最后返回每个查询词项对应的倒排记录表的指针。
优点:在哈希表中的定位速度快于树中的定位速度,查询时间是常数
缺点:
没办法处理词项的微小变形(resume vs. résumé)
不支持前缀搜索(比如所有以automat开头的词项)
如果词汇表不断增大,需要定期对所有词项重新哈希
搜索树方式(二叉树及B树)
优点:支持前缀查询
缺点:搜索速度略低于哈希表方式: O(logM), 其中M 是词汇表大小,即所有词项的数目。O(logM) 仅仅对平衡树成立
词典数据结构的选取要综合考虑
- 词项的数目有多少?
- 词项的数目是固定的还是经常变化?在变化的情况下,是只插入新词项,还是同时要删除某些旧词项?
- 不同词项的相对访问频率如何?
通配符查询
B树结构词典通配符查询处理
- 对mon*的查询操作,遍历B-树结构,返回区间mon ≤ t< moo上的词项term
- 对*mon的查询操作,遍历反向B-树结构,返回区间nom ≤ t < non上的词项term
- 对m*nchen的查询操作,在B‐树中分别查找满足m*和*nchen的词项集合,然后求交集
然而对于上述一般通配查询的操作,开销太大。
轮排(permuterm) 索引(称为轮排树更恰当)
基本思想:
首先我们在字符集中引入一个新的符号$,用于标识词项结束。
将每个通配查询旋转,使*出现在末尾。
将每个旋转后的结果存放在词典(B‐树)中。即对词典中的词项词汇表再进行了一层索引
对于词项hello: 将hello$, ello$h, llo$he, lo$hel, 和o$hell 加入到B‐树中,其中$ 是一个特殊符号。
考虑通配符查询 m*n, 这里的关键是将查询进行旋转让*号出现在字符串末尾,即得到 n$m* 。下一步,在轮排索引中查找该字符串(可通过搜索树方式查找) ,实际上等价于查找某些词项(如 man和 moron)的旋转结果。
问题:相对于通常的B‐树,轮排树的空间要大4倍以上(经验值)
k‐gram 索引(比轮排索引空间开销要小,但可能要进行后过滤)
一个 k-gram代表由k个字符组成的序列。对于词项 castle来说,cas、ast、stl都是 3-gram。我们用一个特殊的字符$来标识词项的开始或者结束,因此对于 castle来说,所有的 3-gram包括$ca、cas、ast、stl、tle及 le$。
构建基本思想:
首先我们在字符集中引入一个新的符号$,用于标识词项开始和结束。
枚举一个词项中所有连读的k个字符构成的k‐gram ,将所有的k-gram建立倒排索引。即对词典中的词项词汇表再进行了一层索引
对2-gram索引来说,查询mon* 可以先执行布尔查询: $m AND mo AND on,该布尔查询会返回所有以前缀mon开始的词项,当然也可能返回许多伪正例,比如MOON。 因此,必须要做后续的过滤。处理余下的词项将在词项‐文档倒排索引中查找文档,最终完成通配符查询操作。
注:即使没有通配符查询的布尔组合,单个通配符查询的处理也是非常耗时的,除了最后要在词项‐文档倒排索引中查找之外,还要在特定索引(如轮排索引或 k-gram索引)中进行查找、在结果中进行过滤等操作。搜索引擎可以支持这些丰富的功能,但是搜索引擎通常将这些功能隐藏在一个大部分用户从不访问的界面(如“ 高级搜索” 界面)下。如果把这些功能暴露在一般搜索界面上,用户常常会受鼓励而使用这些功能,即便在他们不是特别需要的时候(比如,输入以a*开始的查询的前缀) ,这样就会大大增加搜索引擎的负担。
拼写校正
用途:
- 纠正待索引文档。在IR领域, 我们主要对OCR处理后的文档进行拼写校正处理. (OCR = optical character recognition,光学字符识别)。IR领域的一般做法是:不改变文档
- 纠正用户的查询
方法:
- 词独立(Isolated word)法:只检查每个单词本身的拼写错误。如果某个单词拼写错误后变成另外一个单词,则无法查出。e.g., an asteroid that fell form the sky
- 上下文敏感(Context‐sensitive)法:纠错时要考虑周围的单词,能纠正上例中的错误form/from
词独立(Isolated word)法
解决该问题常分两个步骤:
1.在给定词项词汇表 V 和查询字符串 q,我们要从 V 中寻找和 q具有最小编辑距离的字符串,得到候选的“正确”单词词汇表。
2.为了进一步限制计算编辑距离后得到的词汇表大小,常通过使用k-gram索引来辅助返回与查询 q具有较小编辑距离的词项。
步骤1中词汇表V的几种选择方式:
- 采用标准词典(韦伯词典, 牛津词典等等)
- 采用领域词典(面向特定领域的IR系统)
- 采用文档集上的词项词汇表,但是每个词项均带有权重
编辑距离(edit distance)的计算方法:Levenshtein distance算法(非常经典的一个动态规划算法)
Levenshtein distance
wiki地址:http://en.wikipedia.org/wiki/Levenshtein_distance
java语言开源实现:http://commons.apache.org/lang/
/**
* StringUtils.getLevenshteinDistance(null, *) = IllegalArgumentException
* StringUtils.getLevenshteinDistance(*, null) = IllegalArgumentException
* StringUtils.getLevenshteinDistance("","") = 0
* StringUtils.getLevenshteinDistance("","a") = 1
* StringUtils.getLevenshteinDistance("aaapppp", "") = 7
* StringUtils.getLevenshteinDistance("frog", "fog") = 1
* StringUtils.getLevenshteinDistance("fly", "ant") = 3
* StringUtils.getLevenshteinDistance("elephant", "hippo") = 7
* StringUtils.getLevenshteinDistance("hippo", "elephant") = 7
* StringUtils.getLevenshteinDistance("hippo", "zzzzzzzz") = 8
* StringUtils.getLevenshteinDistance("hello", "hallo") = 1
*/
注:对查询字符串q在V中穷举计算编辑距离的代价会很大,实际当中往往通过启发式策略提高查找效率
k-gram 重合度(k-gram overlap)
在步骤1计算编辑距离后得到的词汇表中,利用k‐gram索引返回能够匹配很多查询k‐gram的正确单词。匹配程度(数目或者指标)上可以事先设定阈值。E.g., 比如最多只有3 个k‐gram不同。
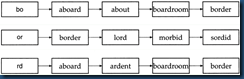
对上图(计算编辑距离后得到的词汇表),和查询字符串 bord存在至少两个 2-gram 的匹配词汇为aboard、boardroom及 border
上下文敏感的拼写校正
独立的词项拼写校正方法在面对诸如flew form Heathrow 中的输入错误时无能为力,因为这3个词单独看来拼写都没有错误。当输入这类查询时,搜索引擎可能会发现返回的文档非常少, 随后也许会提供正确的查询建议 flew from Heathrow。 这种功能的一种简单的实现方法就是,即使每个单词拼写都是对的,仍然要对每个单词找到可能的拼写正确词(Levenshtein、k-gram 重合度方法) ,然后尝试对短语中的每个词进行替换。比如对于上面 flew form Heathrow的例子,我们可能会返回如下短语 fled from Heathrow和 flew fore Heathrow。对每个替换后的短语,搜索引擎进行查找并确定最后的返回数目。
如果单独的查询有多种可能的正确拼写形式,那么上述方法中穷举过程的开销会非常大,最后我们就会面对非常多的拼写组合。有一些启发式方法可以减小可能的拼写结果空间。上述例子中,当我们对 flew 及 from 进行扩展时,我们只保留文档集合或查询日志中的高频组合结果。比如,我们很可能会保留 flew from而不是 fled fore或 flea form,这是因为 fled fore很可能比 flew from出现的次数少。接下来,我们仅仅根据高频双词(如 flew from)来获得 Heathrow的可能的正确拼写。计算双词频率的时候可以使用文档集,也可以使用用户的查询日志。
基于发音的校正技术
在IR中并不非常普遍,主要用于人名及专有名词的语音校正。适用于“高召回率”任务(e.g., 国际刑警组织Interpol在全球范围内追查罪犯)
soundex算法
wiki地址:http://en.wikipedia.org/wiki/Soundex
java语言开源实现:http://commons.apache.org/codec/
posted on 2012-08-13 12:48 God bless you 阅读(4203) 评论(3) 编辑 收藏 举报