面向对象程序设计第一单元总结
一、思路分析/总结
第一单元的三次作业可以说是在不同的限制之下做同一件事情:化简表达式。我的思路和方法也因此在同一个框架上进行不断的迭代。
总的来说,我使用的方法类似于递归下降/表达式树/分治,即将输入的一行表达式层层化简,从最复杂的表达式,再到项,再到因子,不断地递归解决子问题,再合并子问题得到答案。这三次作业的数据限制逐渐减少,而我的程序的框架可以说是完全没有改变,这是一种架构的优势,但反思之后我觉得这也有一定的缺点。
简要算法
一个合法的表达式,应当被解析成一个类实例,这个类实例的成员状态能完整且唯一地刻画这个表达式,之后可以使用toString函数输出。
事实上一个项或者一个因子都可以被看作是一个表达式,本程序中所有的表达式、项、因子都将被解析成一个表达式状态的类实例,其类名为Xpression。
根据表达式形式化的表述,需要用三种解析方法:解析表达式-parseExp,解析项-parseEntry,解析因子-parseFactor.
- 读入数据:
- 对于输入的自定义函数,进行预处理并保存
- 对于输入的表达式,直接输入到解析表达式的函数
parseExp
- 解析表达式
parseExp:- 找到优先级最小的运算符将算式分成两部分(表达式|项)
- 一部分递归解析,一部分用
parseEntry解析 - 合并结果
- 解析项
parseEntry:- 找到优先级最小的运算符将算式分成两部分(项|因子)
- 一部分递归解析,一部分用
parseFactor解析 - 合并结果
- 解析因子
parseFactor:- 对于所有可能的情况,直接解析(可能用到
parseExp)并返回
- 对于所有可能的情况,直接解析(可能用到
二、迭代开发过程&程序结构
思路如前一节中所示,在这三次作业中,迭代开发的关键因素在于如何刻画一个表达式的内容。
第一次作业
迭代开发
第一次作业中,任何表达式的计算结果可以简单地用一个“幂函数之和”来刻画。我的实现思路是,对于任何一个表达式类,使用一个哈希表来刻画。这个哈希表的键值对可以表述为<幂次,对应系数>。
结构分析

度量分析
| method | CogC | Ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Xpression.toString() | 42.0 | 6.0 | 5.0 | 14.0 |
| Tree.parseExp(String) | 28.0 | 5.0 | 10.0 | 15.0 |
| Tree.parseEntry(String) | 18.0 | 4.0 | 9.0 | 13.0 |
| Tree.parseFactor(String) | 8.0 | 7.0 | 4.0 | 8.0 |
| Tree.checkBracket(String) | 6.0 | 5.0 | 3.0 | 6.0 |
| Xpression.Xpression(int, String) | 3.0 | 1.0 | 4.0 | 4.0 |
| Xpression.multiply(Xpression) | 3.0 | 1.0 | 3.0 | 3.0 |
| Xpression.add(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Xpression.sub(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Xpression.negative() | 1.0 | 1.0 | 2.0 | 2.0 |
| Tree.main(String[]) | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.Xpression(HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 113.0 | 34.0 | 48.0 | 73.0 |
| Average | 9.416666666666666 | 2.8333333333333335 | 4.0 | 6.083333333333333 |
第二次作业
迭代开发
第二次作业加入了自定义函数,三角函数和求和函数。自定义函数和求和函数比较好处理:在遇到时使用替换,之后递归解决。而三角函数带来的问题是,前一次作业的类结构已经无法刻画一个表达式的状态了。
这次作业中我使用了略带“强行/暴力”的方法来表示一个表达式的状态(这一点问题很大,导致在第三次作业中迭代开发时,表达表达式状态的思路走到了绝境)。
对于每个表达式类Xpression,它应该是一系列乘积(即“项”)之和。用另一个类Item来作为哈希表的键,对应系数作为值。 Item类代表的就是一个个不可合并的项,例如:x*sin(x)*sin(x**2)*cos(x) 和x**2 * cos(x**3) 都代表Item。 而在Item类中又用两个哈希表和一个变量,来刻画x的幂次,sin的乘积子结构和cos的乘积子结构。可以说这已经比较勉强了,确实不太优雅。
在底层的复杂表示之上,这次作业的结构仍然提供了和前一次作业相同的抽象接口,即表达式合并和输出。对于表达式和项的解析,可以说是完全没有改变;而对于因子的解析则只需增加对应的对自定义函数和求和函数的处理。
结构分析
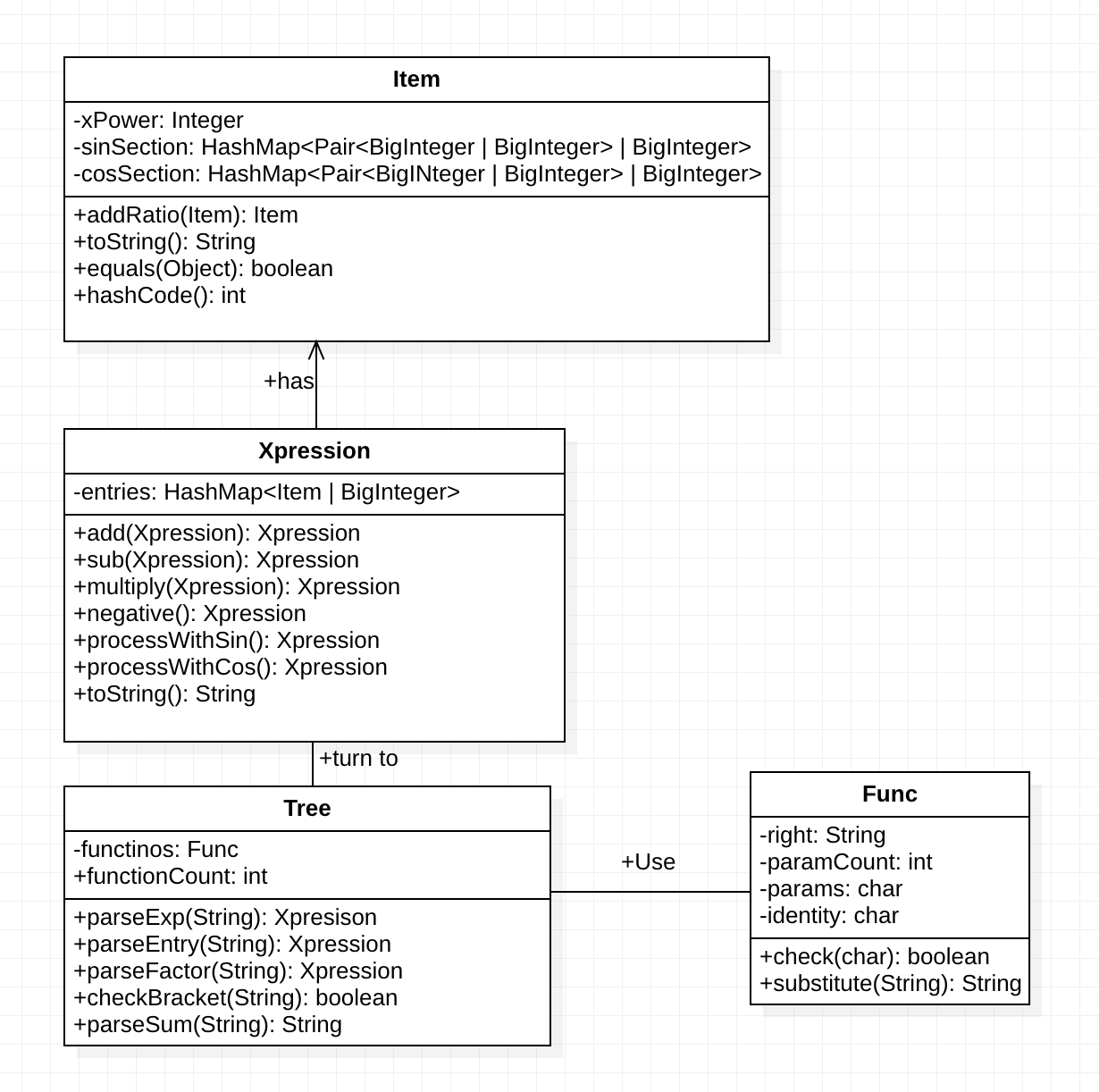
度量分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Item.toString() | 36.0 | 3.0 | 7.0 | 18.0 |
| Tree.parseExp(String) | 28.0 | 5.0 | 10.0 | 15.0 |
| Tree.parseFactor(String) | 25.0 | 14.0 | 15.0 | 20.0 |
| Xpression.toString() | 19.0 | 6.0 | 7.0 | 12.0 |
| Tree.parseEntry(String) | 18.0 | 4.0 | 9.0 | 13.0 |
| Func.substitute(String) | 16.0 | 4.0 | 9.0 | 11.0 |
| Tree.parseSum(String) | 13.0 | 2.0 | 8.0 | 10.0 |
| Tree.checkBracket(String) | 8.0 | 5.0 | 3.0 | 7.0 |
| Func.Func(String) | 4.0 | 1.0 | 4.0 | 4.0 |
| Item.addRatio(Item) | 4.0 | 1.0 | 5.0 | 5.0 |
| Item.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| Xpression.Xpression(int, String) | 3.0 | 1.0 | 4.0 | 4.0 |
| Xpression.multiply(Xpression) | 3.0 | 1.0 | 3.0 | 3.0 |
| Item.Item(int, Integer) | 2.0 | 1.0 | 1.0 | 3.0 |
| Xpression.add(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Xpression.sub(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Item.onlyConstant() | 1.0 | 1.0 | 3.0 | 3.0 |
| Tree.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| Xpression.negative() | 1.0 | 1.0 | 2.0 | 2.0 |
| Xpression.processWithCos() | 1.0 | 1.0 | 2.0 | 2.0 |
| Xpression.processWithSin() | 1.0 | 1.0 | 2.0 | 2.0 |
| Func.check(char) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.Item(Integer, HashMap, BigInteger>, HashMap, BigInteger>) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.cosed(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.sined(BigInteger) | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.Xpression(HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 192.0 | 64.0 | 112.0 | 154.0 |
| Average | 7.111111111111111 | 2.3703703703703702 | 4.148148148148148 | 5.703703703703703 |
第三次作业
迭代开发
这一次作业让之前“直接状态表示”的思路完全无法处理了,不可能用有限个简单的哈希表来刻画一个表达式。但是柳暗花明又一村,表达式由因子组成,因子又由表达式组成,我采用了交叉解析的思路:
之前的Xpression类使用以Item作为键值的哈希表,而Item类仍然使用哈希表来刻画sin和cos部分,不过Item类中哈希表的键值又是原来的Xpression类。即:一个表达式的状态经过一条链:Xpreesion - Item - Xpression 无穷无尽地刻画下去,最终到达没有三角函数的最简单表达式:幂函数或者常量作为出口。
也就是说,在这次作业中,整体的框架仍然完全没有改变,不过我将底层的状态描述由静态的表描述改成了递归的链来描述,而上层接口不需要任何变化。
结构分析

度量分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Func.check(char) | 0.0 | 1.0 | 1.0 | 1.0 |
| Func.Func(String) | 4.0 | 1.0 | 4.0 | 4.0 |
| Func.substitute(String) | 16.0 | 4.0 | 9.0 | 11.0 |
| Item.addRatio(Item) | 4.0 | 1.0 | 5.0 | 5.0 |
| Item.equals(Object) | 4.0 | 3.0 | 4.0 | 6.0 |
| Item.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.Item(BigInteger, HashMap, HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| Item.Item(int, BigInteger) | 2.0 | 1.0 | 1.0 | 3.0 |
| Item.Item(int, Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Item.onlyConstant() | 1.0 | 1.0 | 3.0 | 3.0 |
| Item.toString() | 12.0 | 1.0 | 4.0 | 9.0 |
| Tree.checkBracket(String) | 8.0 | 5.0 | 3.0 | 7.0 |
| Tree.main(String[]) | 1.0 | 1.0 | 2.0 | 2.0 |
| Tree.parseEntry(String) | 18.0 | 4.0 | 9.0 | 13.0 |
| Tree.parseExp(String) | 28.0 | 5.0 | 10.0 | 15.0 |
| Tree.parseFactor(String) | 25.0 | 14.0 | 15.0 | 20.0 |
| Tree.parseSum(String) | 13.0 | 2.0 | 8.0 | 10.0 |
| Xpression.add(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Xpression.equals(Object) | 3.0 | 3.0 | 2.0 | 4.0 |
| Xpression.hashCode() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.multiply(Xpression) | 3.0 | 1.0 | 3.0 | 3.0 |
| Xpression.negative() | 1.0 | 1.0 | 2.0 | 2.0 |
| Xpression.processWithCos() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.processWithSin() | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.sub(Xpression) | 2.0 | 1.0 | 3.0 | 3.0 |
| Xpression.toString() | 19.0 | 6.0 | 7.0 | 12.0 |
| Xpression.Xpression(HashMap) | 0.0 | 1.0 | 1.0 | 1.0 |
| Xpression.Xpression(int, String) | 3.0 | 1.0 | 4.0 | 4.0 |
| Xpression.Xpression(Item) | 0.0 | 1.0 | 1.0 | 1.0 |
| Total | 171.0 | 66.0 | 112.0 | 150.0 |
| Average | 5.896551724137931 | 2.2758620689655173 | 3.8620689655172415 | 5.172413793103448 |
三、Bug分析
我的Bug
非常庆幸,由于我结构的一致性,我没有在表达式解析部分上出现任何Bug。第一次和第三次的作业均通过了所有强测。
在第二次作业的强测中,我在输出表达式状态上出现了一些问题,在表达式比较简单,Item项不是复杂乘积的时候(如简单的一个常数或者一个三角函数项),可能导致输出被忽略。(这是一个与架构关系不太大的问题……主要原因在于对于各式各样的输出可能,逻辑上考虑的不够全面)
在这个点上我感受颇深:第一次作业比较容易,我“舍近求远”,搭建了一个可以解析任意多括号的架构,而在之后的迭代中,却因此获得了好处,让我不用担心程序整体框架的逻辑(接口和接口之间的联系)是否有问题,只需要修改底层的数据表示方法即可。
发现别人的Bug
由于我自己的问题主要出现在输出方面,我对互测的想法是从边界情况入手,如sin(0), sin(-1);构造求和函数的特殊情况;构造大整数……
其他想法:个人觉得用太多的时间来测量别人的程序的行为中,趣味性、竞技性比较强,类似于零和博弈。如果想要学习其他人的面向对象编程思路,我们其实也可以去用这些时间阅读一些开源项目的代码,或是看一本经典的书。编程当然是快乐的,个人认为学习到更前沿的东西比“为了得分刀掉身边的同学”更让人快乐。
四、体验和总结
虽然这几次作业对我来说都比较顺利,但是我觉得我的代码确实还不够“OO”。有点像是在算法题上强行填入了面向对象的元素。例如我在Tree主类里放了几个函数,这其实是不太好的,也许建立一个“解析器”类是更好的原则。总的来说,我主要是把“表达式和相关的状态变换”用面向对象的思想处理了,但是在解析表达式的流程上还是不够“面向对象”。
一部分原因是以“解决问题为导向”的话,越简单和面向过程的架构会更简便。为了培养自己构建工程框架的能力,在剩余几次的作业中还是应该尽可能的OO一点。希望能有机会用面向对象的思想来建立一个更工程化(Less算法)的程序系统。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号