在机器学习的特征选择中，利用选择矩阵的范数对选择矩阵进行约束，即是正则化技术，是一种稀疏学习。
矩阵的L0,L1范数
为了度量稀疏矩阵的稀疏性，则定义矩阵的一种范数，为： ∥W∥1=∑i,j|Wi,j|。即为矩阵所有元素的绝对值之和，能够描述接矩阵的稀疏性，但是在优化时，难度较大，是将情况向矩阵中元素尽可能是0的方向优化。
1）L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0。换句话说，让参数W是稀疏的。
2）L1范数是指向量中各个元素绝对值之和。L1范数是L0范数的最优凸近似。任何的规则化算子，如果他在Wi=0的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。W的L1范数是绝对值，|w|在w=0处是不可微。
3）虽然L0可以实现稀疏，但是实际中会使用L1取代L0。因为L0范数很难优化求解，L1范数是L0范数的最优凸近似，它比L0范数要容易优化求解。
矩阵的L2范数
L2范数，又叫“岭回归”（Ridge Regression）、“权值衰减”（weight decay）。它的作用是改善过拟合。过拟合是：模型训练时候的误差很小，但是测试误差很大，也就是说模型复杂到可以拟合到所有训练数据，但在预测新的数据的时候，结果很差。
L2范数是指向量中各元素的平方和然后开根。我们让L2范数的规则项||W||2最小，可以使得W的每个元素都很小，都接近于0。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。
L1是绝对值最小，L2是平方最小：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。
矩阵的L2,1范数
而为了进一步说明矩阵的稀疏性，来说明特征选择中矩阵L2,1范数的作用。
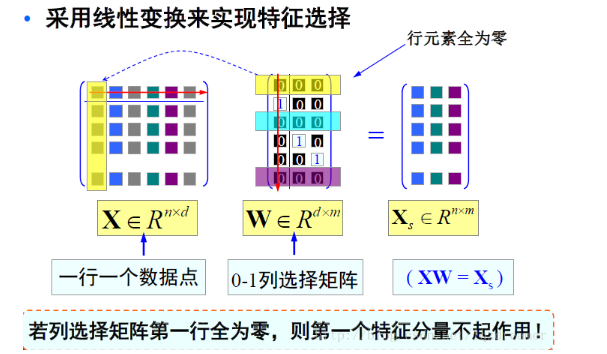
在特征选择中，通过稀疏化的特征选择矩阵来选取特征，即相当于是一种线性变换。
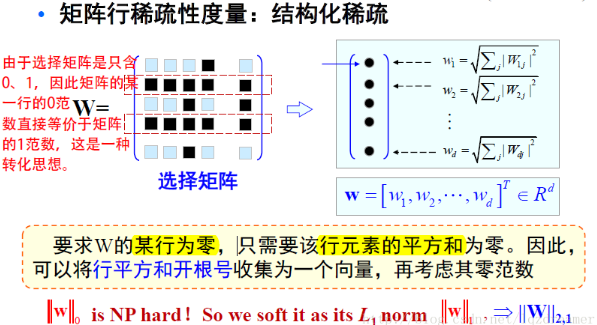
对于特征选择矩阵W，每一行（即行向量）用向量的2-范数描述，即
。那么，描述化之后即为向量
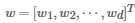，那么对整个选择矩阵W还需要用范数对
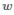进行描述，因为损失函数中的正则项，或称为正则化的项是一个数，而不是一个向量。因此再用1-范数对
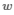描述，即是W的L2,1范数。
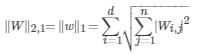
这便是矩阵的L2,1范数的实际描述过程。矩阵的L2,1范数满足矩阵范数的自反性、非负性、对称性和三角不等式关系，是一个范数。
先看上面L21范数的定义，注意原始矩阵是d行n列的，根号下平方是对列求和，也就是说是在同一行中进行操作的，根号部分就相当于一个L2范数，由此可以看出L2,1范数实则为矩阵X每一行的L2范数之和。在矩阵稀疏表示模型中，把它作为正则化项有什么作用呢？前面说到它是每一行的L2范数之和，在最小化问题中，只有每一行的L2范数都最小总问题才最小。而每一个行范数取得最小的含义是，当行内尽可能多的元素为0时，约束才可能取得最小。行内出现尽可能多的0元素，尽可能稀疏，也称为行稀疏。综上可以这样解释，不同于L1范数（矩阵元素绝对值之和）的稀疏要求，l21范数还要求行稀疏！
那么，在线性学习模型，损失函数如：
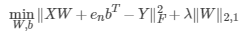
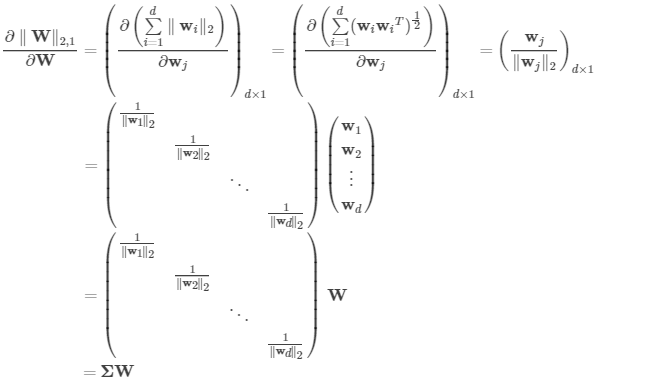
在优化中，矩阵的范数该如何求导？关于矩阵的F范数求导，可以参考矩阵的 Frobenius 范数及其求偏导法则（https://blog.csdn.net/txwh0820/article/details/46392293）。而矩阵L2,1范数求导如下推导：
对于一个矩阵W=[w1,⋯,wd]T , 其中wi 是W 的第i 行。由矩阵的定义有
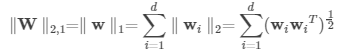
那么,L2,1范数的求导为：
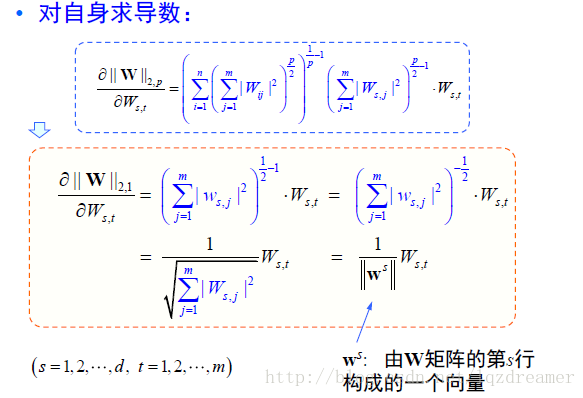
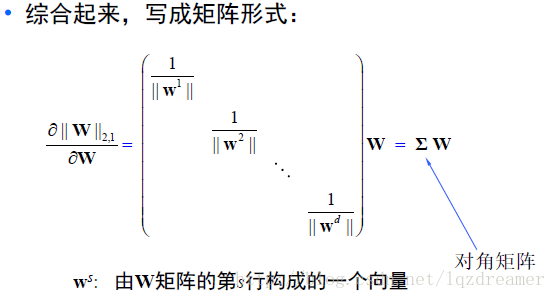
矩阵一般化L2,P范数的求导
就矩阵一般化L2,P范数给出推导：
矩阵的核范数Nuclear Norm
核范数||W||*是指矩阵奇异值的和，用于约束Low-Rank（低秩）。
从物理意义上讲，矩阵的秩度量的就是矩阵的行列之间的相关性。如果矩阵的各行或列是线性无关的，矩阵就是满秩的，也就是秩等于行数。秩可以度量相关性，而矩阵的相关性实际上有带有了矩阵的结构信息。如果矩阵之间各行的相关性很强，那么就表示这个矩阵实际可以投影到更低维的线性子空间，也就是用几个向量就可以完全表达了，它就是低秩的。所以：如果矩阵表达的是结构性信息，例如图像、用户-推荐表等，那么这个矩阵各行之间存在这一定的相关性，那这个矩阵一般就是低秩的。低秩矩阵每行或每列都可以用其他的行或列线性表出，可见它包含大量的冗余信息。利用这种冗余信息，可以对缺失数据进行恢复，也可以对数据进行特征提取。rank()是非凸的，在优化问题里面很难求解，rank(w)的凸近似就是核范数||W||*。
1）矩阵填充(Matrix Completion):
矩阵填充即矩阵补全，是低秩矩阵重构问题，例如推荐系统。其模型表述：已知数据是一个给定的m*n矩阵A，如果其中一些元素因为某种原因丢失了，能否根据其他行和列的元素，将这些元素恢复？当然，如果没有其他的参考条件，想要确定这些数据很困难。但如果已知A的秩rank(A)<<m且rank(A)<<n，那么可以通过矩阵各行(列)之间的线性相关将丢失的元素求出。这种假定“要恢复的矩阵是低秩的”是十分合理的，比如一个用户对某电影评分是其他用户对这部电影评分的线性组合。所以，通过低秩重构就可以预测用户对其未评价过的视频的喜好程度。从而对矩阵进行填充。
2）鲁棒主成分分析(Robust PCA)：
主成分分析，可以有效的找出数据中最“主要"的元素和结构，去除噪音和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。最简单的主成分分析方法就是PCA了。从线性代数的角度看，PCA的目标就是使用另一组基去重新描述得到的数据空间。希望在这组新的基下，能尽量揭示原有的数据间的关系。这个维度即最重要的“主元"。PCA的目标就是找到这样的“主元”，最大程度的去除冗余和噪音的干扰。
Robust PCA考虑的是这样一个问题：一般情况下数据矩阵X会包含结构信息，也包含噪声。那么可以将这个矩阵分解为两个矩阵相加，一个是低秩的（由于内部有一定的结构信息，造成各行或列间是线性相关的），另一个是稀疏的（由于含有噪声，而噪声是稀疏的），则Robust PCA可以写成优化问题：
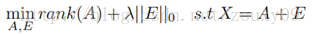
与经典PCA问题一样，Robust PCA本质上也是寻找数据在低维空间上的最佳投影问题。对于低秩数据观测矩阵X，假如X受到随机（稀疏）噪声的影响，则X的低秩性就会破坏，使X变成满秩的。所以就需要将X分解成包含其真实结构的低秩矩阵和稀疏噪声矩阵之和。找到了低秩矩阵，实际上就找到了数据的本质低维空间。PCA假设数据的噪声是高斯的，对于大的噪声或者严重的离群点，PCA会被它影响，导致无法正常工作。而Robust PCA则不存在这个假设，它只是假设噪声是稀疏的，而不管噪声的强弱如何。
由于rank和L0范数在优化上存在非凸和非光滑特性，所以一般将它转换成求解以下一个松弛的凸优化问题：
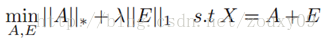
具体应用：考虑同一副人脸的多幅图像，如果将每一副人脸图像看成是一个行向量，并将这些向量组成一个矩阵的话，那么可以肯定，理论上，这个矩阵应当是低秩的。但是，由于在实际操作中，每幅图像会受到一定程度的影响，例如遮挡，噪声，光照变化，平移等。这些干扰因素的作用可以看做是一个噪声矩阵的作用。所以可以把同一个人脸的多个不同情况下的图片各自拉长一列，然后摆成一个矩阵，对这个矩阵进行低秩和稀疏的分解，就可以得到干净的人脸图像（低秩矩阵）和噪声的矩阵了（稀疏矩阵），例如光照，遮挡等等。
矩阵的迹范数Trace Norm
Schatten范数：
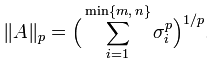
令p = 1 ，得到迹范数：
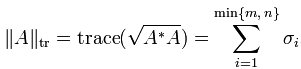
本文为自己学习过程中对其他资源的学习整理而得的学习笔记，内容源自：https://blog.csdn.net/lqzdreamer/article/details/79676305；https://blog.csdn.net/zchang81/article/details/70208061；https://blog.csdn.net/lj695242104/article/details/38801025
