1.2 磁盘存储链式结构B树与B+树

Linux C/C++服务器

多路查找树（B树、B+树）

我们前面讨论的红黑树，处理数据都是在内存中，因此考虑的都是内存中的运算时间复杂度。但若我们要操作的数据集非常大，大到内存已经没办法处理了怎么办呢？
这种情况下，对数据的处理需要不断从硬盘等存储设备中调入或调出内存页面，一旦涉及到这样的外部存储设备，关于时间复杂度的计算就会发生变化，访问元素的时间已经不仅仅是寻找该元素所需比较次数的函数，我们必须考虑对硬盘等外部存储设备的访问时间以及将会对该设备做出多少次单独访问。
试想一下，为了要在一个拥有几十万个文件的磁盘中查找一个文本文件，你设计的算法需要读取磁盘（磁盘寻址）上万次还是读取几十次，这是有本质差异的，此时为了降低对外存设备的访问次数，我们就需要新的数据结构来处理这样的问题，B树B+树（n叉树）
B树、B+树的本质是通过降低树的层高，减少对磁盘访问次数，来提升查询速度，查找复杂度\(log_{m}(n/m)\),m是叉的数量

B树与B+树区别与联系

1. B树所有节点即存储key也存储value，内存中存不下后存磁盘，名称为B-Tree，并没有B-树这种叫法
2. B+树只有在叶子节点存储数据value（叶子节点放在磁盘中），非叶子节点用来做索引key（非叶子结点在内存中），相比于B树，B+树更适合做磁盘索引，在大数据的存储和查找中使用较多，比如海量图像查找引擎
3. B树和B+树的结点添加、删除、查询基本相同

B树的定义

⼀种平衡的多路查找树，结点最⼤的孩⼦数⽬称为B树的阶，mysql、MongoDB等数据库的核心数据结构就是B+树

1. 每个结点至多拥有M棵子树；根结点至少拥有两棵子树，其余每个分支结点至少拥有M/2棵子树
2. 有K棵子树的分支结点存在k-1个关键字，关键字按照递增顺序进行排序，关键字数量满足ceil(M/2)-1 <= n <= M-1
3. 所有的叶结点都在同一层上

注意：我们说的6叉树是指，每个节点最多可拥有的子树个数，6叉树每个节点最多可拥有6颗子树，而每个节点中最多存储5个数据，如下图

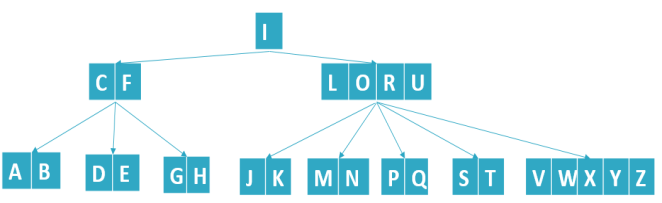
//6叉树的定义
#define SUB_M   3

struct _btree_node{
    /*
    int keys[2 * SUB_M-1];      //最多5个关键字
    struct _btree_node *childrens[2 * SUB_M];   //最多6颗子树    6叉树
    */

    int *keys;      //5
    struct _btree_node **childrens;   //6

    int num;    //实际存储的节点数量 <= M-1
    int leaf;   //是否为叶子节点
}

struct _btree {
    struct _btree_node *root;
}

B树添加结点

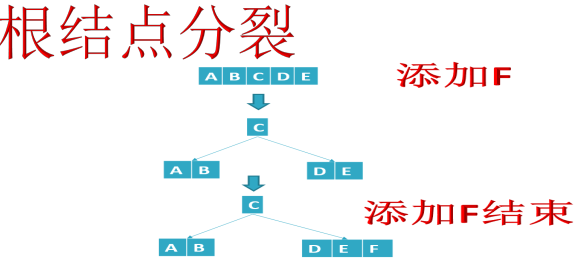
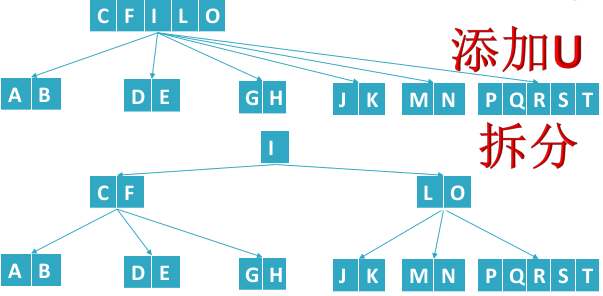
B树添加结点，只会添加在叶子结点上，重点是结点满了后，会发生分裂并向父结点上位。

• 添加的数据都是添加在叶子节点上，不会添加到根节点或中间节点
  
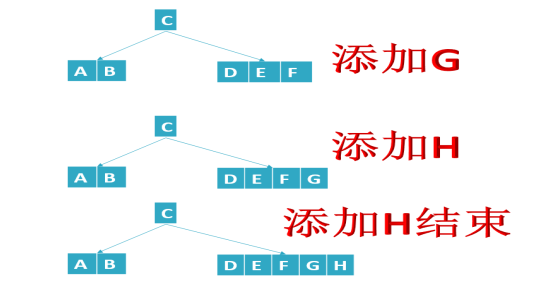
• 结点数据个数==M-1（结点满了的情况）,发生分裂（把(M-1)/2处数据放到父结点，其他数据分成两个结点）
  
  
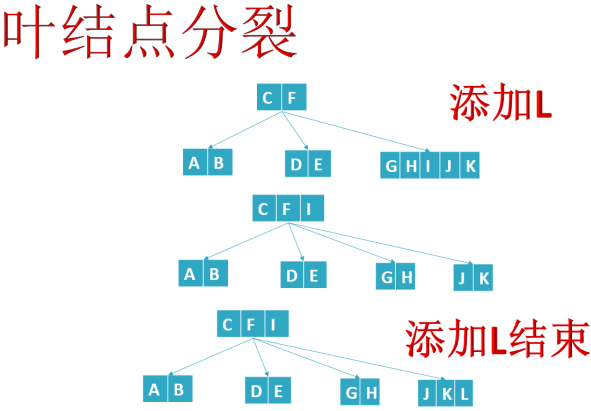
• 添加U，高度+1
  

---

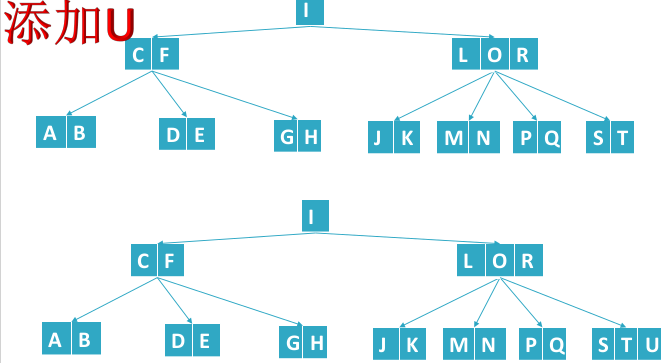
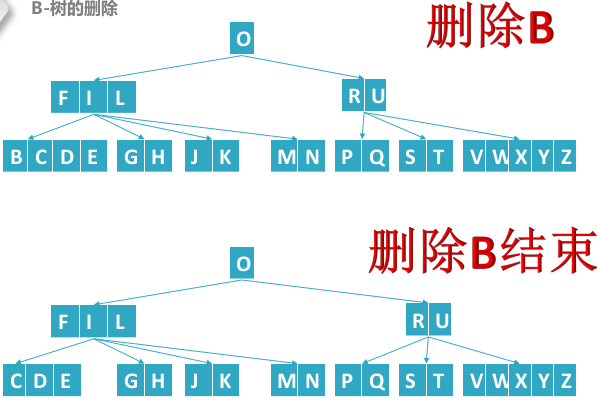
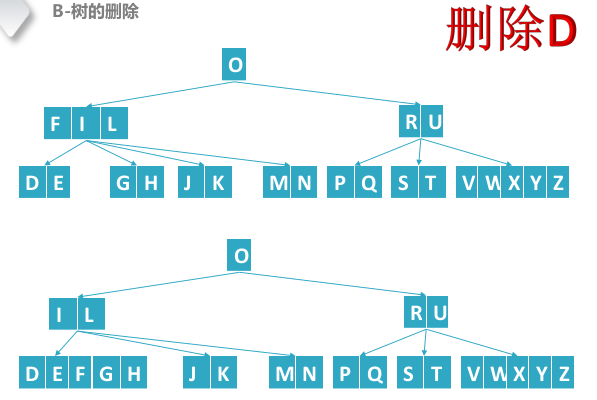
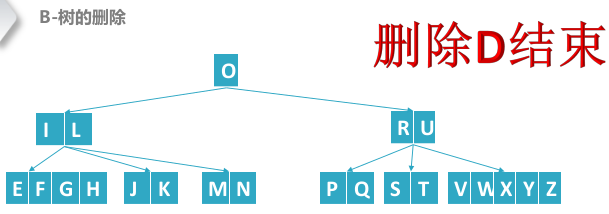
B树删除结点

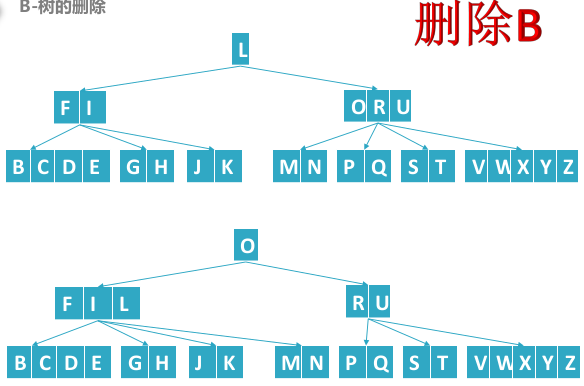
B树删除结点，删除叶子结点和中间结点类似，重点为向父结点借位再合并操作。

• 先合并或者借位转换成一个B树可以删除的状态，在进行删除
  

---

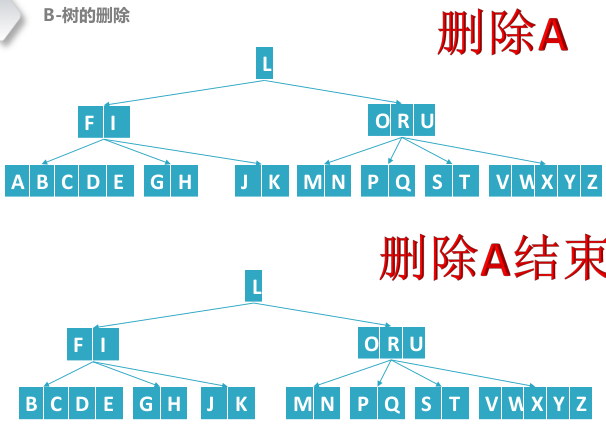
删除B结点，其中路径中间结点“FI”的关键字数量为(M-1)/2-1个，为了避免以后出现资源不足的现象，需要对"FI"先进行借位合并

---

B树添加及删除结点代码

/*用于结点分裂时创建新结点*/
btree_node *btree_create_node(int leaf){
    btree_node *node = (btree_node*)calloc(1, sizeof(btree_node));  //malloc需要手动清零，calloc会自动清零，set 0
    if(node == NULL) return NULL;   //在内存分配的时候一定要判断，当内存不够用的时候，malloc/calloc就会出错

    node->leaf = leaf;
    node->keys = calloc(2 * SUB_M -1, sizeof(int));
    node->childrens = (btree_node**)calloc(2 * SUB_M -1, sizeof(btree_node*));
    node->num = 0;

    return node;
}

/*删除结点*/
void btree_destory_node(btree_node *node){
    free(node->childrens);
    free(node->keys);
    free(node);
}

/*
非根结点分裂、上位：发生在B树添加元素的过程中,结点满了，需要先分裂再添加
btree *T：根节点
btree_node *x：被删除元素的父结点
int idx：位于父结点的第几颗子树
*/
void btree_split_child(btree *T, btree_node *x, int idx){
    btree_node *y = x->childrens[idx];    //满了的结点node_y
    btree_node *z = btree_create_node(y->leaf); //创建分裂后的新结点

    //z
    z->num = SUB_M - 1;

    int i=0;
    for(i=0; i < SUB_M-1; i++){
        z->keys[i] = y->keys[SUB_M+i];
    }
    if(y->leaf == 0){   //inner 是内结点，子树指针也要copy过去
        for(i=0; i < SUB_M-1; i++){
            z->childrens[i] = y->childrens[SUB_M+i];
        }
    }

    //y
    y->num = SUB_M;

    //中间元素上位
        //childrens 子树
    for(i=x->num; i >= idx+1; i--){             //寻找上为父结点的位置
        x->childrens[i+1] = x->childrens[i];    //父结点元素后移
    }
    x->childrens[i+1] = z;
        //key   
    for(i=x->num-1; i >= idx; i--){     //寻找上为父结点的位置
        x->keys[i+1] = x->keys[i];      //父结点后边元素后移 
    }
    x->keys[i] = y->keys[SUB_M];
    x->num += 1;
}

/*

*/
void btree_insert(btree *T, int key){
    btree_node *r = T->root;
    
    //根节点分裂（根节点满了）；创建一个空结点 指向root, 
    if(r->num == 2*SUB_M-1){
        btree_node *node = btree_create_node(0);
        T->root = node;
        node->childrens[0] = r;

        btree_split_child(T, node, 0);
    }
}


///b树 删除     


void btree_merge(btree *T, btree_node *x, int idx){

    btree_node *left = x->childrens[idx];
    btree_node *right = x->childrens[idx+1];

    left->keys[left->num] = x->keys[idx];

    int i=0;
    for(i=0; i<right->num; i++){
        left->keys[SUB_M+i] = right->keys[i];
    }
    if(!left->leaf){    //非叶子结点，要合并孩子结点指针
        for(i=0; i<SUB_M; i++){
            left->childrens[SUB_M+i] = right->childrens[i];
        }
    }
    left->num += SUB_M;

    btree_destory_node(right);

    //x key前移
    for(i=idx+1; i < x->num; i++){
        x->keys[i-1] = x->keys[i];
        x->childrens[i] = x->childrens[i+1];
    }
}

B+树完整代码