1.1 红黑树

Linux C/C++服务器

红黑树（rbTree）

一种特殊的平衡 二叉排序树，一般用于key,value查找，插入删除查找$O(log_{2}n)$,应用广泛；

定义

1. 具有二叉排序树性质
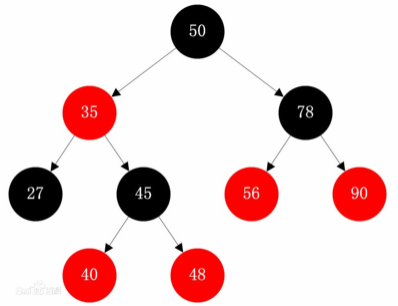
2. 每个结点是红的或者黑的，根结点是黑的，每个叶子结点是黑的(一般叶子结点都是隐藏的空结点)
3. 如果一个结点是红的，则它的两个儿子都是黑的
4. 对每个结点，从该结点到其子孙结点的所有路径上的包含相同数目的黑色结点
   

#define RED     0
#define BLACK   1
 
typedef int KEY_TYPE;
 
//这样写就把红黑树的性质单列出来了，_rbtree_node{if 0   else} 这一块方便写业务
#define RBTREE_ENTRY(name, type) \
    struct name {
        struct type *right;      \
        struct type *left;       \
        struct type *parent;     \
        unsigned char color;     \
    }
 
    
typedef struct _rbtree_node{   //这是红黑树中的一个节点node
    KEY_TYPE key;
    void *value;
 
#if 1
    struct _rbtree_node *right;
    struct _rbtree_node *left;
    struct _rbtree_node *parent;    //后续旋转操作时使用
    unsigned char color;
#else
    RBTREE_ENTRY(, rbtree_node) node;
#endif
 
} rbtree_node;
 
typedef struct _rbtree{          //这是一个红黑树的指针
    struct rbtree_node *root;
    struct rbtree_node *nil;   //叶子节点统一指向的节点    
} rbtree;

红黑树的旋转

1. 和AVL树一样，红黑树的旋转，只出现在插入和删除结点数据的时候
2. 旋转的过程中不会修改结点的颜色，只会修改三对指针的值，比较好理解

//左旋 左旋右旋不需要改变颜色
void rbtree_left_rotate(rbtree *T, rbtree_node *x){
    rbtree_node *y=x->right;
 
    //左旋总共有三对指针需要修改，第一对
    x->right = y->left;
    if(y->left != T->nil){
        y->left->parent = x;
    }
 
    //第二对
    y->parent = x->parent;
    if(x->parent == T->nil){
        T->root = y;
    }else if(x == x->parent->left){
        x->parent->left = y;
    }else{
        x->parent->right = y;
    }
 
    //第三对
    y->left = x;
    x->parent = y;
}
 
 
//右旋，在左旋函数上 x改为y y改为x left改为right right改为left
void rbtree_left_rotate(rbtree *T, rbtree_node *y){
    rbtree_node *x = y->left;
 
    //左旋总共有三对指针需要修改，第一对
    y->left = x->right;
    if(x->right != T->nil){
        x->right->parent = y;
    }
 
    //第二对
    x->parent = y->parent;
    if(y->parent == T->nil){
        T->root = x;
    }else if(y == y->parent->right){
        y->parent->right = x;
    }else{
        y->parent->left = x;
    }
 
    //第三对
    x->left = y;
    y->parent = x;
}

红黑树的插入与调整

1. 红黑树在插入一个结点之前，它已经是一颗红黑树
2. 红黑树插入结点为红色，在整个插入过程中插入节点的颜色不会改变，始终为红色
3. 插入后打破红黑树平衡（红黑树的定义），会通过旋转和改变parent节点的颜色，重新恢复平衡

//调整插入后的红黑树，再插入过程中z的颜色始终为红色，会改变parent节点的颜色
void rbtree_insert_fixup(rbtree *T, rbtree_node *z){
    //z为RED，父节点不能为红色 
    while(z->parent->color == RED){
        if(z->parent == z->parent->parent->left){
            rbtree_node *y = z->parent->parent->right;
            if(y->color == RED){
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;
 
                z = z->parent->parent;    //回溯 一直到根节点
            } else { //y == BLACK
                if(z == z->parent->right){
                    z = z->parent;
                    rbtree_left_rotate(T, z);
                }
 
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                rbtree_right_rotate(T, z->parent->parent);
            }
        }
    }
}
 
//插入，插入z节点的颜色为红色，插入的过程中自始至终都为红色
void retree_insert(rbtree *T, rebtree_node *z){
    rbtree_node *y = T->nil;    //定义临时节点
    rbtree_node *x = T->root;
    
    while (x != T->nil){
        y = x;
        if(z->key < x->key){
            x=x->left;
        }else if(z->key > x->key){
            x=x->right;
        }else{
            //Exist 根据业务场景 做处理
            return;
        }
    }
 
    if(y == T->nil){
        T->root=z;
    }else{
        if(y->key > z->key){
            y->left = z;
        }else{
            y->right = z;
        }
    }
 
    z->parent=y;
    z->left=T->nil;
    z->right=T->nil;
    z->color=RED;   //插入新节点颜色为红色
    
    rbtree_insert_fixup(T, z);
}

红黑树完整代码