index 数据结构与算法
二叉排序树
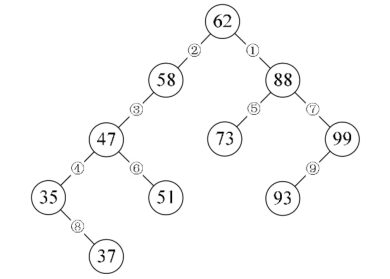
一颗二叉树,中序遍历有序,{35,37,47,51,58,62,73,88,93,99},我们通常称它为二叉排序树,又称为二叉查找树。
定义
- 若它的左子树不空,则左子树上所有节点的值均小于它的根结构的值;
- 若它的右子树不空,则右子树上所有节点的值均大于它的根结构的值;
- 它的左、右子树也分别为二叉排序树。
构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。
//二叉树的结构
typedef sturct BiTNode{
int data;
sturct BiTNode *lchild, *rchild;
}BiTNode,*BiTree;
查找
//递归查找二叉排序树T中是否存在Key,指针f指向T的双亲,其初始值为NULL;
//若查找成功,则指针p指向该数据元素结点,并放回true,否则指针p指向查找路径上访问的最后一个结点并返回false。
bool searchBST(BiTree T, int key, BiTree f, BiTree *p){
if(!T){
*p=f;
return false;
}
else if(key == T->data){
*P=T;
return true;
}
else if(key < T->data){
//在左子树继续查找
return searchBST(T->lchild, key, T, p);
}
else{
return searchBST(T->rchild, key, T, p);
}
}
插入
//二叉排序树T中的插入操作
bool insertBST(BiTree *T, int key){
BiTree p,s;
if(!searchBST(*T, key, NULL, &p)){
s=(BiTree)malloc(sizeof(BiNode));
s->data=key;
s->lchild = s->rchild=NULL;
if(!p)
*T=s;
else if(key < p->data)
p->lchild=s;
else
p->rchild=s;
return true;
}
else
return false;
}
删除
二叉排序树删除操作
被删除的结点存在以下三种情况:
- 叶子结点:直接删除即可
- 仅有左或右子树的结点:也不复杂
- 左右子树都有节点:
//二叉树删除代码
bool deleteBST(BiTree *T, int key){
if(!*T)
return false;
else{
if(key == (*T)->data)
return delete(T); //和searchBST唯一的区别
else if(key < (*T)->data)
return deleteBST(&(*T)->lchild, key);
else
return deleteBST(&(*T)->rchild, key);
}
}
//重点:从二叉排序树中删除节点p,并重接它的左或右子树。
bool delete(BiTree *p){
BiTree q,s;
if(*p->rchild == NULL){ //右子树空则只需重接它的左子树
q=*p;
*p=(*p)->lchild;
free(q);
}
esle if(*p->lchild == NULL){ //左子树空则只需重接它的右子树
q=*p;
*p=(*p)->rchild;
free(q);
}
else{ ///////////左右子树均不为空//////////
q=*p;s=(*p)->lchild;
while(s->rchild){ //转左,然后向右到尽头(找到待删结点的前驱)
q=s; s=s->rchild;
}
(*p)->data=s->data; //s指向被删结点的直接前驱
if(q!=*p)
q->rchild=s->lchild; //重接q的右子树
else
q->lchild=s->lchild; //重接q的左子树
free(s);
}
return true;
}
优缺点
- 二叉排序树是以链接的方式存储,保持了链接存储结构在执行插入和删除操作时不用移动元素的优点,只要找到合适的插入和删除位置后,仅需修改链接指针即可,插入删除的时间性能比较好。
- 二叉排序树的查找,走的就是从根节点到要查找的结点的路径,其比较次数等于给定值的结点在二叉排序树的层数。极端情况下,最少为1次,最多也不会超过树的深度。也就是说二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于,二叉排序树的形状是不确定的。
我们希望二叉排序树是比较平衡的,即其深度与完全二叉树相同,那么查找的时间复杂度也就为\(O(log_{2}n)\),近似于折半查找。
平衡二叉树(AVL树)
定义
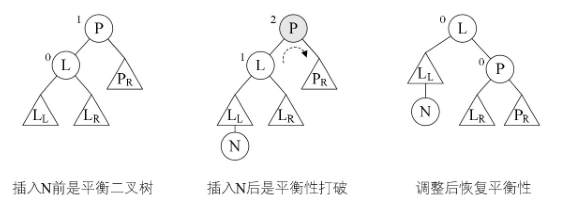
- 平衡二叉树,是一种二叉排序树,其中每一个节点的左子树和右子树的高度至多等于1。
- 当最小不平衡子树根结点的平衡因子BF大于1时,就右旋,小于-1时就左旋;
- 插入结点后,最小不平衡子树的BF与它的子树的BF符号相反时,就需要对结点先进性一次旋转以使符号相同后,再反向选转一次才能够完成平衡操作。
下面是代码部分,在二叉排序树结构上增加了一个bf,用来存储平衡因子。
typedef struct BiTNode{
int data;
int bf;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
左旋
#define LH +1 //左高
#define EH 0
#define RH -1
//对以指针T所指结点为根的二叉树作左平衡旋转处理,本算法结束时,指针T指向新的根节点
void LeftBalance(BiTree *T){
BiTree L,Lr;
L=(*T)->lchild; //L指向T的左子树根节点
switch(L->bf){ //检查T的左子树的平衡度,并作相应平衡处理
case LH: //新结点插入在T的左孩子的左子树上,要作单右旋处理
(*T)->bf=L->bf=EH;
R_Rotate(T);
break;
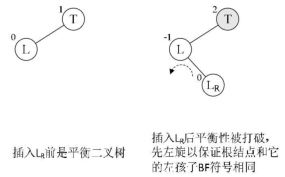
case RH: //新节点插入在T的左孩子的右子树上,要作双旋处理
Lr=L->rchild; //Lr指向T的左孩子的右子树跟
switch(Lr->bf){ //修改T及其左孩子的平衡因子
case LH: (*T)->bf=RH;
L->bf=EH;
break;
case EH: (*T)->bf=L->bf=EH;
break;
case RH: (*T)->bf=EH;
L->bf=LH;
break;
}
Lr->bf=EH;
L_Rotate(&(*T)->lchild); //对T的左子树作左旋平衡处理
R_Rotate(T); //对T作右旋平衡处理
}
}
//左旋
void R_Rotate(BiTree *P){
BiTree L;
L=(*P)->lchild; //L指向P的左子树根节点
(*P)->lchild=L->rchild; //L的右子树挂接为P的左子树
L->rchild=(*P);
*P=L; //P指向新的根节点
}
//左旋
void L_Rotate(BiTree *P){
BiTree R;
R=(*P)->rchild;
(*P)->rchild=R->lchild;
R->lchild=(*P);
*P=R;
}
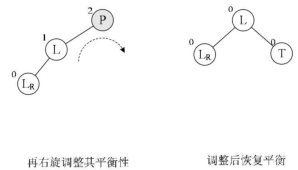
右平衡旋转和左平衡旋转代码非常类似,故将其省略
插入
有了这些准备,我们的主函数才算是正式登场了。
bool insertAVL(BiTree *T, int e, bool *taller){
if(!*T){ //根节点是否为空
*T=(BiTree)malloc(sizeof(BiTNode));
(*T)->data=e;
(*T)->lchild=(*T)->rchild=NULL;
(*T)->bf=EH;
*taller=true;
}
else{
if(e == (*T)->data){
*taller=false;
return false;
}
if(e < (*T)->data){
if(!insertAVL(&(*T)->lchild, e, taller)) //应继续在T的左子树中进行搜索,未插入
return false;
if(*taller){ //已插入到T的左子树中且左子树“长高”
switch((*T)->bf){
case LH: //原本左子树比右子树高,需要左平衡处理
LeftBalance(T);
*taller=false;
break;
case EH: //原本左右子树等高,现因左子树增高而树增高
(*T)->bf=LH;
*taller=true;
break;
case RH: //原本右子树比左子树高,现左右子树等高
(*T)->bf=EH;
*taller=false;
break;
}
}
}
else{
if(!insertAVL(&(*T)->rchild, e, taller))
return false;
if(*taller){
switch((*T)->bf){
case LH:
(*T)->bf=EH;
*taller=false;
break;
case EH:
(*T)->bf=RH;
*taller=true;
break;
case RH:
RightBalance(T);
*taller=false;
break;
}
}
}
}
return true;
}
优点
- 增删改查时间复杂度为 \(O(log_{2}n)\)
- 平衡的目的是增删改后,保证下次搜索能稳定排除一半的数据;
\(O(log_{2}n)\)的直观理解:100万个节点,最多比较20次;10亿个节点,最多比较30次;
红黑树
对每个结点,从该结点到其子孙结点的所有路径上的包含相同数目的黑色结点;内存中的数据查找一般都用红黑树
B、B+树
低层高的有序多叉树,磁盘中海量数据寻址一般都用B+树