index 数据结构与算法
图
图数据结构是比较重要、常用、复杂的结构,经常用于解决最优路径的问题。许多机器学习的算法如马尔可夫链、Apriori关联分析结构及算法与图有很多相似之处。
在线性表中,数据元素之间是被串起来的,仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继。在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关。图是一种较线性表和树更加复杂的数据结构。在图结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。最小生成树及最短路径会涉及动态规划的相关内容。
图的定义
图(Graph)是由顶点的有穷非空集合和顶点之间的连通关系集合组成,通常表示为:\(G(V,E)\),其中,\(G\)表示一个图,\(V\)是图\(G\)中顶点的集合,\(E\)是图中边的集合,可以是双向的也可以是单向的。
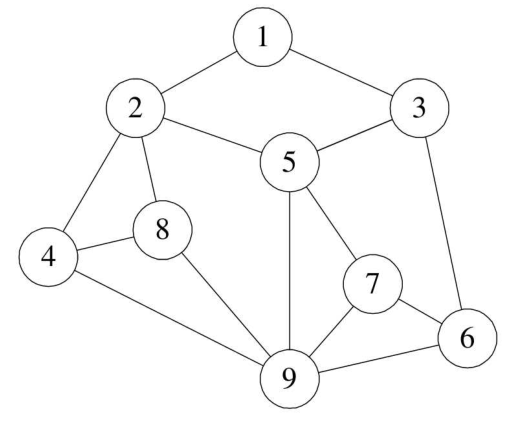
- 线性表中我们把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,我们则称之为顶点(Vertex)。
- 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图中,任意两个顶点之间都有可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
- 图按照有无方向分为无向图和有向图。无向图由顶点和边构成,有向图由顶点和弧构成。
图的存储表示方法
邻接矩阵
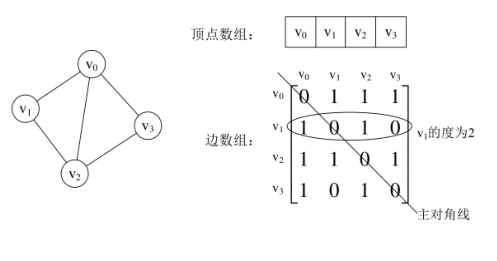
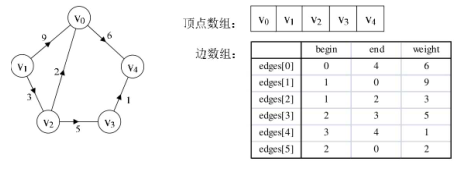
图是由顶点和边两部分组成,合在一起比较困难,那就很自然的考虑到分两个结构分别存储。顶点不分大小、主次,所以用一个一维数组存储。而边由于是顶点与顶点之间的关系,一维搞不定,那就考虑用一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
无向图:斜对角线为0,沿斜对角线对称。
有向图:斜对角线为0,沿斜对角线不对称。
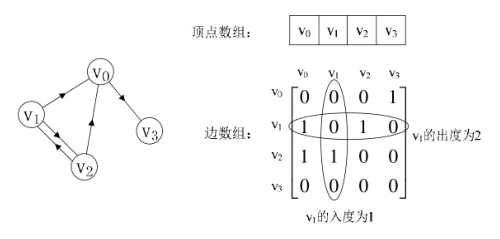
顶点数组为vertex[4]={v0,v1,v2,v3},边(弧)数组arc[4][4],这样我们就能轻松的给出图的数值存储结构啦。
邻接表
邻接矩阵这种结构用于表示稀疏有向图时,存在对存储空间的极大浪费:
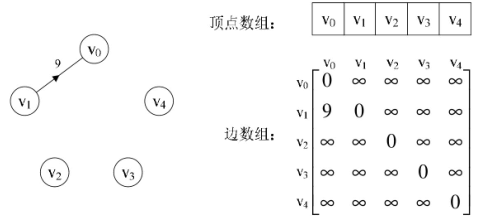
我们可以考虑对边或弧使用链式存储的方式来避免空间的浪费:
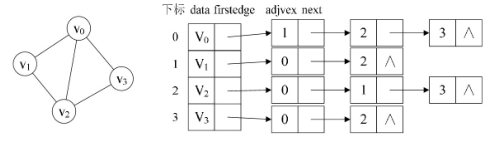
顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
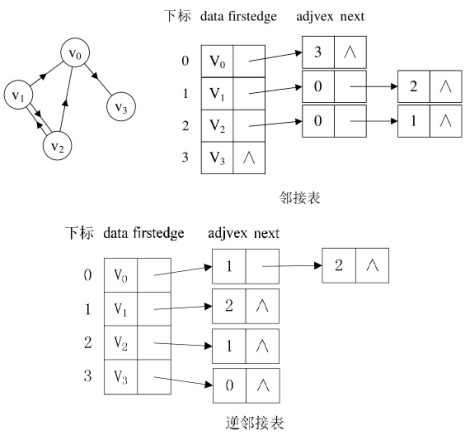
如果我们想知道某个顶点的“度”,就去查找这个顶点的边表中结点的个数;若是有向图,这样很容易得到每个顶点的“出度”。但也有时为了便于确定顶点的入度或以顶点为弧头的弧,我们可以建立一个有向图的逆邻接表,这样对于有向图的入度和出度都很容易查询了:
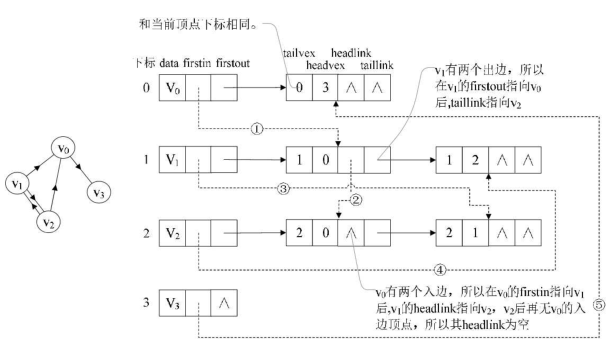
十字链表
十字链表是邻接表与逆邻接表的组合
重新定义后的顶点表结构:
重新定义后的边表结构:

包含邻接表和逆邻接表的十字链表:
边集数组
图的遍历
深度优先遍历
dfs本质上就是递归,栈stack先进后出思想
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
int numIslands(vector<char>& grid){
int numlands=0;
for(int i=0; i<grid.size();i++){
for(int j=0; j<grid[0].size(); j++){
if(grid[i][j]=='1'){
numlands++;
dfs(grid,i,j);
}
}
}
}
void dfs(vector<char>& grid, int i, int j){
grid[i][j]='0'; //沉没此块陆地
if(i-1>=0 && grid[i-1][j]=='1') dfs(grid, i-1, j);
if(i+1<grid.size() && grid[i+1][j]=='1') dfs(grid, i+1, j);
if(j-1>=0 && gri
d[i][j-1]=='1') dfs(grid, i, j-1);
if(j+1<grid.size() && grid[i][j+1]) dfs(grid, i, j+1);
}
广度优先遍历
会用到队列的思想queue先进先出
int numIslands(vector<vector<char>>& grid) {
int nr = grid.size();
if (!nr) return 0;
int nc = grid[0].size();
int num_islands = 0;
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
++num_islands;
grid[r][c] = '0';
queue<pair<int, int>> neighbors;
neighbors.push({r, c});
while (!neighbors.empty()) {
auto rc = neighbors.front();
neighbors.pop();
int row = rc.first, col = rc.second;
if (row - 1 >= 0 && grid[row-1][col] == '1') {
neighbors.push({row-1, col});
grid[row-1][col] = '0';
}
if (row + 1 < nr && grid[row+1][col] == '1') {
neighbors.push({row+1, col});
grid[row+1][col] = '0';
}
if (col - 1 >= 0 && grid[row][col-1] == '1') {
neighbors.push({row, col-1});
grid[row][col-1] = '0';
}
if (col + 1 < nc && grid[row][col+1] == '1') {
neighbors.push({row, col+1});
grid[row][col+1] = '0';
}
}
}
}
}
return num_islands;
}
最小生成树
用于解决将图中所有节点连接起来的最小成本的问题
如何构建最小生成树?
普里姆(Prim)算法
普里姆(Prim)算法是以某顶点为起点,逐步找各顶点上最小权值的边来构建最小生成树的。
- 已选定点集合,未选顶点集合,连接区域
- 每次从连接区域中选择最小边,更新已选顶点集合和未选顶点集合
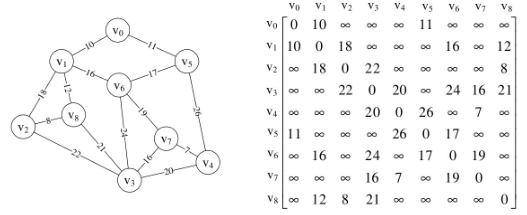
void MiniSpanTree_Prim(MGraph G){
int min,i,j,k;
int adjvex[MAXVEX]; //存放顶点下标,MAXVEX=9,顶点个数为9
int lowcost[MAXVEX]; //存放边的权值
lowcost[0] = 0; //我们从顶点v0开始,事实上最小生成树从哪个顶点开始计算都无所谓,我们假定从v0开始,之后凡是lowcost数组中的值被设置为0就是表示下标的顶点被纳入最小生成树
adjvex[0] = 0;
for(i=1; i<G.numVertexes; i++){
lowcost[i]=G.arc[0][i]; //将v0顶点与之有边的权值存入数组
adjvex[i] = 0; //初始化都为v0的下标
}
for(i=1; i<G.numVertexes; i++){
//初始化最小权值,通常设置为不可能的大数字如32767、65535等
min=INFINITY;
j=1; k=0;
while(j<G.numVertexes){
if(lowcost[j] != 0 && lowcost[j]<min){
min=lowcost[j];
k=j;
}
j++;
}
printf("(%d, %d)", adjvex[k], k);
lowcost[k]=0; //加入最小生成树,原始边改为0,方便之后判断
for(j=1; j<G.numVertexes; j++){
//若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值
if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j]){
lowcost[j] = G.arc[k][j]; //将较小权值存入lowcost
adjvex[j] = k; //将下标为k的顶点存入adjvex
}
}
}
}
克鲁斯卡尔(Kruskal)算法
对边集数组中的边进行排序,按从小到大的顺序选边,通过判断是否生成环路来选择最小生成树的顶点
- 将图中所有的边全部取出,并进行从小到大的排序
- 每次按从小到次序取出一条边进行回填,如果没有构成环则回填成功
- 当包含所有顶点后停止回填并返回
//边集数组的结构定义
typedef struct{
int begin;
int end;
int weight;
} Edge;
void MiniSpanTree_Kruskal(MGraph G){
int i,n,m;
Edge edges[MAXEDGE]; //边集数组
int parent[MAXVEX]; //用来判断边与边是否形成环路
for(int i=0; i<G.numEdges; i++) //G为升序边集数组
parent[i]=0;
for(i=0; i<G.numEdges; i++){
n=Find(parent, edges[i].begin);
m=Find(parent, edged[i].end);
if(n != m){
parent[n]=m; //加入最小生成树的标志
printf("(%d, %d) %d", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
int Find(int *parent, int f){
while(parent[f] > 0)
f=parent[f];
return f;
}
最短路径
Dijkstra 迪杰斯特拉算法
个人感觉思路和Prim算法有点像,结构是用的无向图中的邻接矩阵
#define MAXVEX 9
#define INFINITY 65535
typedef int Patharc[MAXVEX]; //用于存储最短路径下标的数组
typedef int ShortPathTable[MAXVEX]; //用于存储到各点最短路径的权值和
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D){
int v,w,k,min;
int final[MAXVEX];
for(v=0; v<G.numVertexes; v++){
final[v]=0;
(*D)[v]=G.arc[v0][v];
(*P)[v]=-1;
}
(*D)[v0]=0;
final[v0]=1;
for(v=1; v<G.numVertexes; v++){
min=INFINITY;
for(w=0; w<G.numVertexes; w++){
if(!final[w] && (*D)[w]<min){
k=w;
min=(*D)[w];
}
}
final[k]=1;
for(w=0; w<G.numVertexes; w++){
if(!final[w] && (min + G.arc[k][w] < (*D)[w])){
(*D)[w]=min+G.arc[k][w];
(*P)[w]=k;
}
}
}
}
Floyd 弗洛伊德算法
“有向图“中的最短路径问题,实际可应用场景很多,以后有时间再更



