Index LeetCode
动态规划和其它遍历算法(如深/广度优先搜索)都是将原问题拆成多个子问题然后求解,他们之间的最本质区别是,动态规划保存子问题的解,避免重复计算。
解决动态规划问题的关键是找到状态转移方程,这样我们可以通过计算和存储子问题的解来求解最终问题。
状态转移矩阵及dp数组初始化
BM62.斐波那契数列(509.斐波那契数列)[easy]
输入:n=4
输出:3
说明:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
int fib(int n){
if(n<=1) return n;
int res=0, a=0, b=1;
for(int i=2; i<=n; i++){
res=a+b;
a=b;
b=res;
}
return res;
}
BM63.跳台阶(剑指Offer10-II.青蛙跳台阶)[easy]
输入:n=2,n=7,n=0
输出:2,21,1
说明:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
int numWays(int n){
if(n==0 || n==1) return 1;
int res=0, a=1, b=1;
for(int i=2; i<=n; i++){
res=(a+b)%1000000007;
a=b;
b=res;
}
return res;
}
BM64.最小花费爬楼梯(746.使用最小花费爬楼梯)[easy]
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
dp[i]=min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
int minCostClimbingStairs(vector<int>& cost){
vector<int> dp(cost.size()+1, 0); //dp[i]表示爬到第i阶楼梯需要的最小花费
for(int i=2; i<=cost.size(); i++){
dp[i]=min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]); //每次选最小的方案
}
return dp[cost.size()];
}
BM65.最长公共子序列II(1143.最长公共子序列)[medium]
输入:text1 = "abcde", text2 = "ace"
输出:3
说明:给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
动态规划
int longestCommonSubsequence(string text1, string text2){
vector<vector<int>> dp(text1.size()+1, vector<int>(text2.size()+1, 0));
for(int i=1; i<=text1.size(); i++){
for(int j=1; j<=text2.size(); j++){
if(text1[i-1] == text2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i-1][j], dp[i][j-1]);
}
}
}
return dp[text1.size()][text2.size()];
}
BM66.最长公共子串(1143.最长公共子序列)[medium]
输入:"1AB2345CD","12345EF"
输出:"2345"
说明:给定两个字符串str1和str2,输出两个字符串的最长公共子串
题目保证str1和str2的最长公共子串存在且唯一。
string LCS(string str1, string str2){
vector<vector<int>> dp(str1.size()+1, vector<int>(str2.size()+1, 0));
int max=0, pos=0;
for(int i=1; i<=str1.size(); i++){
for(int j=1; j<=str2.size(); j++){
if(str1[i-1] == str2[j-1]){ //两字符相等
dp[i][j]=dp[i-1][j-1]+1; //长度增加
}else{ //否则
dp[i][j]=0; //该位置为0
}
if(dp[i][j] > max){ //跟新最大长度与位置
max=dp[i][j];
pos=i-1;
}
}
}
return str1.substr(pos-max+1, max);
}
BM67.不同路径的数目I(62.机器人不同路径)[medium]
输入:m = 3, n = 7
输出:28
说明:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径?
int uniquePaths(int m, int n){
vectro<vector<int>> dp(m, vector<int>(n, 0));
for(int i=0; i<m; i++){
dp[i][0]=1; //只有一行时,只有一种路径
}
for(int i=0; i<n; i++){
dp[0][i]=1; //只有一列时,只有一种路径
}
for(int i=1; i<m; i++){
for(int j=1; j<n; j++){
dp[i][j]=dp[i-1][j]+dp[i][j-1]; //路径等于左方格子的路径数加上上方格子的路径数
}
}
return dp[m-1][n-1];
}
BM68.矩阵的最小路径和(64.最小路径和)[medium]
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
动态规划
int minPathSum(vector<vector<int>>& grid){
int m=grid.size(), n=grid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
dp[0][0]=grid[0][0];
for(int i=1; i<m; i++){
dp[i][0]=dp[i-1][0]+grid[i][0];
}
for(int i=1; i<n; i++){
dp[0][]=dp[0][i-1]+grid[0][i-1];
}
for(int i=1; i<m; i++){
for(int j=1; i<n; j++){
dp[i][j] = min(dp[i-1][j], dp[i][j-1])+grid[i][j];
}
}
return dp[m-1][n-1];
}
BM69.把数字翻译成字符串(剑指Offer46.把数字翻译成字符串)[medium]
输入:12258
输出:5
解释:12258有5种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
说明:给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
状态定义:设动态规划列表dp,dp[i]代表以 \(x_i\) 为结尾的数字的翻译方案数量。
转移方程:若 \(x_i\) 和 \(x_{i-1}\) 组成的两位数字可以被翻译,则dp[i]=dp[i-1]+dp[i-2];否则dp[i]=dp[i-1]。
可被翻译的两位数区间:当\(x_{i-1}\)=0时,组成的两位数是无法被翻译的(例如 00,01,02,...),因此区间为[10,25]。
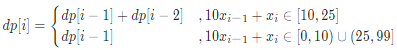
初始状态:dp[0]=dp[1]=1,即“无数字”和“第1位数字”的翻译方法数量均为1;
返回值:dp[n],即此数字的翻译方案数量。
Q:无数字情况dp[0]=1从何而来?
A:当num第1,2位的组成的数字在[10,25]时,显然应有2种翻译方法,即dp[2]=dp[1]+dp[0]=2,而显然dp[1]=1,因此推出dp[0]=1;
int translateNum(int num){
string src=to_string(num);
vector<int> dp(src.size()+1);
dp[0]=1;
dp[1]=1;
for(int i=2; i<=src.size(); i++){
int n=(src[i-2]-'0')*10 + (src[i-1]-'0');
if(n>=10 && n<=25){
dp[i]=dp[i-1]+dp[i-2];
}else{
dp[i]=dp[i-1];
}
}
return dp[src.size()];
}
BM70.兑换零钱I(322.零钱兑换)[medium]
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
说明:给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
动态规划,hard
int coinChange(vector<int>& coins, int amount){
int Max=amount+1;
vector<int> dp(amount+1, Max);
dp[0]=0;
for(int i=1; i<amount; i++){
for(int j=0; j<coins.size(); j++){
if(i>=coins[j]){
dp[i]=min(dp[i], dp[i-coins[j]]+1);
}
}
}
return dp[amount]>amount ? -1:dp[amount];
}
BM71.最长上升子序列I(300.最长递增子序列)[medium]
输入:nums=[10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4
动态规划
int lengthOfLIS(vector<int>& nums){
if(nums.size() <= 1) return nums.size();
vector<int> dp(nums.size(), 1); //设置数组长度大小的动态规划辅助数组
int res=0;
for(int i=1; i<nums.size(); i++){
for(int j=0; j<i; j++)
if(nums[i] > nums[j])
dp[i]=max(dp[i], dp[j]+1); //dp[i]与dp[j]+1,取最大的
res=max(res, dp[i]);
}
return res;
}
BM72.连续子数组的最大和(53.最大子序和)[medium]
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6
动态规划:dp[i]=max(dp[i-1]+nums[i], nums[i])、贪心:-
int maxSubArray(vector<int>& nums){
if(nums.size() == 0) return 0;
vector<int> dp(nums.size(), 0);
dp[0]=nums[0];
int res=dp[0];
for(int i=1; i<nums.size();i++){
dp[i]=max(dp[i-1]+nums[i], nums[i]); //状态转移公式
res=max(res, dp[i]);
}
return res;
}
BM73.最长回文子串(5.最长回文子串)[medium]
输入:给你一个字符串 s,找到 s 中最长的回文子串 s = "babad"
输出:"bab","aba" 同样是符合题意的答案。
中心扩散法,双指针
string longestPalindrome(string s){
int start=0, end=0;
for(int i=0; i<s.size(); i++){
auto[left1, right1]=cent_Expand(s, i, i); //奇数
auto[left2, right2]=cent_Expand(s, i, i+1); //偶数
if(right1-left1 > end-start){
start=left1; end=right1;
}
if(right2-left2 > end-start){
start=left2; end=right2;
}
}
return s.substr(start, end-start+1);
}
pair<int, int> cent_Expand(const string& s, int left, int right){
while(left>=0 && right<s.size() && s[left]==s[right]){
left--;
right++;
}
return {left+1, right-1};
}
BM75.编辑距离I(72.编辑距离)[hard]
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
dp[i][j]=min(dp[i][j], min(dp[i-1][j], dp[i][j-1]))+1
int minDistance(string word1, string word2){
int m=word1.size(), n=word2.size();
vector<vector<int>> dp[m+1, vector<int>(n+1, 0)];
//dp[i][j]表示到word[i]和word[j]为止的子串需要的编辑距离
for(int i=1; i<=m; i++) //初始化边界
dp[i][0]=dp[i-1][0]+1;
for(int i=1; i<=n; i++)
dp[0][i]=dp[0][i-1]+1;
for(int i=1; i<=m; i++)
for(int j=1; j<=n; j++){
if(word1[i-1] == word2[j-1]) //若是字符相同,此处不用编辑
dp[i][j]=dp[i-1][j-1];
else
dp[i][j]=min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]))+1; //选取最小距离加上此处编辑距离1
}
return dp[m][n];
}
BM76.正则表达式匹配(10.正则表达式匹配)[hard]
输入:s = "aa", p = "a";s = "aa", p = "a";s = "ab", p = "."
输出:false; true; true
说明:给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '' 的正则表达式匹配。'.' 匹配任意单个字符,'' 匹配零个或多个前面的那一个元素
bool isMatch(string s, string p){
int n1=s.size(), n2=p.size();
//dp[i][j]表示到s前i个字符和p前j个字符是否匹配
vector<vector<bool>> dp(n1+1, vector<bool>(n2+1, false));
dp[0][0]=true; //两个都为空串自然匹配
for(int i=2; i<=n2; i++){ //初始化str为空的情况,字符串下标从1开始
if(p[i-1]=='*') //匹配零个或多个前面的那一个元素
dp[0][i]=dp[0][i-2]; //与再前一个能够匹配空串有关
}
for(int i=1; i<=n1; i++){ //遍历s每个长度
for(int j=1; j<=n2; j++){ //遍历p每个长度
//当前字符不为*,用.去匹配或字符直接相同
if(p[j-1] != '*' && (p[j-1] == '.' || p[j-1]==s[i-1])){
dp[i][j]=dp[i-1][j-1];
}else if(j>=2 && p[j-1]=='*'){ //当前的字符为*
//若是前一位为.或者前一位可以与这个数字匹配
if(p[j-2]=='.' || p[j-2]==s[i-1])
dp[i][j]=dp[i-1][j] || dp[i][j-2];
else
dp[i][j]=dp[i][j-2]; //不匹配
}
}
}
return dp[n1][n2];
}
BM77.最长括号子串(32.最长有效括号)[hard]
输入:s = "(()";s=")()())"
输出:2; 4
栈
int longestVaildParentheses(string s){
int maxans = 0;
stack<int> stk;
stk.push(-1);
for(int i=0; i<s.length(); i++){
if(s[i] == '('){
stk.push(i);
}else{
stk.pop();
if(stk.empty()){
stk.push(i);
}else{
maxans=max(maxans, i-stk.top());
}
}
}
return maxans;
}
BM78.打家劫舍I(198.打家劫舍)[medium]
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4
说明:如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
动态规划:初始化,dp[0]=nums[0];状态转移,dp[i]=max(dp[i-1], nums[i]+dp[i-2])
int rob(vector<int>& nums){
if(nums.size()==1) return nums[0];
vector<int> dp(nums.size(), 0); //dp[i-1]表示长度为i的数组,最多能偷取多少钱
dp[0]=nums[0]; //长度为1只能偷第一家
dp[1]=max(nums[0], nums[1]);
for(int i=2; i< nums.size(); i++){
dp[i]=max(dp[i-1], nums[i]+dp[i-2]);
}
return dp[nums.size()-1];
}
BM79.打家劫舍II(213.打家劫舍II)[medium]
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的
说明:213与198区别在于 213数组头和尾认为是相邻的,也就是说头和尾最多只能偷一家,分成两个数组分别计算,[0,n-2],[1,n-1]取最大的
int rob(vector<int>& nums){
int head=0 ,tail=0, n=nums.size();
if(n==1) return nums[0];
if(n==2) return max(nums[0], nums[1]);
vector<int> dp(n, 0);
//[0,n-2] 下标区间
dp[0]=nums[0];
dp[1]=max(nums[0], nums[1]);
for(int i=2; i<n-1; i++){
dp[i]=max(dp[i-1], nums[i]+dp[i-2]);
}
head=dp[n-2];
//[1, n-1] 下标区间
dp[1]=nums[1];
dp[2]=max(nums[1], nums[2]);
for(int i=3; i<n; i++){
dp[i]=max(dp[i-1], nums[i]+dp[i-2]);
}
tail=dp[n-1];
return max(head, tail);
}
BM80.买卖股票的最好时机I(121.买卖股票的最佳时机)[easy]
输入:[7,1,5,3,6,4]
输出:5
解释:股票只能买卖一次。在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
暴力、贪心、动规
//暴力--超时
int maxProfit(vector<int>& prices){
int res=0;
for(int i=0; i<prices.size(); i++){
for(int j=0; j<i; i++){
res=max(res, prices[i]-prices[j]);
}
}
return res;
}
//贪心:股票只能买卖一次,取左边最小,右边最大的即可
int maxProfit(vector<int>& prices){
int low=INT_MAX;
int res=0;
for(int i=0; i<prices.size(); i++){
low=min(low, prices[i]); //去左边最小
res=max(res, prices[i]-low); //直接取最大区间利润
}
return res;
}
//动态规划
int maxProfit(vector<int>& prices){
int n=prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0)); //dp[i][0]表示某一天不持股到该天为止的最大收益,dp[i][1]表示某天持股,到该天位置的最大收益
dp[0][0]=0; //第一天不持股,总收益为0
dp[0][1]=-prices[0]; //第一天持股,总收益减去该天的股价
for(int i=1; i<n; i++){ //遍历后续每天,状态转移
dp[i][0]=max(dp[i-1][0], dp[i-1][1]+prices[i]);
dp[i][1]=max(dp[i-1][1], -prices[i]);
}
return dp[n-1][0]; //最后一天不持股,到今天为止的最大收益
}
BM81.买卖股票的最好时机II(122.买卖股票的最佳时机II)[medium]
输入:prices = [7,1,5,3,6,4]
输出:7
解释:可以多次买入卖出。在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。 总利润为 4 + 3 = 7 。
动态规划:
int maxProfit(vector<int>& prices){
int res=0;
int n=prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0)); //dp[i][0]表示某一天不持股到该天为止的最大收益,dp[i][1]表示某天持股,到该天为止的最大收益
dp[0][0]=0; //第一天不持股,总收益为0
dp[0][1]=-prices[0]; //第一天持股,总收益为减去该天的股价
for(int i=1; i<n; i++){ //遍历后续每天,状态转移
dp[i][0]=max(dp[i-1][0], dp[i-1][1]+prices[i]);
dp[i][1]=max(dp[i-1][1], dp[i-1][0]-prices[i]);
}
return dp[n-1][0];
}
BM82.买卖股票的最好时机III(123.买卖股票的最佳时机III)[hard]
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:你最多可以完成两笔交易。在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
动态规划
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int> > dp(n, vector<int>(5, -10000)); //初始化dp为最小
dp[0][0] = 0; //第0天不持有股票
dp[0][1] = -prices[0]; //第0天持有股票
for(int i = 1; i < n; i++){ //状态转移
dp[i][0] = dp[i - 1][0]; //表示第i天为止没有买过股票的最大收益
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]); //表示第i天为止没有买过一次股票,没有卖出的最大收益
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]); //表示第i天为止有买一次股票,也卖出过一次的最大收益
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]); //表示第i天为止买两次股票,只卖出过一次的最大收益
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]); ////表示第i天为止没有买两次次股票,也卖出过两次的最大收益
}
return max(dp[n - 1][2], max(0, dp[n - 1][4]));
}


