《神经网络与深度学习-邱锡鹏》读书笔记
神经元
神经元是构成神经网络的基本单元,神经元的结构如下图所示:
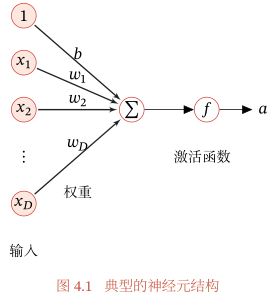
假设一个神经元接收D个输入$x_1,x_2,...x_D$,令向量$x=[x_1;x_2;...;x_D]$来表示这组输入,并用净输入$z$表示一个神经元所获得的输入信号$x$的加权和,
$z={\sum}_{d=1}^{D} w_d x_d+b = w^Tx+b$
其中,$w=[w_1;w_2;...;w_D]$是D维的权重向量,b是偏置。
净输入$z$在经过一个非线性函数$f(·)$后,得到神经元的活性值$a$,
$a=f(z)$,
其中非线性函数$f(·)$称为激活函数(Activation Function).
激活函数
激活函数:激活函数在神经元中非常重要,为了增强网络的表示能力和学习能力,激活函数需要具备以下几点性质
- 连续并可导(允许少数点上不可导)的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数
- 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率
- 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性
常用的激活函数
种类:
- Sigmoid型函数:Logistic、Tanh
- ReLU(Rectified Linear Unit,修正线性单元)函数
- Swish函数(是一种自门控(Self-Gated)激活函数)
- GELU(Gaussian Error Linear Unit,高斯误差线性单元)
- Maxout单元(一种分段线性函数)
详细介绍:
Sigmoid型函数
1.1 Logistic激活函数
函数定义为 ${\sigma}(x)=\frac{1}{1+exp(-x)}$ exp,高等数学里以自然常数e为底的指数函数,exp(-x)即 $e^{-x}$
1.2 Tanh激活函数
函数定义为 $tanh(x)=\frac{exp(x)-exp(-x)}{exp(x)+exp(-x)}$

1.3 Hard-Logistic函数和Hard-Tanh函数
Logistic函数和Tanh函数都是Sigmoid型函数,具有饱和性,但是计算开销较大。
Logistic函数在0附近的一阶泰勒展开为 $g_l(x){\approx}{\sigma}(0)+x*{\sigma}'(0) = 0.25x+0.5$
这样Logistic函数可以用分段函数hard-logistic(x)来近似
\begin{equation}
hard-logistic(x)=\left \{
\begin{array}{ll}
1 & g_l(x) \ge 1 \\
g_l & 0<g_l(x)<1 \\
0 & g_l(x) \le 0
\end{array} \right. \\
= max(min(g_l(x),1),0) \\
= max(min(0.25x+0.5,1),0)
\end{equation}
同样,Tanh函数在0附近的一阶泰勒展开为 $g_l(x)\approx tanh(0)+x*tanh'(0)=x$
$hard-tanh(x)=max(min(g_t(x),1),-1)=max(min(x,1),-1)$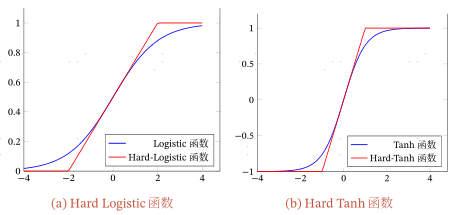
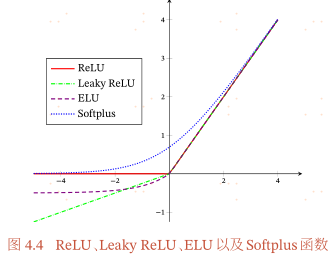
ReLU函数
1.1 ReLU函数
ReLU(Rectified Linear Unit,修正线性单元),也叫Rectifier函数,是目前深度网络中经常使用的激活函数,ReLU实际上是一个斜坡(ramp)函数,定义为
\begin{equation}
ReLU(x)= \left \{
\begin{array}{ll}
x & x \ge 0 \\
0 & x<0
\end{array} \right. \\
=max(0,x)
\end{equation}
优点:采用ReLU的神经元只需要进行加、乘和比较的操作,计算上更加高效,ReLU函数也被认为具有生物学合理性,比如单侧抑制、宽兴奋边界(即兴奋程度可以非常高),Sigmoid型激活函数会导致一个非稀疏的神经网络,而ReLU却具有很好的稀疏性,大约50%的神经元会处于激活状态;在优化方面,相比于Sigmoid型函数的两端饱和,ReLU函数为左饱和函数,且在x>0时导数为1,在一定程度上缓解了神经网络的梯度消失问题,加速梯度下降的收敛速度。
缺点:ReLU函数的输出是非零中心化的,给后一层的神经网络引入偏执偏移,会影响梯度下降的效率。此外ReLU神经元在训练时比较容易“死亡”,在训练时,如果参数在一次不恰当的更新后,第一个隐藏层中的某个ReLU神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活。这种现象称为死亡ReLU问题,并且也有可能发生在其他隐藏层。
在实际使用中,为了避免上述情况,有几种ReLU的变种也会被广泛使用。
1.2 带泄露、参数的ReLU
带泄露的ReLU(Leaky ReLU)在输入x<0时,保持一个很小的梯度$ \gamma $,这样当神经元非激活时也能有一个非零的梯度可以更新参数,避免永远不能被激活,带泄露的ReLU的定义如下:
\begin{equation}
LeakyReLU(x) = \left\{
\begin{array}{ll}
x & \text{if x > 0} \\
\gamma x & \text{if x $\le$ 0}
\end{array} \right. \\
=max(0,x) + \gamma min(0,x).
\end{equation}
其中$\gamma$是一个很小的常熟,比如0.01.当$\gamma$<1时,带泄露的ReLU也可以写为:LeakyReLU(x)=max(x,$\gamma x$),相当于是一个比较简单的maxout单元。
带参数的ReLU(Parametric ReLU,PReLU)引入一个可学习的参数,不同神经元可以有不同的参数。对于第i个神经元,其PReLU的定义为
\begin{equation}
LeakyReLU(x) = \left\{
\begin{array}{ll}
x & \text{if x > 0} \\
\gamma_i x & \text{if x $\le$ 0}
\end{array} \right. \\
=max(0,x) + \gamma_i min(0,x).
\end{equation}
其中$\gamma_i$为$x \le 0$时函数的斜率。因此,PReLU是非饱和函数。如果$\gamma_i = 0$,那么PReLU就退化为ReLU.如果$\gamma_i$为一个很小的常数,则PReLU可以看作带泄露的ReLU.PReLU可以允许不同神经元具有不同的参数,也可以一组神经元共享一个参数。
1.3 ELU
ELU(Exponential Linear Unit,指数线性单元)是一个近似的零中心化的非线性函数,其定义为
\begin{equation}
ELU(x) = \left\{
\begin{array}{ll}
x & \text{if x > 0} \\
\gamma_i(exp(x)-1) & \text{if x $\le$ 0}
\end{array} \right. \\
=max(0,x) + \gamma_i min(0,x).
\end{equation}
其中$\gamma \ge 0$是一个超参数,决定$x \le 0$时的饱和曲线,并调整输出均值在0附近。
1.4 Softplus
Softplus函数可以看作Rectifier函数的平滑版本,其定义为:Softplus(x)=log(1+exp(x)). Softplus函数其导数刚好是Logistic函数.Softplus函数虽然也具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活性。
Swish函数
Swish函数,是一种自门控(Self-Gated)激活函数,定义为:
$swish(x) = x \sigma (\beta x)$
其中$\sigma(·)$为Logistic函数,$\beta$为可学习的参数或一个固定超参数.$\sigma(·) \in(0,1)$可以看作一种软性的门控机制.当$\sigma(\beta x)$接近于1时,门处于“开”状态,激活函数的输出近似于x本身;当$\sigma (\beta x)$接近于0时,门的状态为“关”,激活函数的输出近似于0.
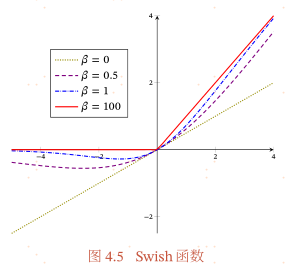
当$\beta = 0$时,Swish函数变成线性函数x/2.当$\beta = 1$时,Swish函数在x>0时近似线性,在x<0时近似饱和,同时具有一定的非单调性.当$\beta \to + \infty$时,$\sigma(\beta x)$趋向于离散的0-1函数,Swish函数近似为ReLU函数.因此,Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数,其程度由参数$\beta$控制.
GELU函数
GELU(Gaussian Error Linear Unit,高斯误差线性单元)也是一种通过门控机制来调整其输出值的激活函数,和Swish函数比较类似.
$GELU(x)=xP(X \le x)$
其中$P(X \le x)$是高斯分布$\mathcal{N}(\mu, \sigma^2)$的累积分布函数,其中$\mu,\sigma$为超参数,一般假设$\mu = 0,\sigma = 1即可$。由于高斯分布的累积分布函数为S型函数,因此GELU函数可以用Tanh函数或Logistic函数来近似,
$GELU(x) \approx 0.5x \Big( 1 + tanh \big( \sqrt{ \frac{2}{\pi} } (x + 0.044715 x^3) \big) \Big)$
或 $GELU(x) \approx x \sigma(1.702x)$
当使用Logistic函数来近似时,GELU相当于一种特殊的Swish函数。
Maxout单元
Maxout单元[Goodfellow et al,2013]也是一种分段线性函数(采用Maxout单元的神经网络也叫作Maxout网络). Sigmoid型函数、ReLU等激活函数的输入是神经元的净输入z,是一个标量.而Maxout单元的输入是上一层神经元的全部原始输出,是一个向量$x=[x_1;x_2; \cdot \cdot \cdot;x_D].$
每个Maxout单元有K个权重向量$w_k \in \mathbb{R}^D$和偏置b_k(1 \le k \le K).对于输入$x$,可以得到K个净输入z_k,$1 \le k \le K$.
$z_k=w_k^Tx+b_k$
其中$w_k=[w_k,1,\cdot \cdot \cdot,w_k,D]^T$为第k个权重向量.
Maxout单元的非线性函数定义为
$maxout(x)=max({z_k})$ , $k \in [1,K]$
Maxout单元不单是净输入到输出之间的非线性映射,而是整体学习输入到输出之间的非线性映射关系.Maxout激活函数可以看作任意凸函数的分段线性近似,并且在有限的点上不可微的.


