index 数据结构与算法
二叉树
二叉树具有五种基本形态:
空二叉树、只有一个根节点、根结点只有左子树、根结点只有右子树、根节点既有左子树又有右子树
特殊二叉树:
- 斜树 斜树一定要是斜的,但是往哪斜还是有讲究。所有结点都只有左子树的二叉树叫左斜树;所有结点都只有右子树的二叉树叫右斜树。这两者统称为斜树
- 满二叉树 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上。
- 完全二叉树 其所有结点与同样深度的满二叉树,它们按层序编号相同的结点,是一一对应的。
二叉树的性质
二叉树有一些需要理解并记住的特性,以便我们更好的使用它。
- 在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
- 深度为k的二叉树至多有2^k -1个结点(k>=1)
- 对任何一颗二叉树T,如果其终端结点数位n0,度为2的结点数为n2,则n0=n2+1
- 具有n个结点的完全二叉树的深度为log_2 n +1
- 如果对一颗有n个结点的完全二叉树(其深度为)的结点按层序编号(从第1层到第层,每层从左到右),对任一结点i(1<=i<=n)
二叉树的存储结构
顺序存储结构
前面谈到树的存储结构,并且谈到顺序存储对树这种一对多的关系结构实现起来比较困难。但是二叉树是一种特殊的树。
由于它的特殊性,使得用顺序存储结构也可以实现。
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,
比如双亲与孩子的关系,左右兄弟的关系等。
先来看看完全二叉树的顺序存储,一颗完全二叉树...
A
B C
D E F G
H I J
将这颗二叉树存入数组中,相应的下标对应其同样的位置,
1 2 3 4 5 6 7 8 9 10
A B C D E F G H I J
当然对于一般的二叉树,尽管层序编号不能反映逻辑关系,但是可以将其按完全二叉树编号,只不过,把不存在的结点设置为"^"而已。
A
B C
^ E ^ G
^ ^ J
1 2 3 4 5 6 7 8 9 10
A B C ^ E ^ G ^ ^ J
虽然可以表示,但会有空间的浪费,对于数据比较多的树来说,树的顺序存储结构一般只用于构建完全二叉树
链式存储结构
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树,每个结点最多有两个孩子,所以它设计一个数据域和两个指针域是比较自然的想法,
我们称这样的链表叫做二叉链表。
typedef struct BiTNode
{
//结点数据
TElemType data;
//左右孩子指针
struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;
就如同树的存储结构中讨论的一样,如果有需要,还可以再增加一个指向双亲的指针域,那样就称之为三叉链表。由于与树的存储结构类似,这里就不详述了。
遍历二叉树
二叉树的遍历方式可以很多,如果我们限制了 从左到右二的 习惯方式,那么主要分为四种:
1.前序遍历 ABDGH-CEIF
2.中序遍历 GDHBAE-ICF
3.后序遍历 GHDBIEFCA
4.层序遍历 ABCDEFGHI
A
B C
D E F
G H I
有同学会说,研究这么多遍历的方法干什么呢?
我们用图形的方式表现树的结构,应该说是非常直观和容易理解,但是对于计算机来说,它只有循环、判断等方式来处理,也就是说,
它只会处理线性序列,而我们刚才提到的四种遍历方法,其实都是在把树中的结点变成某种意义的线性序列,这就给程序实现带来了好处。
另外不同的遍历提供了对结点依次处理的不同方式,可以在遍历过程中对结点进行各种处理。
前序遍历算法
二叉树的定义是递归的方式,所以,实现遍历算法也可以采用递归,而且极其简洁明了。
//二叉树的前序遍历递归算法
void PreOrderTraverse(BiTree T)
{
if(T == NULL)
return;
//显示结点数据,可以更改为其他对节点操作
printf("%c", T->data);
//再先序遍历左子树
PreOrderTraverse(T->lchild);
//再后续遍历右子树
PreOrderTraverse(T->rchild);
}
中序遍历算法
void InOrderTraverse(BiTree T)
{
if (T == NULL)
return;
//中序遍历左子树
InOrderTraverse(T->lchild);
//显示节点数据,可以更改为其他对节点操作
printf("%c", T->data);
//最后中序遍历右子树
InOrderTraverse(T->rchild);
}
后续遍历算法
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
return;
//先后序遍历左子树
PostOrderTraverse(T->lchild);
//在后序遍历右子树
PostOrderTraverse(T->rchild);
//显示结点数据,可以更改为其他对结点操作
printf("%c". T->data);
}
赫夫曼树
压缩优化的二叉树存储结构
赫夫曼编码
为了解决当年远距离通信(主要是电报)的数据传输的最优化问题。通过树结构对字符重新编码
- 将出现频率高的字符放在离根节点近的位置
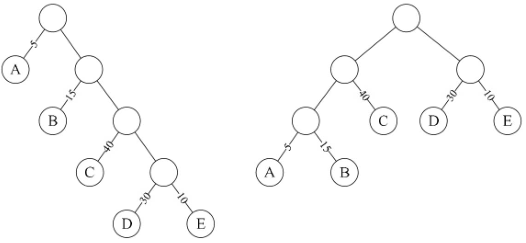
- 使用二叉树路径表示字符编码
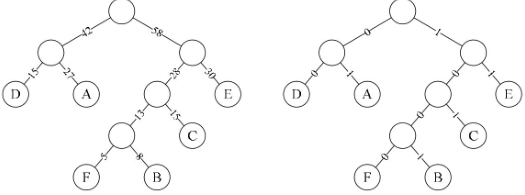
压缩后的编码表
| 字母 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制字符 | 01 | 1001 | 101 | 00 | 11 | 1000 |



