5.字符串

index 数据结构与算法

KMP模式匹配算法

KMP就解决的经典问题是文本串中是否出现过模式串，文本串：aabaabaaf,模式串：aabaaf;暴力匹配算法为两层for循环，时间复杂度O(m*n)

KMP理论原理

前缀表

前缀表即prifix或next数组，是用模式串aabaaf的最长相等前后缀生成的表:

最长相等前后缀	值
a	0
aa	1
aab	0
aaba	1
aabaa	2
aabaaf	0

前缀表next数组

a	a	b	a	a	f
0	1	0	1	2	0

使用前缀表的匹配过程

模式串aabaaf与文本串aabaabaaf在匹配的过程中，模式串的最后f与文本串的b发生不匹配的情况，f前面的子串aabbaa的最长相等前后缀的值为2，即aa是相等的前后缀（公共前后缀），我们直接跳到模式串的下标为2的位置继续匹配，具体匹配的过程如下图所示。

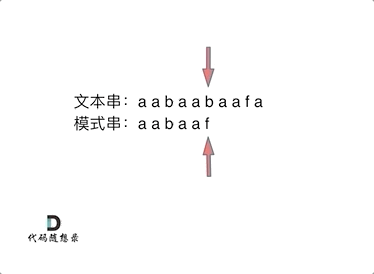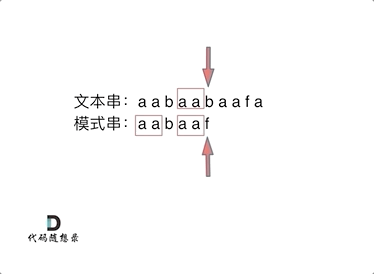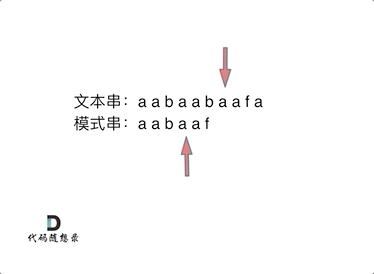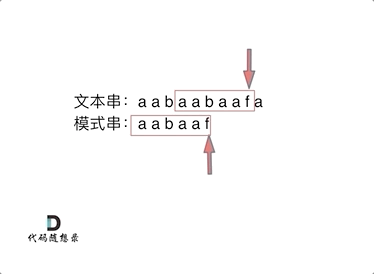
KMP代码实现

前缀表next数组有减1或左移多种实现，下边的代码使用的是原始的前缀表，即没有减1也没左移，只是实现上的不同，思想都是一样的

//定义两个指针i和j，j指向前缀起始位置，i指向后缀起始位置。
class Solution{
public:
  void getNext(int* next, const string& s){  //s为模式串
    int j=0;
    next[0]=0;
    for(int i=1; i<s.size(); i++){
      while(j>0 && s[i]!=s[j]){
        j=next[j-1];
      }
      if(s[i]==s[j]){
        j++;
      }
      next[i]=j;
    }
  }
  int strStr(string haystack, string needle){
    if(needle.size()==0){
      return 0;
    }
    int next[needle.size()];
    getNext(next, needle);
    int j=0;
    for(int i=0; i<haystack.size();i++){
      while(j>0 && haystack[i]!=needle[j]){
        j=next[j-1];
      }
      if(haystack[i]==needle[j]){
        j++;
      }
      if(j==needle.size()){
        return (i-needle.size()+1);
      }
    }
    return -1;
  }
};