BUAA-OO-unit-1-总结

BUAA-OO-unit-1-总结

目录

第一单元主题为对表达式结构进行建模，完成表达式的括号展开与化简。主要学习目标是熟悉面向对象思想和原则，熟悉层次化设计的思想。在第一单元结束之际，对自己的设计思路进行总结，分享心得体会。

第一次作业

代码结构分析

思路与设计依据

第一次作业为简单表达式的建模与去括号、化简。在设计架构的时候，并没有因为单层括号嵌套等约束条件去简化架构，而是充分考虑了架构的可拓展性。

  • 将代码分为互不耦合的两部分：解析与表达式层次结构。

    • 解析部分中，先利用tokenizer进行词元化（如，x**2*-2*(12+x+2*x**2)**2->[x, **, 2, *, -, 2, *, (, 12, +, x, +, 2, *, x, **, 2, ), **, 2]），然后利用递归下降的parser构建层次结构。Tokentype类利用enum存储词元类型。
    • 利用依赖倒转原则，对于factor，分别添加底数Item，指数exponent属性，让常数因子、幂函数因子、表达式因子等都继承自Item类。（常数因子的exponent设置为0即可）

  • 拆括号：定义表达式，项，因子的加法与乘法，对于表达式因子的相乘与幂，按照基准思路展开计算。

  • 深度合并同类项：在Term中设置了系数和余项属性。合并时会利用HashMap，同时递归地重写quals方法，合并时会dfs比较余项。这么做是考虑到了后续出现三角函数，需要合并2*sin(1+x)+3*sin(x+1) 这种情况，因此具体在第二次作业的section中讨论。

uml类图

classDiagram class Calculatable{ <<interface>> } Calculatable <|.. Term Calculatable <|.. Expr Calculatable <|.. Factor Calculatable <|.. Item Calculatable :void + simplify(int) Calculatable :boolean + equals(Object) Calculatable :String + display() class Item { -int signedness +Item(int) +simplify() +display() } class Factor { -Item element; -Const exponent; +Factor(Item element, Const exponent) +simplify(int dep) +deepClone() } class Term{ -int signedness; -boolean ifNeedRemoveParen; -HashSet<Factor> powers -Const coe; -HashMap<Item, Const> hashFactors +Term(HashSet<Factor> powers, Const coe) +Term(ArrayList<Factor> factors, int signedness) +addFactor(Factor factor) +String display() +simplify(int dep) +mergeFactors() +mul(Term obj) +ArrayList<Factor> flatten() +removeParen() +toCeoPowers() } class Expr { -ArrayList<Term> terms -HashMap<HashSet<Factor>, Const> hashTerms +Expr(ArrayList<Term> terms) +addAll(Expr obj) +mul(Expr obj) +replace(HashMap<Var, Factor> table) +simplify(int dep) } class ExprFactor { -Expr expr +ExprFactor(Expr expr) } class Const { -BigInteger num +Const(int signedness, BigInteger num) +mul(Const obj) +add(Const obj) +pow(Const exp) } class Var{ -String varName +Var() +Var(String varName) } class Tokenizer{ -ArrayList<Token> tokens -String expression +ArrayList<Token> getTokens() -isWhitespace(char c) } class Token { -BigInteger num; -TokenType tokenType; -String name; +Token(BigInteger num, TokenType tokenType) +Token(String name, TokenType tokenType) +Token(TokenType tokenType) +String toString() } class Parser{ -ArrayList<Token> tokens -int tokenIdx +Parser(ArrayList<Token> tokens) +parseExpr() Expr +parseTerm() Term +parseFactor() Factor +parseConst() Const } class MainClass Item <|-- ExprFactor Item <|-- Const Item <|-- Var Token <.. Tokenizer Tokenizer <.. Parser Parser <.. MainClass Expr <.. MainClass

基于度量的代码分析以及优缺点

  • 方法复杂度

    method CogC ev(G) iv(G) v(G)
    Tokenizer.getTokens() 28.0 15.0 21.0 21.0
    Term.display() 20.0 1.0 6.0 10.0
    Parser.parseFactor() 16.0 6.0 7.0 10.0
    Parser.parseExpr() 10.0 4.0 6.0 7.0
    Term.toCeoPowers() 9.0 1.0 7.0 8.0
    Parser.parseTerm() 8.0 4.0 8.0 9.0
    Term.numOfExprFactor() 7.0 1.0 7.0 7.0
    Term.removeParen() 5.0 1.0 4.0 4.0

  • 类复杂度

    class OCavg OCmax WMC
    Const 1.4545454545454546 3.0 16.0
    Expr 2.272727272727273 7.0 25.0
    ExprFactor 1.3333333333333333 3.0 8.0
    Factor 1.4285714285714286 3.0 10.0
    Item 1.3333333333333333 3.0 8.0
    MainClass 1.0 1.0 1.0
    Parser 5.0 8.0 25.0
    Term 3.0555555555555554 9.0 55.0
    Token 4.0 13.0 16.0
    Tokenizer 6.333333333333333 16.0 19.0
    Var 1.0 1.0 4.0

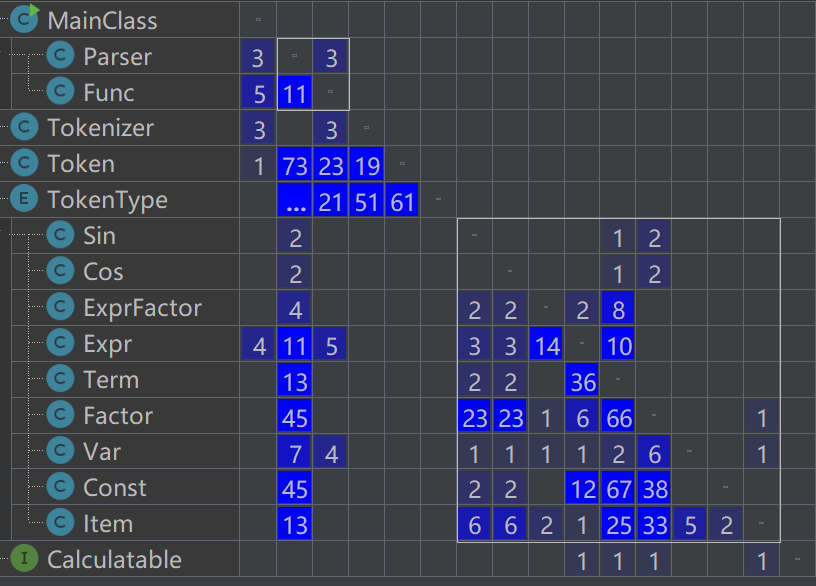
  • 类关联矩阵

    image

  • 优点：对类与方法复杂度进行分析，可以发现复杂度较高的方法主要集中在词元化，解析这些方面，会出现较多分支结构。其余部分方法复杂度较低，基本做到了高内聚，低耦合。

  • 缺点：由于考虑到后续作业，代码长度较长。对于第一次表达式内部的关联矩阵来看，项和表达式，常数和项，因子和项的关联度很高，这是因为，出现了循环依赖的情况；且由于将项提取了系数，导致常数与项依赖较高。由此可见，在表达式和项的层面，还没有充分应用依赖倒转原则，层次安排较不灵活。

测试思路与策略

  • 评测机的开发

    • 第一次作业，利用python的popen与sympy实现了评测机的构建。

    • 评测机分为多项目自动编译，自动评测两部分。

    • 使用subprocess，自动寻找主类，编译加入FILELIST，利用文件list实现多项目的编译，便于互测使用。

    • 主要评测逻辑:

      • 测试得到答案

        os.chdir(DIR)
    x = sympy.Symbol('x')
    #try:
    myAnswer = os.popen('echo ' + fx + '|java ' + NAME)
    myAnswer = myAnswer.read().split("\n")[0]

      • 判定正误

        tureValue = sympy.sympify(sympy.expand(fx))
    myValue = sympy.sympify(myAnswer)

    if myValue == tureValue:
    	#output
    else:
    	#output

  • 数据生成策略

    • 按照递归下降生成即可，比较简单。注意，在dfs时应记录深度与幂次，防止非法。
    • 同时可以利用常量池生产常数，借此进行cornercase、极限情况的测试。

bug与评测分析

  • 在互测与强测中未出现bug。
  • hack的策略为随机数据+缩小范围。利用随机数据发现bug，再手动缩小bug范围。两位同学的bug，一位在处理+1*x时出现了输出1x的问题，另一位在处理前导零时出现了问题。

第二、三次作业

由于第二、三次作业的代码改动不足十行，因此放在一起叙述。

代码结构分析

UML类图与架构

  • 第二次作业在第一次的基础上增加了三角函数，求和函数，以及自定义函数调用，难点主要集中在变量-因子的替换，添加了三角函数后如何深度合并同类项，三角优化这几个方面。

  • 全部代码UML类图如下:

    classDiagram class Calculatable{ <<interface>> } Calculatable <|.. Term Calculatable <|.. Expr Calculatable <|.. Factor Calculatable <|.. Item Calculatable :void + simplify(int) Calculatable :boolean + equals(Object) Calculatable :String + display() Calculatable :replace(HashMap<Var, Factor> table) class Item { -int signedness +Item(int) +replace() +simplify() +display() } class Factor { -Item element; -Const exponent; +Factor(Item element, Const exponent) +simplify(int dep) +replace(HashMap<Var, Factor> table) +deepClone() } class Term{ -int signedness; -boolean ifNeedRemoveParen; -HashSet<Factor> powers -Const coe; -HashMap<Item, Const> hashFactors +Term(HashSet<Factor> powers, Const coe) +Term(ArrayList<Factor> factors, int signedness) +addFactor(Factor factor) +String display() +simplify(int dep) +mergeFactors() +mul(Term obj) +ArrayList<Factor> flatten() +removeParen() +toCeoPowers() +replace(HashMap<Var, Factor> table) } class Expr { -ArrayList<Term> terms -HashMap<HashSet<Factor>, Const> hashTerms +Expr(ArrayList<Term> terms) +addAll(Expr obj) +mul(Expr obj) +replace(HashMap<Var, Factor> table) +simplify(int dep) } class Sin { -Factor factor +Sin(Factor factor) } class Cos { -Factor factor +Cos(Factor factor) } class ExprFactor { -Expr expr +ExprFactor(Expr expr) } class Const { -BigInteger num +Const(int signedness, BigInteger num) +mul(Const obj) +add(Const obj) +pow(Const exp) } class Var{ -String varName +Var() +Var(String varName) } class Tokenizer{ -ArrayList<Token> tokens -String expression +ArrayList<Token> getTokens() -isWhitespace(char c) } class Token { -BigInteger num; -TokenType tokenType; -String name; +Token(BigInteger num, TokenType tokenType) +Token(String name, TokenType tokenType) +Token(TokenType tokenType) +String toString() } class Parser{ -ArrayList<Token> tokens -HashMap<String, Func> functions -int tokenIdx +Parser(ArrayList<Token> tokens, HashMap<String, Func> functions) +Parser(ArrayList<Token> tokens) +parseExpr() Expr +parseTerm() Term +parseFactor() Factor +parseSum() Factor +parseFun() Factor +parseTriangle(TokenType tokenType) Factor +parseConst() Const } class Func{ -ArrayList<Var> vars -String funcName -Expr expr +parse(String definition) +deepClone() Func } class MainClass Item <|-- Sin Item <|-- Cos Item <|-- ExprFactor Item <|-- Const Item <|-- Var Parser <.. MainClass Expr <.. MainClass Token <.. Parser Func <.. Parser Expr <.. Parser Tokenizer <.. Token

  • 架构

    • 沿袭了第一次作业的架构，分为不互相耦合的两部分：解析部分和表达式层次结构。
    • 解析部分中，先利用tokenizer进行词元化，然后利用递归下降的parser构建层次结构。Tokentype类利用enum存储词元类型。
    • 对于factor，分别添加底数Item，指数exponent属性，让常数因子、幂函数因子、三角函数因子、表达式因子等都继承自Item类。（常数因子的exponent设置为0即可）

基于度量的代码分析以及优缺点

  • 类复杂度

    class OCavg OCmax WMC
    Const 1.5 3.0 18.0
    Cos 1.5714285714285714 4.0 11.0
    Expr 2.3636363636363638 7.0 26.0
    ExprFactor 1.2857142857142858 3.0 9.0
    Factor 2.0 5.0 18.0
    Func 2.1666666666666665 8.0 13.0
    Item 1.2857142857142858 3.0 9.0
    MainClass 2.0 2.0 2.0
    Parser 5.333333333333333 12.0 48.0
    Sin 1.5714285714285714 4.0 11.0
    Term 2.75 9.0 55.0
    Token 3.4285714285714284 18.0 24.0
    Tokenizer 7.666666666666667 20.0 23.0
    TokenType 0 0 0.0
    Var 1.5 4.0 9.0
    Average 2.4642857142857144 7.285714285714286 18.4

  • 方法复杂度（这里只列出复杂度较高的方法）

    method CogC ev(G) iv(G) v(G)
    Tokenizer.getTokens() 35.0 19.0 31.0 31.0
    Term.display() 20.0 1.0 6.0 10.0
    Parser.parseTriangle(TokenType) 17.0 4.0 4.0 6.0
    Func.parse(String) 16.0 7.0 10.0 12.0
    Parser.parseFactor() 16.0 7.0 10.0 14.
    Parser.parseSum() 11.0 6.0 6.0 11.0
    Parser.parseExpr() 10.0 4.0 6.0 7.0
    Parser.parseFun() 10.0 6.0 3.0 6.0
    Term.toCeoPowers() 7.0 1.0 4.0 5.0
    Parser.parseTerm() 6.0 3.0 4.0 5.0
    Term.numOfExprFactor() 5.0 1.0 5.0 5.0
    Term.removeParen() 5.0 1.0 4.0 4.0

  • 关联矩阵

    image

  • 本次作业代码较长，有效行数约有1200行，但是每个方法行数基本控制在50行以内。

  • 优点：对类与方法复杂度进行分析，可以发现复杂度较高的方法主要集中在词元化，解析这些方面，会出现较多分支结构。其余部分方法复杂度较低，基本做到了高内聚，低耦合。加入了三角函数类以后，耦合程度、复杂程度并没有明显提高，可见架构可拓展性很好。

  • 缺点：表达式内部的关联矩阵来看，项和表达式，常数和项，因子和项的关联度很高，这是因为，出现了循环依赖的情况；且由于将项提取了系数，导致常数与项依赖较高。这是因为在表达式和项的层面，还没有充分应用依赖倒转原则，层次安排较不灵活。

设计依据与难点思路

  • 深度合并同类项

    • 我在第一次作业中就利用HashMap实现了深度合并同类项，分别在Term、Expr类中实现了相应的合并方法，因此此次作业改动较小。

    • 事实上，Term、Expr中合并的方法是非常相似的，Term中对因子的合并主要依赖 HashMap<Item, Const> hashFactors，Key为Factor的底数，Value为指数。Expr中对项的合并主要依赖 HashMap<HashSet<Factor>, Const> hashTerms，Key为用HashSet表示的项的除去系数的部分，Value为系数。

      • 当发生hash冲突，需要合并的时候，Term的指数相加，Expr的系数相加。

        • 举个例子：假设在Expr中，已有一个ArrayList<Term> terms，创建 HashMap的时候可以利用 Collectors.toMap() 方法，在key重复的时候，可以利用 Const.add()方法。

          hashTerms = terms.stream().collect(Collectors.
                    toMap(Term::getPowers, Term::getCoe, Const::add, HashMap::new));
    • 重写 equals() 方法，利用dfs进行余项的比较。注意应比较HashSet等无序容器，从而可以合并2*sin(1+x)+3*sin(x+1) 这种情况
    • 出现三角函数时无需特殊处理，直接HashMap合并即可。

  • 变量-因子的替换

    • 求和函数和自定义函数调用的核心都是变量-因子的替换。并没有使用正则表达式等字符串替换策略；而是按层次结构建立自定义函数类，在递归下降解析的过程中对sum，functions替换。

    • 在解析的时候，遇到需要替换的情况就立刻替换。

    • 在所有表达式结构相关类中递归地实现Replace方法，要替换是传入 HashMap<Var, Factor> 作为参数，key是变量类，表示自定义函数中待替换变量，Value为因子类，表示要替换成的因子。

    • 在Factor类中实现对表达式的更改，例如，对 y**2 做替换 y->x**3 时，先合并指数，再替换底数。对替换成常数的情况需要特判，进行乘方运算，防止常数出现指数。例如，对 y**2 做替换 y->3 时，结果为 9 。

  • 深克隆：重复调用自定义函数，求和函数对因子的重复替换

    • 先让相应类实现Serializable序列化接口

    • 然后利用字节序列输出流将对象序列化成字节序列，将要序列化的对象写入

    • 再利用对象输入流传入字节序列，反序列化到一个新对象里就实现了深拷贝。

    • public Factor deepClone() {
        Factor res = null;
        try {
            ByteArrayOutputStream bo = new ByteArrayOutputStream();
            ObjectOutputStream oo = new ObjectOutputStream(bo);
            oo.writeObject(this);
            oo.close();
            ByteArrayInputStream bi = new ByteArrayInputStream(bo.toByteArray());
            ObjectInputStream oi = new ObjectInputStream(bi);
            res = (Factor) oi.readObject();
            oi.close();
        } catch (Exception e) {
            System.out.println(e.getMessage());
        }
        return res;
    }

    • 注意：一定要让待拷贝对象属性中所有涉及的类都实现Serializable序列化接口，否则无法正常拷贝

优化策略

​ 着重考虑 $$ sin→cos$$，$$ sin→cos$$ 的情况。

  • 可以按照正弦余弦建立两个HashMap，将表达式中含有 sin(x)**2 和含有 cos(x)**2 到分别添加至 HashMap<HashSet<Factor>, Const> 中，寻找两个HashMap key相等的情形，进行合并。

数据生成，自动评测

  • 自动评测系统的主要部分沿用第一次作业，评测的逻辑发生变化：即使用原始生成的数据喂给java程序，使用处理过的数据喂给sympy，进行比对。
    • 比较遗憾的一点，由于时间关系，没能实现对输出数据是否包含不必要括号的检测。这一部分没能hack，自测也没能做到自动化进行。
  • 数据生成的每个递归模块分别生成两种字符串，一种生成给java程序，另一种会对sum与functions进行替换-得到能被sympy处理的数据。

bug与评测分析

  • 第二次作业
    • 强侧与互测做到了bugfree。
    • 自测发现深克隆相关的bug，一个出现在三角函数化简中，另一个出现在重复调用函数中。（由此可见不可变对象有其好处）。
    • 互测发现两位同学的bug，一位同学在处理符号时出错，另一位同学在处理指数时，会将x ** 46*+69 处理为 69*x**4 。
  • 第三次作业
    • 互测强测同样未出现bug
    • 自测时发现一个bug，在处理sin((1+x)**2) 时会输出 sin((1+x)**2) 。但是强测似乎并没有考察这个点？
    • 互测发现三处bug，分别与sum的上下界、三角函数化简有关。

体验与心得

  • 性能与功能的tradeoff

    • 实际项目的开发绝非算法竞赛，在不影响代码结构，并且保证复杂度能在一定范围的前提下，可以适当优化性能。但是当优化引入极高复杂度，并可能对功能（即正确性）造成影响时，则应有所取舍。
    • 以不可变对象为例，这种思想能减少深克隆出错的概率，但是在空间上显然不是最优解。对于oo的课程来分析，还是应该为了bugfree权衡掉空间开销。
    • 最近被一个工业界大佬教育，对方表示在项目开发中更会注重功能而非优化，也算是一点insight吧。

  • 迭代开发中，最重要的或许就是一个好的架构

    • 第一单元在设计是特意考虑了可拓展性。这样一来，第二次作业对化简的核心逻辑几乎没有改动，仅对函数与sum的替换增加了100行左右的代码。而第三次作业的改动则在10行以内。
    • 在架构上，还是存在不少遗憾。在第二第三单元的开发中，为了不大改第一单元的架构，防止引入新的bug，而没有充分的尝试其他可能更优的架构。比如，本次作业在表达式和项的层面还没有充分实现依赖倒转原则，使得化简的逻辑较为复杂。

  • 最后，要感谢在讨论区积极分享的同学们，在我解决数据生成等问题中提供了巨大的帮助。也期望在今后的学习中与大家多多交流~

posted @ 2022-03-25 23:40  gnwekge  阅读(61)  评论(0)  编辑  收藏  举报