近似推断（1）

概率模型的应用：

1.中心任务：在给定观测变量X的条件下，计算潜在变量Z的后验概率分布p(Z|X)，以及关于p的期望。

2.任何未知的参数都有一个先验概率分布

eg：对于EM算法来说我们需要计算完整数据的对数似然函数关于潜在变量Z的后验概率分布的期望。

但在实际情况下，求解许多模型的后验概率分布或者计算关于这个后验概率分布的期望是不可行的（原因：潜在空间维度太高，或者后验概率分布的形式特别复杂，导致不能直接计算以及期望无法解析地计算）

因此我们需要借助近似推断：

近似方法：变分推断/变分贝叶斯，使用了更加全局的准则并被用于广泛的实际应用中（假设后验分布有一个具体的参数形式）。

讨论：变分最优化的概念如何应用于推断问题：

假设：我们有一个纯粹的贝叶斯模型，其中每个参数都有一个先验概率分布，将这个模型的潜在变量以及参数组成的集合记作Z。观测变量的集合记作X。我们可能有N个独立同分布的数据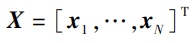且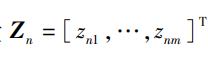。我们的概率模型确定了联合概率分布，我们的目标是找到对后验概率分布p（Z|X）以及模型证据p(X)的近似。。

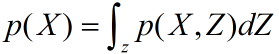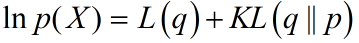
其中通过推导下界可以通过期望的形式进行表示：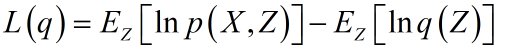

 

我们通过关于q(Z)的最优化来使下界L(q)达到最大值，等价于最小化KL散度，（用简单的分布q(Z)来近似p(Z|X)后验分布用，简单分布的均值来代替复杂的分布的均值）。如果我们允许任意选择q(Z)，那么下界的最大值出现在KL散度等于0的时候，此时q(Z)等于后验分布p(Z|X)，然而，假定在需要处理的模型中，对真是的概率分布进行操作是不可行，因此考虑概率分布q(Z)的一个受限制的类别。我们考虑的方法是限制概率分布q(Z)的范围。假设我们将Z的元素划分成若干个不相交的组。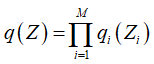（这个分解形式对应于物理学中的一个近似框架，平均场理论）

在所有具有分解形式的概率分布q(Z)中，我们现在寻找下界最大的概率分布，于是我们希望对下界关于所有的概率分布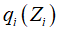进行一个自由形式的（变分）最优化。通过关于每个因子进行最优化来完成整体的最优化过程。（未完待续）