算法笔记-完全二叉树个数计算(时间复杂度小于O(n))

------------恢复内容开始------------

　　首先科普一个事实，对于一个满二叉树来说，节点个数=（1<< (高度))-1。

接下来我们看这道题，管他三七二十一，前面那么多树的遍历，直接搞起，可他丫的还有一个限制条件：时间复杂度小于O(n)，那就把这条路堵死了，算了算了，先看图分析一下：

 

 

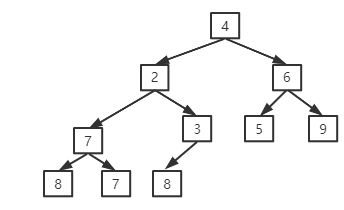
 我们仔细观察可以发现，完全二叉树的左右子树必有一个为满二叉树对于4：右子树，对于2：左子树，对于3左子树只有一个节点，单个节点也是满二叉树，分析到这里大体思路是有了，还有一个问题就是如何判断当前哪边是满二叉树？有一个小技巧：看右子树的最左节点高度是否和整棵树一样，代码如下：

public static int CTNum(Node node){

        if(node == null){
            return 0;
        }

        return CTNum(node,deep(node,0),0);
    }

    public static int CTNum(Node node,int deep, int level){
        if(deep == level){
            return 1;
        }

        if(deep(node.right,level+1) == deep){  
            return CTNum(node.right,deep,level+1) + (1<<(deep-level));
        }else{
            return CTNum(node.left,deep,level+1) + (1<<(deep-level-1));
        }
    }

    private static int deep(Node right, int level) {
        while(right != null){
            level++;
            right = right.left;
        }
        return level-1;
    }

这里满二叉树在左边和右边有一个区别，因为是从左向右排的，若在右边，则会少一行。