算法笔记-判定是否完全二叉树

　　老规矩，先看定义：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树

　　在解释：其实就是和堆一样的，一棵树从上到下从左到右必须要完完整整的按顺序来，描述的不太容易理解，来个看图说话吧：

 

 

 

 

 

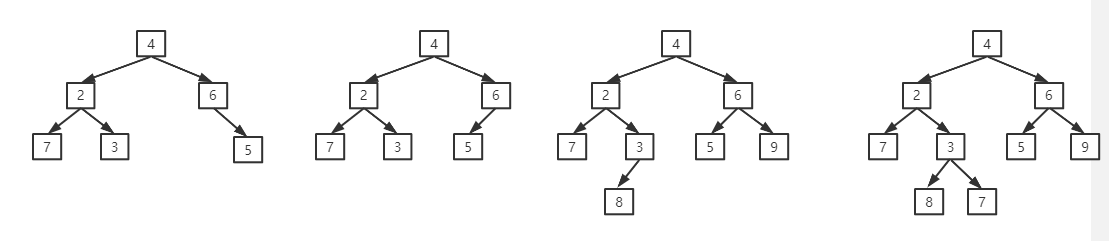
 请问上图从左到右四个二叉树，哪个是完全二叉树？答案是第二个，因为其他的基本上都不满足从左到右一个个插入，总是喜欢漏一个两个的，逼死强迫症。

了解了什么是完全二叉树，光肉眼能看出来没用啊，得计算机识别，那咋识别呢，我们来分析一下，完全二叉树按顺序遍历的话，任一节点必须是左右子树顺序排列的，一旦有一个没用则后续都不可以再有子树，可是如上图二有左节点没用右节点也是符合的，因此我们需要分为两种情况：

1.有右子树没有左子树，这种可以直接判定不满足

2.若没有任一子树，后续任一节点有任一子树都说明不满足

带着这两个条件我们撸代码：

public static boolean isCompleteTree(Node head){
        boolean isleaf = false;

        Queue<Node> queue = new LinkedList<>();
        queue.offer(head);
        while (!queue.isEmpty()){
            Node node = queue.poll();
            if((node.left == null && node.right != null)   //条件一
            ||
                    (isleaf && (node.left != null || node.right != null))){  //条件二
                return false;
            }

            //这里只需判断没有右子树，后续节点不能有子树，
            // 因为若有右子树而没有左子树，则满足条件一，直接被拦截
            if(node.left != null){
                queue.offer(node.left);
            }

            if(node.right != null){
                queue.offer(node.right);
            }else{
                isleaf = true;
            }
        }
        return true;
    }

这里使用isleaf变量控制是否开启无子节点筛选。