算法笔记-寻找二叉树的前后置节点
我们前面写过二叉树的前序,中序,后续遍历算法,今天聊到的前后置节点就是对于中序遍历来说的顺序前后节点,如下图是按中序遍历顺序1-10的节点:
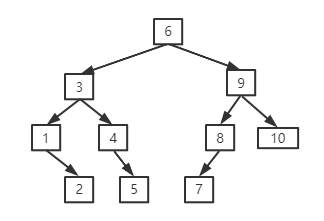
比如3的前置节点为2,后置节点为4,我们先来看看后置节点的算法思想:
我们都知道中序遍历是按照节点左-父-右顺序遍历的,因此一个节点的后置节点只会有两种情况:1.在右子节点的所在的树上,2.当前节点所在位置处于某一父(可能是祖父,曾祖父,这里统称父)节点的左子节点的树上,否则肯定是不存在的,我们在细分析这两点:
1:右子节点所在树上有很多节点,那么我们如何知道具体是哪个节点呢?其实这个问题我们可以换个角度:我们如何找到右子节点树上的第一个节点,这个答案就显而易见了:最左节点
2:细评第二种情况之前我们可以先思考一个问题,中序遍历时,如果当前节点已经是某一结点的最右节点,那么这个节点是否是这个节点下面的遍历最后的一个节点?答案是肯定的,那么我们只能继续往上找父节点,如果这个节点在父节点的右节点上,那说明对于父节点所在的树上,依旧是最右节点,直到找到这个在父节点的左节点时,说明这个父节点是这整个树的后置节点,而这个数最后一个节点就是我们选中的节点,那么不正说明这个节点的后置节点是最后找到的这个父节点吗。
理解起来可能有点繁杂,这里我对中序遍历也做一个升华:理解中序遍历时,不要局限于某个点,比如对于根节点来说,左子树相当于左,右子树相当于右,而左-父-右的顺序对于这一整颗树来说则是左子树-根节点-右子树,对于下面的子树也是一样的道理,这样就可以把无数个小的行为概括成一个大的行为,同样对于每一个子树也是这样一个个大的行为。我们在找后置节点时其实就是在考虑两个问题:1.该节点作为某一颗子树的根节点,那么我们就找这一颗子树的右节点的第一个遍历的点,2.作为左子树上的最后一个节点,那么我们就需要找到这个节点作为找到的父节点左子树的最后一个节点(也是最右节点),这样就好理解多了。
说了那么多,还是用代码来看:
public static Node getNextNode(Node node){ if(node == null){ return null; } if(node.right != null){ return findLeftNode(node.right); }else{ Node parent = node.parent; while(parent != null && node != parent.left){ node = parent; parent = parent.parent; } return parent; } }
private static Node findLeftNode(Node right) { while(right.left != null) right = right.left; return right; }
如果可以理解上面的思想,代码还是很简单的。
如果可以理解后置节点,前置节点也是一样的道理,我们就可以直接看中序遍历顺序:左-父-右,那么我们也可以分为两种情况:1.作为父节点,那么前置节点一定在左子树上,只需要找到左子树最后一个点(最右节点) 2.作为右节点,那么我们只需要找到以该节点为右子树的最左节点的最大树父节点(也就是第一个将该节点所在子树作为右子树的节点),代码如下:
public static Node getPreNode(Node node){ if(node == null){ return null; } if(node.left != null){ return findRightNode(node.left); }else{ Node parent = node.parent; while (parent!= null && node != parent.right){ node = parent; parent = parent.parent; } return parent; } }
private static Node findRightNode(Node left) { while(left.right != null) left = left.right; return left; }



