算法笔记-堆排

　　学习堆排之前先学习一下堆得数据结构，我们常用的一般分为小顶堆和大顶堆，我们以大顶堆为例：

  

 

 

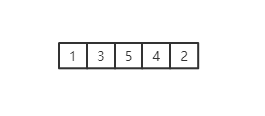
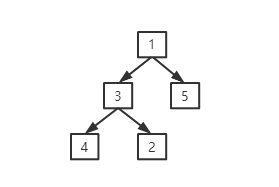
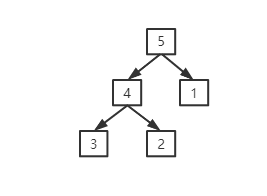
 上面从左到右分别是数组，数组转成堆得形式，其实就是一个完全二叉树，而最右边这个可以看到每个节点相对所有子节点来说都是最大的，这就是大顶堆，同理，小顶堆反之（这块不理解的可以看我之前写的一篇文章：https://www.cnblogs.com/gmt-hao/p/14417541.html），而我们这里的堆是数组实现的，数组的子节点和父节点的关系：假设父节点的下标为a, 左子节点大小为2*a+1 ,右子节点下标为2*a+2，假设任一子节点下标为b,而父节点的都是(b-1)/2,带着这些认识我们来看看堆得形成。

堆排的前提是先将数组构造成一个小顶堆或者大顶堆，我们这里还是以大顶堆为例，那么构造时就会出现两个情况：

　　1.当前插入数比父节点大，则需要一直往上交换，直到满足大顶堆规则

　　2.当前插入节点比子节点小，则需要往下将子节点中较大的数换上来

那么我们就先来实现一下这两种情况代码：

/**
     * 将数组中index下标的元素插入堆
     */
    private static void heapInsert(int[] arr,int index){
        while(arr[index] > arr[(index-1)/2]){
            swap(arr, index, (index-1)/2);
            index = (index-1)/2;
        }
   

这段代码太简单了，首先看while判断，其实就是看当前节点和父节点大小，若比父节点大则交换，并将当前节点下标index置为父节点下标,继续和父节点比，直到不比父节点大或者没有父节点为止。

再看当前节点比子节点小时：

 private static void heapify(int[] arr,int index, int size){
        int l = index*2 +1;
        
        //递归方式
        if(l < size) {
            int r= l+1;
            int largest = r > (size -1) || arr[r] < arr[l] ? l : r;
            if(arr[index] < arr[largest]){
                swap(arr, index, largest);
                heapify(arr,largest,size);
            }
        }

        //循环方式
        while(l<size){
            int r= l+1;
            int largest = r > (size -1) || arr[r] < arr[l] ? l : r;
            if(arr[index] >= arr[largest]){
                break;
            }
            swap(arr, index, largest);
            index = largest;
            l = index*2 +1;
        }
    }

这里两个版本，上面的递归方式是我自己理解着去写的，但是后来看到别人的循环方式，可以减少压栈次数，而且更加优雅。其实理解起来都不难，首先找出子节点中较大的值，与自己比较大小，将较大的替换上来，继续往下递归(循环)。

那么堆排又是怎么做到的呢，其实有了heapInsert我们就可以将数组构造成堆了，那么如何利用堆来进行排序呢：

 

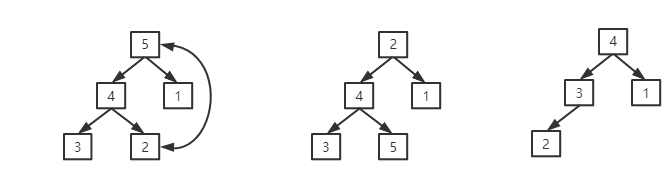
 如上图所示，先将根节点(最大的)和最后一个交换，这样最后一个节点就是最大的数，再把堆大小缩小一个，再将堆构造成大顶堆（这样最大的数不会动），循环到最后一个数，则可以保证数组有序。代码如下：

public static void heapSort(int[] arr){
        //数组构造大顶堆
        for(int i=0;i<arr.length;i++){
            heapInsert(arr,i);
        }

        int size = arr.length;
        //交换
        for(int j=0;j<arr.length;j++){
            swap(arr, 0, arr.length-j-1);
            heapify(arr,0,--size);
        }

    }

其实这种方式感觉和冒泡排序有点类似(都是每次找一个最大值嘛)，只不过每次heapify的复杂度只有O(logN)。