2022 Hubei Provincial Collegiate Programming Contest G. Brick(gym103729)
大意
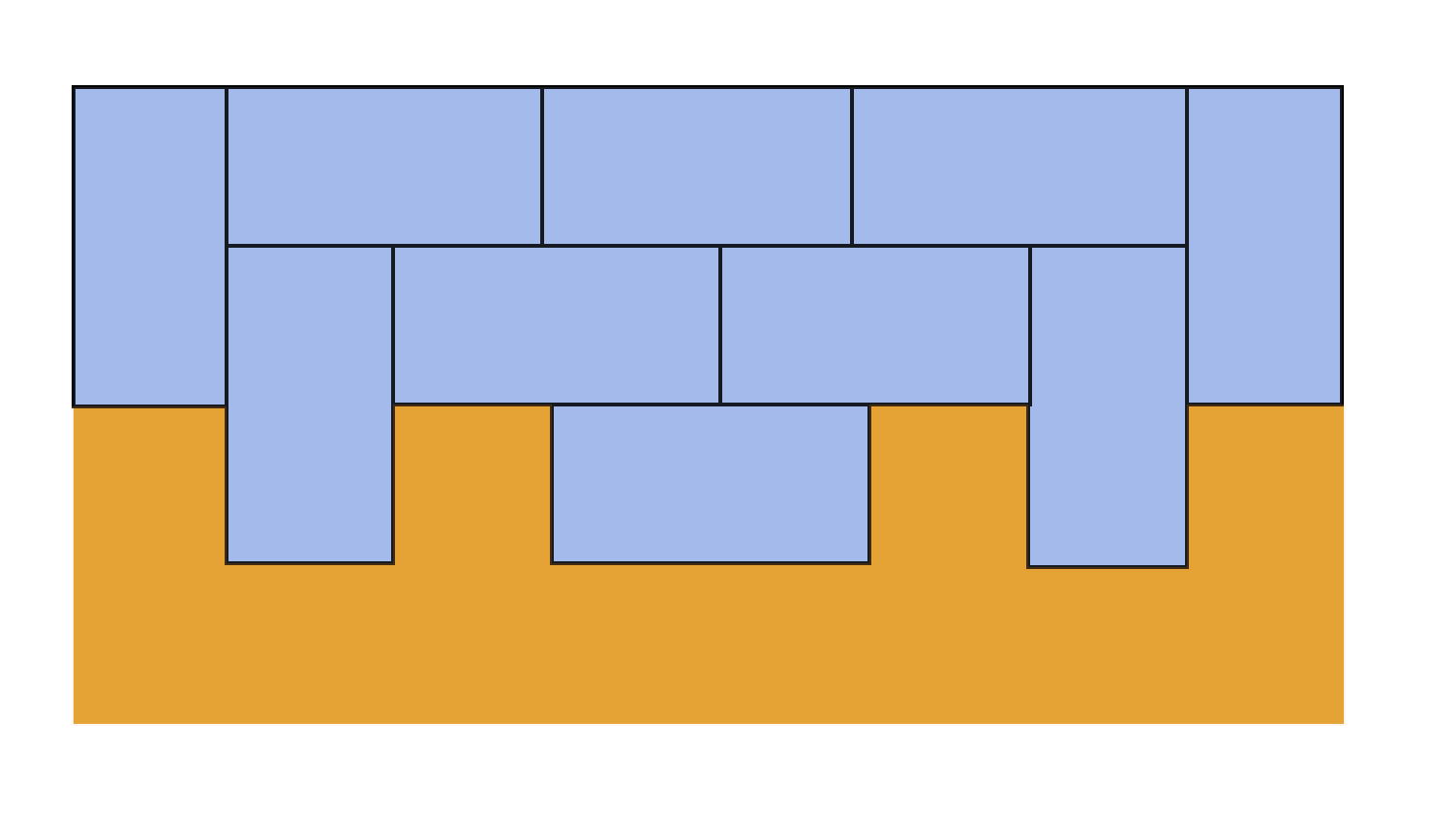
给出底层高度,用1*2的砖块将总形状铺成等高矩形,使得高度最小(不能放在外面)
题解
奇妙做法
当高度同奇偶时显然x可以的话x+2也可以,直接加一层竖的,所以首先分奇偶二分高度
有解的必要条件1是,把矩形黑白方格染色之后未填的黑=白(一个1*2刚好覆盖1黑1白)
然后从左往右放砖块,可以感受一下发现把当前列尽量往上拉是最优的
比如二分ans=10,初始h=4,3,2,1,1
那么往右扫过去可以依次拉到10,9,8,7高度;接下来把h[5]拉到7之后又可以整体横着放一波,变成10,10,10,9,8的阶梯
于是维护阶梯的最下端高度hnow,当h[i]和hnow不同奇偶时可以拉到hnow-1,否则拉到hnow之后再整体往上拉变成hnow+1
这样从左往右知道hnow<h[i],此时无论如何也无法拉成阶梯状,记录终止位置i
然后求出从右往左的终止位置j,若j<i则有解
感受一下就是可以从左往右和从右往左拉出两个阶梯,然后剩下由于必要条件1剩下一定合法(
最后再打表感受一下发现ans不超过max(h[i])+1,所以不用二分了(
code
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define ll long long
#define file
using namespace std;
int n,i,j,k,l,mx;
int h[200001];
ll L,R,Mid,ans;
bool pd(ll t)
{
int i,j;
ll sum=0,h1=t,h2=t;
if (t<mx) return 0;
fo(i,1,n)
{
if (i&1)
{
if ((t-h[i])%2==1)
++sum;
}
else
{
if ((t-h[i])%2==1)
--sum;
}
}
if (sum) return 0;
fo(i,1,n)
{
if (h1>=h[i])
{
if ((h1-h[i])%2==0)
h1=min(h1+1,t);
else
--h1;
}
else
break;
}
fd(j,n,1)
{
if (h2>=h[j])
{
if ((h2-h[j])%2==0)
h2=min(h2+1,t);
else
--h2;
}
else
break;
}
if (j<i) return 1;
else return 0;
}
int main()
{
// freopen("G.in","r",stdin);
scanf("%d",&n);
fo(i,1,n) scanf("%d",&h[i]),mx=max(mx,h[i]);
// printf("%d\n",pd(10));
ans=2000000000;
L=1,R=2000000000;
while (L<R)
{
Mid=(L+R)/2;
if (!pd(Mid*2-1))
L=Mid+1;
else
R=Mid;
}
ans=min(ans,L*2-1);
L=1,R=2000000000;
while (L<R)
{
Mid=(L+R)/2;
if (!pd(Mid*2))
L=Mid+1;
else
R=Mid;
}
ans=min(ans,L*2);
if (ans==2000000000) ans=-1;
printf("%lld\n",ans);
}


