整数划分的快速计算(loj#6268. 分拆数)
上午听WC的时候听到的并没有细讲的东西
整数划分
n很小的时候是入门级别的东西,设f[i][j]表示总和为i个数为j的方案,每次加上一个1或者对全部的+1
考虑答案的生成函数:
\(\prod_{i>=1} \sum_j x^{ij}=\prod_{i>=1}\frac{1}{1-x^i}\)
i的范围是1~n没法分治ntt求,所以对式子取ln,最后再exp回来
\(=\sum_{i>=1}\ln\frac{1}{1-x^i}\)
\(=-\sum_{i>=1}\ln(1-x^i)\)
关于\(\ln(1+x)\)的麦克劳林级数(泰勒展开x0=0的特殊情况):
\(\ln(1+x)=\sum_i \frac{(-1)^{i-1}x^i}{i}\)
UPD:以下是智障方法,正常方法见后文
先证明一些东西:\(((1+x)^n)'=n(1+x)^{n-1}\)以及\(f(x)=\ln(1+x),f^{(n)}(x)=(-1)^{n-1}(n-1)!(1+x)^{-n}\)
第一条有\((1+x)^n=\sum \binom{n}{i}x^i,((1+x)^n)'=\sum \binom{n}{i}ix^{i-1}=n(1+x)^{n-1}\)
第二条考虑归纳
已知\(f^{(n-1)}(x)=(-1)^{n-2}(n-2)!(1+x)^{-(n-1)}\),则根据u/v=(u'v-v'u)/v^2有
\(f^{(n)}(x)=((-1)^{n-2}(n-2)!(1+x)^{-(n-1)})'=(\frac{(-1)^{n-2}(n-2)!}{(1+x)^{2n-2}})'\)
\(=-\frac{((1+x)^{n-1})'(-1)^{n-2}(n-2)!}{(1+x)^{2n-2}}=-\frac{(n-1)(1+x)^{n-2}(-1)^{n-2}(n-2)!}{(1+x)^{2n-2}}=(-1)^{n-1}(n-1)!(1+x)^{-n}\)
现在证明\(\ln(1+x)=\sum_i \frac{(-1)^{i-1}x^i}{i}\):
\(\ln(1+x)=f(x)=\sum_i \frac{f^{(i)}(0)x^i}{i!}=\sum_i \frac{(-1)^{i-1}(i-1)!x^i}{i!}=\sum_{i>=1}\frac{(-1)^{i-1}x^i}{i}\)
正常推导法:
\(\ln(1+x)'=\frac{1}{1+x}=\sum_i (-1)^ix^i\)
\(\int(\ln(1+x)')=\ln(1+x)=\sum_i \frac{(-1)^ix^{i+1}}{i+1}=\sum_{i>=1}\frac{(-1)^{i-1}x^i}{i}\)
我是傻逼
那么可以搞一开始的式子了,代入-x^i:
\(\ln Ans(x)=-\sum_{i>=1}\ln(1-x^i)\)
\(=-\sum_{i>=1}\sum_{j>=1}\frac{(-1)^{2j-1}x^{ij}}{j}=\sum_{i>=1}\sum_{j>=1}\frac{x^{ij}}{j}\)
要求的是\(x^{n+1}\)意义下的多项式,所以ij<=n,暴力枚举即可处理出\(\ln Ans(x)\),取exp还原
PS:
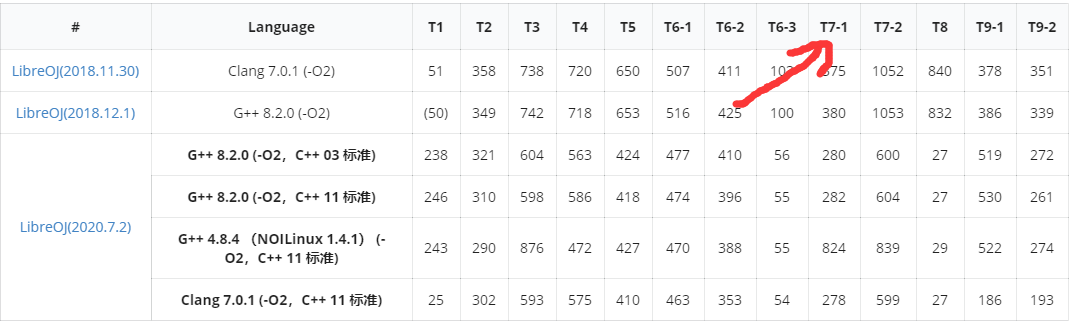

所以如果用了NOI编译器会被T成sb
code
loj6268
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
#define Mod 998244351
#define G 114514
#define ll long long
//#define file
using namespace std;
ll a[262144],ans[262144],ww[262144],w[19][262144],W[19][262144];
int a2[19][262144],N,len,n,i,j,k,l;
char st[21],ch;
void Write(int x) {int i=0; if (!x) {printf("0\n");return;} while (x) st[++i]=x%10+'0',x/=10; while (i) putchar(st[i--]);putchar('\n');}
ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
void dft(ll *a,int tp,int N,int len)
{
static ll A[262144];
int i,j,k,l,S=N,s1=2,s2=1;
ll u,v;
fo(i,0,N-1) A[i]=a[a2[len][i]];
memcpy(a,A,N*8);
fo(i,1,len)
{
S>>=1;
fo(j,0,S-1)
{
fo(k,0,s2-1)
{
u=a[j*s1+k],v=a[j*s1+k+s2]*(tp==1?w[i][k]:W[i][k]);
a[j*s1+k]=(u+v)%mod;
a[j*s1+k+s2]=(u-v)%mod;
}
}
s1<<=1,s2<<=1;
}
}
void mul(ll *a,ll *b,ll *c,int N,int len)
{
static ll A[262144],B[262144];
int i,j,k,l,N2=qpower(N,Mod);
memcpy(A,a,N*8),memcpy(B,b,N*8);
dft(A,1,N,len),dft(B,1,N,len);
fo(i,0,N-1) A[i]=A[i]*B[i]%mod;
dft(A,-1,N,len);
fo(i,0,N-1) c[i]=A[i]*N2%mod;
}
void ny(ll *a,ll *b,int N,int len)
{
static ll A[262144],B[262144];
int i,j,k,l;
if (N==1) {b[0]=qpower(a[0],Mod);return;}
ny(a,b,N/2,len-1);
memset(A,0,N*2*8),memset(B,0,N*2*8);
mul(b,b,A,N,len);
memcpy(B,a,N*8);
mul(A,B,A,N*2,len+1);
fo(i,0,N-1) b[i]=(2*b[i]-A[i])%mod;
}
void dao(ll *a,int N,int len)
{
int i,j,k,l;
fo(i,0,N-2) a[i]=a[i+1]*(i+1)%mod;a[N-1]=0;
}
void ji(ll *a,int N,int len)
{
int i,j,k,l;
fd(i,N-1,1) a[i]=a[i-1]*ww[i]%mod;a[0]=0;
}
void Ln(ll *a,ll *b,int N,int len)
{
static ll A[262144],B[262144];
int i,j,k,l;
memset(A,0,N*2*8);memset(B,0,N*2*8);
memcpy(A,a,N*8),dao(A,N,len);
ny(a,B,N,len);
mul(A,B,B,N*2,len+1);
memcpy(b,B,N*8),ji(b,N,len);
}
void Exp(ll *a,ll *b,int N,int len)
{
static ll A[262144],B[262144];
int i,j,k,l;
if (N==1) {b[0]=1;return;}
Exp(a,b,N/2,len-1);
memset(B,0,N*2*8);Ln(b,B,N,len);
fo(i,0,N-1) B[i]=(a[i]-B[i])%mod;++B[0];
memset(A,0,N*2*8);memcpy(A,b,N*4);
mul(A,B,B,N*2,len+1);
memcpy(b,B,N*8);
}
void init()
{
ww[1]=1;
fo(i,2,262143) ww[i]=mod-ww[mod%i]*(mod/i)%mod;
N=1;
fo(len,1,18)
{
N<<=1;
w[len][0]=W[len][0]=1;
w[len][1]=qpower(G,(mod-1)/N),W[len][1]=qpower(G,(mod-1)-(mod-1)/N);
fo(i,2,N-1) w[len][i]=w[len][i-1]*w[len][1]%mod,W[len][i]=W[len][i-1]*W[len][1]%mod;
fo(i,0,N-1)
{
j=i,k=0;
fo(l,1,len)
k=k*2+(j&1),j>>=1;
a2[len][i]=k;
}
}
}
int main()
{
#ifdef file
freopen("loj6268.in","r",stdin);
freopen("a.out","w",stdout);
#endif
init();
scanf("%d",&n);len=ceil(log2(n+1)),N=qpower(2,len);
fo(i,1,n)
{
for (j=i; j<=n; j+=i)
a[j]=(a[j]+ww[j/i])%mod;
}
Exp(a,ans,N,len);
fo(i,1,n) Write((ans[i]+mod)%mod);
fclose(stdin);
fclose(stdout);
return 0;
}

