多项式小结（求逆、求导、积分、ln、牛顿迭代、exp）
求逆
求\(A(x)B(x)\equiv 1(mod\;x^n)\)，下文为了方便表述把n/2
已知\(A(x)C(x)\equiv 1(mod\;x^n)\)，倍增求\(A(x)B(x)\equiv 1(mod\;x^{2n})\)，下文为了方便把(x)省掉
\(A(B-C)\equiv 0(mod\;x^n)\)
\(A^2(B-C)^2\equiv 0(mod\;x^{2n})\)
\(A(B-C)^2\equiv 0(mod\;x^{2n})\)
\(AB^2-2ABC+AC^2\equiv 0(mod\;x^{2n})\)
\(B-2C+AC^2\equiv 0(mod\;x^{2n})\)
\(B\equiv 2C-AC^2(mod\;x^{2n})\)
求导
求\(A'(x)\)，本质是求一点的斜率，定义\(A_i=A(x)[x^i]\)
\(A'(x)=\frac{\sum A_i((x+\Delta)^i-x^i}{\Delta}\)
当\(\Delta\rightarrow0\)时\(A'(x)=\sum_{i>=1} iA_ix^{i-1}\)
复合函数求导
\(G(x)=F(A(x)),G'(x)=F'(A(x))A'(x)\)
这个的意义是以x为自变量的导，而\(F'(A(x))\)的意义是以A(x)为自变量的导
所以ln中求的是G'(x)，牛顿迭代把A当作自变量求的是F'(A(x))
积分
是不定积分，即求导的逆运算
\(\int A(x)=\sum_{i>=1} \frac{1}{i}x^iB_{i-1}\)
积分后再求导常数项会消失
ln
求\(G(x)=ln(F(x))\)，具体的意义是什么并不是很知道
复合函数求导：\(G(x)=F(A(x))\)，\(G'(x)=F'(A(x))A'(x)\)，并且有\(ln'(x)=\frac{1}{x}\)
\(G'(x)=\frac{F'(x)}{F(x)}\)
\(G(x)=\int \frac{F'(x)}{F(x)}\)
牛顿迭代
对于普通的多项式\(A(x)\)求零点x，设上一次求得的是x0（不一定是零点）
在\((x0,f(x0))\)处做切线，斜率为\(f'(x0)\)，则根据简单三角函数有
\(\frac{f(x0)}{x0-x}=f'(x0)\)
\(x=x0-\frac{f(x0)}{f'(x0)}\)
牛顿迭代求的是近似解，但
exp
先不考虑精度，求\(B(x)=e^{A(x)}(mod\;x^n)\)
\(ln(B(x))=A(x)(mod\;x^n)\)
\(ln(B(x))-A(x)=0(mod\;x^n)\)
把B当作变量，A当作常数并不知道为什么可以这样
设\(F(B(x))=ln(B(x))-A(x)\)，则\(F'(B(x))=\frac{1}{B(x)}\)（函数相加的导数=分别的导数和，A看作常数了所以是0）
把n/2，代牛顿迭代的式子，设\(C(x)\)是模\(x^n\)下的解，求模\(x^{2n}\)下的解\(B(x)\)
\(B(x)=C(x)-C(x)(ln(C(x))-A(x))(mod\;x^{2n})\)
\(B(x)=C(x)(1-ln(C(x))+A(x))(mod\;x^{2n})\)
正确性证明
泰勒展开：
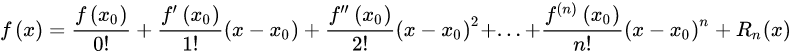
x即\(B(x)\)，x0即\(C(x)\)，相减之后前n项是0，平方之后前2n项是0，于是被模掉了（
所以只剩前两项了，根据牛顿迭代的定义
发现取的就是前两项，现在只剩前两项了，所以是精确解（
其实模完之后变成了一条直线，所以可以求解
n^2lnexp
模数不是ntt模数时可以用，也有学的必要
https://www.cnblogs.com/gmh77/p/13162153.html
exp
设\(g(x)=e^{f(x)}\)，设\(g_n\)为\(g(x)[x^n]\)，\(f_n\)为\(f(x)[x^n]\)
\(g(x)=e^{f(x)}\)
\(g'(x)=e^{f(x)}f'(x)\)
因为\(f'(x)=\sum{i*x^{i-1}f_i}\)
所以\(xf'(x)=\sum_{i>=1}{i*x^if_i}\)
\(ng_n=\sum_{i=0}^{n}{g_{n-i}if_i}\)
硬点g0=1，然后即可n^2求得exp
原因是f(x)没有常数项（否则求不出来），所以\(e^x\)展开后只有\(\frac{x^0}{0!}=1\)
ln
\(ng_n=\sum_{i=0}^{n-1}{g_{n-i}if_i}+nf_n\)
\(nf_n=ng_n-\sum_{i=0}^{n-1}{g_{n-i}if_i}\)
快速幂
先ln，乘上系数后exp
lnexp来搞是线性卷积，dft再乘k是循环卷积
时间复杂度
上面的那一坨都是nlogn的，但是常数略大
调试方法&注意事项
一定要把不用的位置清空，相乘长度开到长度和
两个长度为N的多项式相乘时一定要把[N,2N-1]清空
调试小技♂巧：
快速幂->exp->ln->求导积分求逆->NTT，从后往前调试
要测小数据和中数据，多测几遍+改n和len看有没有变
ln再exp和exp再ln结果不变，可以利用这点来查错
可以在不用的位上加一些数看答案是否会改变
exp的组合意义：\(e^x=\sum \frac{x^i}{i!}\)，所以可以手玩判断exp是否写对
如果exp对了而ln+exp/exp+ln错了那就是数组没有清空
例题
6712.【2020.06.09省选模拟】题3
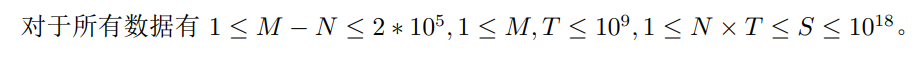
题解
推式子省略，变成快速幂
code
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define C(n,m) (jc[n]*Jc[m]%998244353*Jc[(n)-(m)]%998244353)
#define mod 998244353
#define Mod 998244351
#define G 3
#define ll long long
#define file
using namespace std;
ll A2[524288],a[524288],b[524288],c[524288],w[524288],S,T,n,m,s;
int a2[20][524288],i,j,k,l,N,len;
ll qpower(ll a,int b) {ll ans=1; while (b) {if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;} return ans;}
//static ll a[maxn];
void dft(ll *a,int tp,int N,int len)
{
int i,j,k,l,S=N,s1=2,s2=1;
ll u,v,w,W;
fo(i,0,N-1) A2[i]=a[a2[len][i]];
memcpy(a,A2,N*8);
fo(i,1,len)
{
W=(tp==1)?qpower(G,(mod-1)/s1):qpower(G,(mod-1)-(mod-1)/s1);S>>=1;
fo(j,0,S-1)
{
w=1;
fo(k,0,s2-1)
{
u=a[j*s1+k],v=a[j*s1+k+s2]*w;
a[j*s1+k]=(u+v)%mod;
a[j*s1+k+s2]=(u-v)%mod;
w=w*W%mod;
}
}
s1<<=1,s2<<=1;
}
}
namespace Mul{ll a[524288],b[524288];}
void mul(ll *a,ll *b,ll *c,int N,int len)
{
ll N2=qpower(N,Mod);
int i,j,k,l;
memcpy(Mul::a,a,N*8),memcpy(Mul::b,b,N*8);
dft(Mul::a,1,N,len);dft(Mul::b,1,N,len);
fo(i,0,N-1) c[i]=Mul::a[i]*Mul::b[i]%mod;
dft(c,-1,N,len);
fo(i,0,N-1) c[i]=c[i]*N2%mod;
}
namespace Ny{ll a[524288],b[524288];}
void ny(ll *a,ll *b,int N,int len)
{
int i,j,k,l;
memset(b,0,N*8);
if (N==1) {b[0]=qpower(a[0],Mod); return;}
ny(a,b,N/2,len-1);
memset(Ny::a,0,N*16);
mul(b,b,Ny::a,N,len);
memset(Ny::b,0,N*16);
fo(i,0,N-1) Ny::b[i]=a[i];
mul(Ny::a,Ny::b,Ny::a,N*2,len+1);
fo(i,0,N-1) b[i]=(b[i]*2-Ny::a[i])%mod;
}
void dao(ll *a,int N)
{
int i;
fo(i,0,N-2) a[i]=a[i+1]*(i+1)%mod;a[N-1]=0;
}
void ji(ll *a,int N)
{
int i;
fd(i,N-1,1) a[i]=a[i-1]*w[i]%mod;a[0]=0;
}
namespace LN{ll a[524288];}
void Ln(ll *a,int N,int len)
{
int i;
memset(LN::a,0,N*16);memcpy(LN::a,a,N*8);
ny(LN::a,a,N,len);dao(LN::a,N);
mul(a,LN::a,a,N*2,len+1);
ji(a,N);fo(i,N,N+N-1) a[i]=0;
}
namespace EXP{ll a[524288];}
void Exp(ll *a,ll *b,int N,int len)
{
int i,j,k,l;
memset(b,0,N*8);
if (N==1) {b[0]=1;return;}
Exp(a,b,N/2,len-1);
memset(EXP::a,0,N*8);memcpy(EXP::a,b,N*4);
Ln(EXP::a,N,len);
fo(i,0,N-1) EXP::a[i]=(-EXP::a[i]+a[i])%mod;++EXP::a[0];fo(i,N,N+N-1) EXP::a[i]=0;
mul(b,EXP::a,b,N*2,len+1);fo(i,N,N+N-1) b[i]=0;
}
namespace Mi{ll a[524288];}
void mi(ll *a,ll k,int N,int len)
{
ll s=qpower(a[0],k);
int i;
memcpy(Mi::a,a,N*8);
Ln(Mi::a,N,len);
fo(i,0,N-1) Mi::a[i]=Mi::a[i]*(k%mod)%mod;
Exp(Mi::a,a,N,len);
fo(i,0,N-1) a[i]=a[i]*s%mod;
}
void init()
{
int I,s=1;
w[1]=1;
fo(i,2,200000) w[i]=mod-w[mod%i]*(mod/i)%mod;
fo(I,0,19)
{
fo(i,0,s-1)
{
j=i;k=0;
fo(l,1,I) k=k*2+(j&1),j>>=1;
a2[I][i]=k;
}
s*=2;
}
}
void work()
{
s=1;fo(i,1,m-n+1) s=s*((T-i+1)%mod)%mod*w[i]%mod,a[i-1]=s;
s=1;fo(i,0,m-n) b[i]=s,s=s*(((S-n*T)-(i+1)+1)%mod)%mod*w[i+1]%mod;
mi(a,n,N,len);
mul(a,b,a,N*2,len+1);
}
int main()
{
freopen("sum.in","r",stdin);
#ifdef file
freopen("sum.out","w",stdout);
#endif
scanf("%lld%lld%lld%lld",&S,&T,&n,&m);len=ceil(log2(m-n+1));N=qpower(2,len);
init();
work();
printf("%lld\n",(a[m-n]+mod)%mod);
fclose(stdin);
fclose(stdout);
return 0;
}
