arc109D - L/arc109E - 1D Reversi Builder/arc109F - 1D Kingdom Builder

D - L

题目大意：

3个石子，初始在(0,0)(0,1)(1,0)，每次可以把一个石子移到任意位置，满足移动后仍然是类似初始的L形，求移到给定位置的最小步数（石子之间完全相同）

T<=1e3,|x|,|y|<=1e9

题解：

有114514种写法，但是大多很难写

CF上一位老鸽的做法：找出L形所在的2*2矩形，将其缩到矩形的左下角，则新格子中有四个点对应L的四种形态，每次可以往九个方向移动，但不能穿过格子的交点

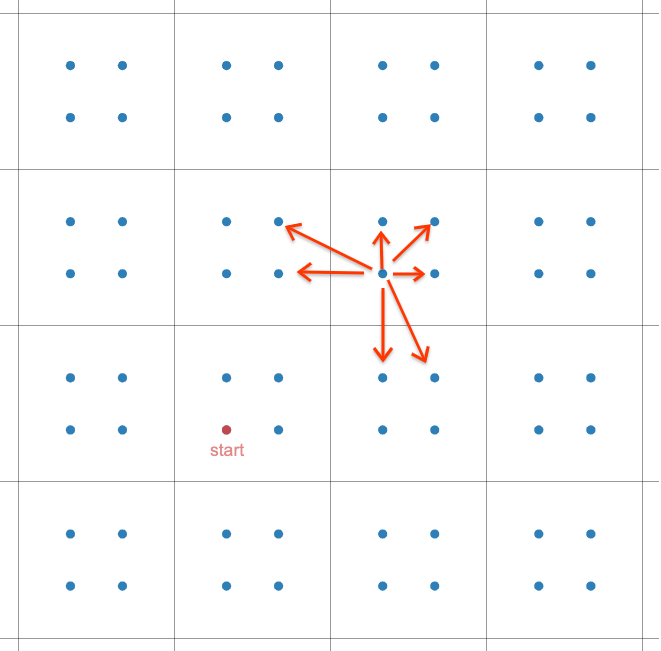
转化之后判一下是否在y=x上且不在初始格子里，然后取max(x,y)即可

E - 1D Reversi Builder

题目大意：https://www.cnblogs.com/jz-597/p/14058486.html

题解：

考场一开始在想n^3暴力，后来换了一下直接枚举ij阳间n^2，接着发现可以直接枚举分界点然后前缀和，最后10min过了

简单的结论：黑白双方都会径直超边界处和自己颜色相同的块走去

如果边界同色则显然一方怎么走都不行，否则可以发现在中间走没有意义，因为最终中间的段取决于最靠两边的两块相同颜色的（一块靠边界，一块靠另一方靠边界的块），如果抢到了自己那边靠边界的，则对方迟早会走到另一块然后把中间变成自己的

枚举ij，在(i+j)/2处前后缀和即可n^2，实际上发现贡献和ij大小有关且单调递增，所以把l从1到n扫，同时维护区间变化以及乘上i或j的和

当然还可以把最后答案差分oeis

F - 1D Kingdom Builder

题目大意：一排黑白格子，给出[1,n]内的格子颜色，<=0的全白>n的全黑

现在在格子上放石头，每次选择一种颜色然后考虑之前放下的所有石头，如果有某个颜色和选择颜色相同且相邻有石头的空格子，则在这些空格子里选一个放，否则在任意一个和选择颜色相同的格子上放

求放完后使得一些给出位置上都有石头所需要的最小石头数，n<=1e5

题解：

对于arc来说挺阴间的

首先考虑判断合法，设最后一段第一个放的颜色为c，考虑把操作反过来变成删石子，每次删掉一个任意位置的，如果某一段只有那一个就要满足剩余的段两侧（段外相邻的）没有和其颜色相同的

那么显然先删最后一段，删剩c的时候考虑把其他段删成一段满足两侧都不是c的子串，接着把最后一段删掉

然后考虑贪心，由于现在两侧没有c了，所以如果某段中间有c则可以直接将其整段删掉，这样删下去最后会剩下全部为c反色的段，此时如果有大于1段则显然不能删，否则剩下的这段就是第一段

整理一下，就是这样两条限制：

①每段都要有长度>=1的子串s，满足其两侧都不为c（除最后一段）

②子串s内部要有c（除第一段）

于是对于普通段来说，其状态可以分成不选/选/选了一个≠c/又选了一个c/再选了一个≠c，加上第一段和最后一段是否选，可以记f[i,0/1/2/3/4,0/1,0/1]的dp转移

对于第一段和最后一段就特殊考虑，第一段内部无c所以可以在遇到第二个≠c时成段，最后一段没有两侧限制所以可以在遇到第一个c时成段

转移考虑做完了[0,i]，考虑加上i+1后的影响（i+1作为右侧），如果选就再考虑i作为左侧的影响，注意转移时子串s不能为空，尤其是两种特殊情况

时间O(n)

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define Min(a,b) a=(min((a),(b)))
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
#define inf 2000000000
#define ll long long
//#define file
using namespace std;

int n,i,j,k,l,J,ans=2147483647;
int f[100012][5][2][2];
char a[100012],b[100012];

void work(char ch)
{
	memset(f,127,sizeof(f));
	f[0][0][0][0]=0;
	fo(i,0,n)
	{
		fo(j,0,4)
		{
			fo(k,0,1)
			{
				fo(l,0,1)
				if (f[i][j][k][l]<inf)
				{
					if (b[i+1]!='o')
					{
						if (!j)
						Min(f[i+1][0][k][l],f[i][0][k][l]);
						if (!k)
						{
							if (j>=2 && j<=3 && a[i+1]!=ch)
							Min(f[i+1][0][1][l],f[i][j][k][l]);
						}
						if (j==3 && a[i+1]!=ch || j==4)
						Min(f[i+1][0][k][l],f[i][j][k][l]);
					}
					
					J=max(j,1);
					if (J==1 && a[i]!=ch) J=2;
					if (J==2 && a[i+1]==ch) J=3;
					if (J==3 && a[i+1]!=ch) J=4;
					Min(f[i+1][J][k][l],f[i][j][k][l]+1);
					if (!k)
					{
						J=max(j,1);
						if (J==1 && a[i]!=ch) J=2;
						if (J==2 && a[i+1]==ch) J=3;
						if (j>=2 && J>=2 && J<=3 && a[i+1]!=ch) J=4;
						Min(f[i+1][J][1][l],f[i][j][k][l]+1);
					}
					if (!l)
					{
						J=max(j,1);
						if (J==1 && a[i]!=ch) J=2;
						if (J<=3 && a[i+1]==ch) J=4;
						if (J==3 && a[i+1]!=ch) J=4;
						Min(f[i+1][J][k][1],f[i][j][k][l]+1);
					}
				}
			}
		}
	}
	fo(j,0,4) if (!j || j==4) {fo(k,0,1) fo(l,0,1) ans=min(ans,f[n+1][j][k][l]);}
}

int main()
{
	#ifdef file
	freopen("arc109F.in","r",stdin);
	#endif
	
	scanf("%d",&n);
	scanf("%s",a+1),scanf("%s",b+1);
	k=l=0;
	fo(i,1,n) if (b[i]=='o') k=(!k)?i:k,l=i;
	ans=l-k+1;
	a[0]='w';++n;fd(i,n,2) a[i]=a[i-1],b[i]=b[i-1];
	a[1]='w',b[1]='_',a[++n]='b',a[n+1]='b';
	
	work('w'),work('b');
	printf("%d\n",ans);
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}