ARC061F - Card Game for Three

可以发现当把出牌顺序看成一个序列， 每个序列对应的就是一种局面

例如"bc"我们可以当成a先打了一张b， 然后b打了一张c， 然后轮到c结束了（因为是a先开始）

转换出来之后我们就可以把问题抽象成， 有多少个序列， 其存在一个前缀， 满足这个前缀包含n个a， 不超过m个b， 不超过k个c

那么， 容易发现最短的前缀他一定是以a结尾的， 那么， 我们通过枚举前缀长度， 可以得到一个显然的$O(N^2)$做法

$$ans = \sum_{i=0}^m \sum_{j=0}^k C(n+i+j-1, i)C(n+j-1, j)3^{m+k-i-j}$$

其中i表示b的个数， j表示c的个数， 当满足这个前缀之后， 后面的出牌顺序和牌的种类已经不重要了， 所以后面有$3^{m+k-i-j}$

 

现在考虑优化这个式子

给这个式子变化一下形式

 

$=\sum_{i=0}^m \sum_{j=0}^k C(n+i+j-1, i)C(n+j-1, j)3^{m+k-i-j} \\  = \sum_{i=0}^m \sum_{j=0}^k \frac{(n+i+j-1)!}{i!(n+j-1)!} \frac{(n+j-1)!}{j!(n-1)!}3^{m+k-i-j}\\  = \sum_{i=0}^m \sum_{j=0}^k \frac{(n+i+j-1)!}{(n-1)!(i+j)!} \frac{(i+j)!}{j!i!}3^{m+k-i-j} \\ =\sum_{i=0}^m \sum_{j=0}^k C(n+i+j-1, n-1) C(i+j, j) 3^{m+k-j-i} \\ = \sum_{i=0}^{m+k} \sum_{j=max(i-m, 0)}^{min(i, k)} C(n+i-1, n-1) C(i, j) 3^{m+k-i}\\ = \sum_{i=0}^{m+k}C(n+i-1, n-1)3^{m+k-i} \sum_{j=max(i-m, 0)}^{min(i, k)}  C(i, j)$

 

其实上式已经分离了两个变量， 我们只需要解决如何快速的求后面这个东西， 即$\sum_{j=max(i-m, 0)}^{min(i, k)}  C(i, j)$

然后我们发现两个界限 $max(i-m, 0)\leq j\leq min(i, k)$

 

也就是说我们可以分成三段

第一段， i <= k, 此时 $\sum_{0}^{i}  C(i, j)=2^i$

第二段， 当i>k， 此时$\sum_{j=0}^{k}  C(i, j)$是一个组合数前k项和的形式， 这个东西可以用一个线性递推来解决， 设$f[i]$表示组合数i的前k项和， 那么有$f[i] = 2f[i-1] - C(i-1, k)$

具体解释如图：

那么$f[i] - 1= 2f[i-1] - C(i-1, k) - C(i-1, 0)$

 

因为$C(i,j) = C(i-1, j) + C(i-1, j-1)$

第三段， 当i>m，上面两个加多了的东西得减掉， 也就是$\sum_{j=0}^{i-m-1} C(i, j)$， 这个东西同样可以用一个线性递推来解决， 设$g[i]$表示前$i-m-1$项和， 因为$i-m-1$肯定不会超过k， 所以当i+1的时候j也在+1， 如图

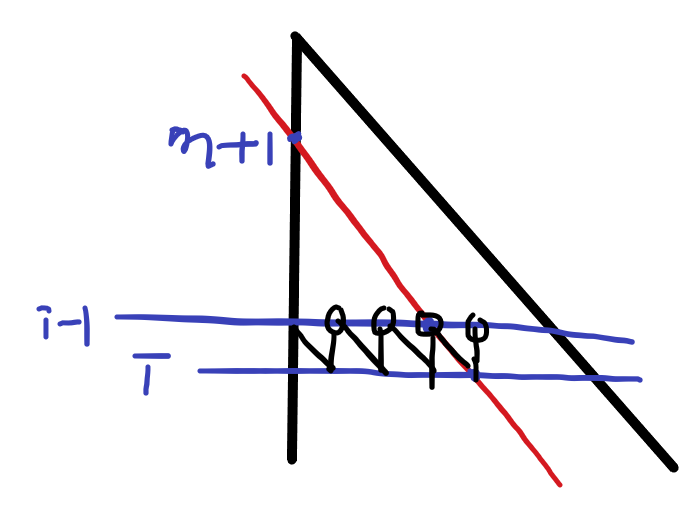那么$g[i] -1  = 2g[i-1] + C(i-1, i-m-1) - C(i-1, 0)$ 因为不论是上面还是下面， 0都只会被记一次， 而下面这个式子里， 我们需要补一个$C(i-1, i-m-1)$来组成$C(i, i-m-1)$

 

最后只需要把前两段加起来然后减去第三段的东西就可以了

 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
#define pb push_back
#define ln '\n'
const int N = 9e5+5;
const int mod = 1e9+7;
inline void inc(int &a, int b){
    a+=b;
    if(a>=mod) a-=mod;
}
inline void dec(int &a, int b){
    a-=b;
    if(a<0) a+=mod;
}
inline int power(int a, int b){
	int res = 1;
	for(; b; b >>= 1, a=1ll*a*a%mod)
		if(b&1)
			res=1ll*res*a%mod;
	return res;
}
int fac[N], inv[N], f[N], g[N];
inline void prework(int n){
	fac[0] = 1;
	for(int i = 1; i <= n; i++)
		fac[i] = 1ll * fac[i-1] * i % mod;
	inv[n] = power(fac[n], mod-2);
	for(int i = n; i; i--)
		inv[i-1] = 1ll * inv[i] * i % mod;
}
inline int C(int n, int m){
	return 1ll * fac[n] * inv[m] % mod * inv[n-m] % mod;
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n, m, k;
    cin >> n >> m >> k;
    prework(n+m+k);
    int ans = 0;
    for(int i = 0; i <= k; i++)
    	inc(ans, 1ll*C(n+i-1, n-1)*power(3, m+k-i)%mod*power(2, i)%mod);
    f[k] = power(2, k);
    for(int i = k + 1; i <= m+k; i++){
    	f[i] = (2*f[i-1]%mod - C(i-1, k) + mod) % mod;
    	inc(ans, 1ll*C(n+i-1, n-1)*power(3, m+k-i)%mod*f[i] % mod);
    }

    g[m] = 0;
    for(int i = m+1; i <= m+k; i++){
    	g[i] = (2*g[i-1]%mod + C(i-1, i-m-1)) % mod;
    	dec(ans, 1ll*C(n+i-1, n-1)*power(3, m+k-i)%mod*g[i] % mod);
    }
    cout << ans << ln;
}