20172301 《程序设计与数据结构》第八周学习总结

20172301 《程序设计与数据结构》第八周学习总结

教材学习内容总结

堆

• 堆：是具有两个附加属性的一棵二叉树。

  • 是一棵完全树。
  • 最小堆对每一结点，它小于或等于其左孩子和右孩子。反之，最大堆对每一个结点大于或等于它的左右孩子。
  • ，最小堆将其最小元素存储在该二叉树的根处，且最小堆根结点的子树同样也是最小堆。
    

• addElement操作：将给定的元素添加到堆中的恰当位置，维持该堆的完全性属性和有序属性。

  • 如果元素不是Comparable类型的，则会抛出异常。这是为了让元素可比较，可以维持堆的有序属性。
  • 而为了维护堆的完全性，就决定了堆插入结点时只有两种情况：

  1.h层的左边下一个位置。
  2.h+1层的第一个位置。（h层为满）

  • 将新元素添加到堆的末尾后，考虑到有序属性，将该元素与父结点进行比较，若小将它与父结点对换，直到大于父结点或者位于根结点处。

• removeMin操作：删除堆的最小元素：删除堆的最小元素并且返回。

  • 最小元素位于根结点，删除掉根结点，为了维持树的完全性，要找一个元素来替代它，那么只有一个能替换根的合法元素，且它是存储在树中最末一片叶子上的元素。最末的叶子是h层上最右边的叶子。
  • 考虑到有序属性，对该堆重新排序。将新的根元素和其较小的孩子比较，如果孩子更小，那么他们互换，直到该元素位于某个叶子中或者比他的两个孩子都小。

• findMin操作：指向最小堆的最小元素。

  • 返回存在根处的元素。

用链表实现堆

• 因为要求插入元素以后能够向上遍历，所以堆中的结点必须存储指向双亲的指针。继承BinaryTreeNode类，并且添加双亲指针和对应的set方法。

• 有一个实例数据lastNode作用是跟踪记录堆中的最后一个叶子，也就是指向末结点的引用。
  

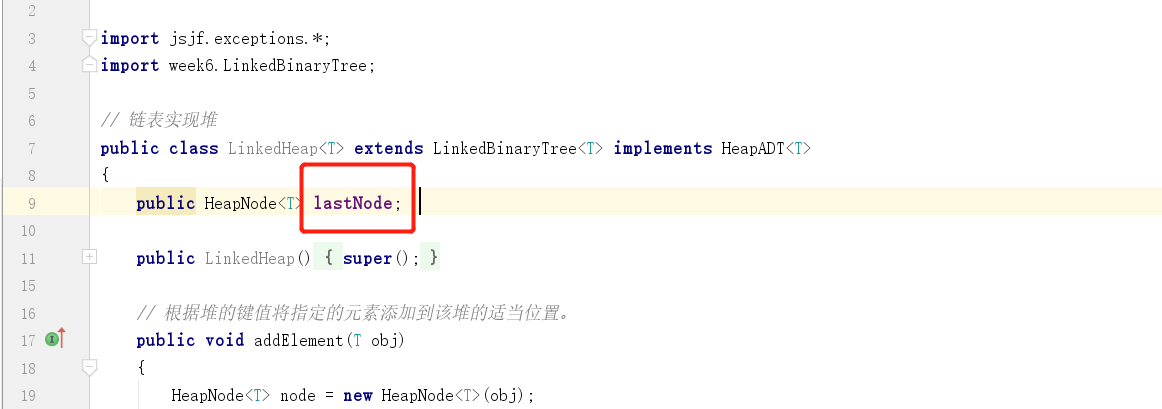
• addElement操作：

  • 在适当位置添加一个元素。
  • 对堆进行重排序，以保持其有序属性。
  • 将lastNode指针重新设定为指向新的最末结点。
  • 在最坏的情况下，确定要插入结点的双亲，需要从堆的右下结点往上遍历到根，然后往下遍历到堆的左下结点。时间复杂度为2 * logn。插入新结点，简单赋值，时间复杂度为O(1)。如果需要重排序，最多需要比较logn次，因为路径最长为logn。所以addElement操作的复杂度为2 * logn + 1 + logn，为O(logn)。

• removeMin操作：

  • 用存储在最末结点处的元素替换存储在根处的元素。
  • 对堆进行重排序。
  • 返回原来的根元素。
  • 在最坏的情况下，替换结点，简单赋值，时间复杂度为O(1)，然后重排序，，因为路径最长为logn，所以还是比较logn次。确定新的最末结点，从叶子到根的遍历，再从根到另一个叶子的遍历。所以removeMin操作的复杂度为2 * logn + logn + 1，为O(logn)。

• findMin操作

  • 直接返回根元素，复杂度为O(1)。

用数组实现堆

• 树的根位于位置0处，对于每一结点n，n的左孩子将位于数组的2n+1位置处，n的右孩子将位于数组的2（n+1）位置处。
• addElement操作：
  • 在恰当位置处添加新结点。
  • 对堆进行重排序以维持其排序属性。
  • 将count值递增1。
  • 时间复杂度为 1 + log ，为 O(logn)。
• removeMin操作
  • 用存储在最末元素处的元素替换存储在根处的元素。
  • 对堆进行重排序。
  • 返回初始的根元素，并将count值减1。
  • 时间复杂度为 1 + log ，为 O(logn)。
• findMin操作
  • 指向索引为0，时间复杂度为O(1)。

使用堆：优先级队列

• 遵循两个排序规则：
  • 具有更高优先级的项目在先。
  • 具有相同优先级的项目使用先进先出方法来确定顺序。
• 虽然最小堆根本就不是一个队列，但是它却提供了一个高效的优先级队列实现。

使用堆：堆排序

• 原理：根据堆的有序属性，将列表的每一个元素添加到堆中，然后一次一个的把他们从根中删除。
• 堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)。
• 堆排序时间复杂度O(nlogn)。
• 步骤：
  • 步骤一：构造初始堆。将给定无序序列构造成一个堆（升序采用小顶堆，降序采用大顶堆)。
  • 步骤二：将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

教材学习中的问题和解决过程

• 问题1：链表堆和数组堆的优缺点。

• 问题1解决方案：

  • 在之前章节的树的实现中，我们大多数用的都是链表实现的。主要是因为，用数组实现树的时候，可能会因为没有左右孩子而浪费了大量的空间。但是，在堆的实现中，因为考虑其向上遍历的特殊操作，我们需要其双亲结点 。而又因为堆是一个完全树，所以，不会存在大量浪费空间的情况 。所以，针对堆来说，数组实现的效率更高。
  • 根据书P268 和 P270，

  因为数组不需要确定新结点双亲的步骤，以及数组不需要确定新的最末结点。所以，虽然他的时间复杂度和用链表实现时是一样的，但是数组实现的效率更高一些。

  • 同样，我们不必拘泥于一种结构，一种实现方式。平常编写代码时也要注意其效率，代码的相关优化和美观。不要只把实现和完成任务当成标准。这是我以后也应该注意的。

• 问题2：对于课上将的堆排序，还有课上的堆排序实践没有熟练掌握。重点归纳记忆一下。

• 问题2解决方案：

  • 首先，要清楚堆排序的思想，堆排序是一种选择排序 。如何将一个杂乱排序的堆重新构造成最大堆，它的主要思路就是

  从上往下，将父节点与子节点以此比较。如果父节点最大则进行下一步循环，如果子节点更大，则将子节点与父节点位置互换，并进行下一步循环。注意父节点要与两个子节点都进行比较。

  • 我们第一步就应该明白，如何将一个无序列表构建成最大堆。

  从最后一个非叶节点开始调整。

  

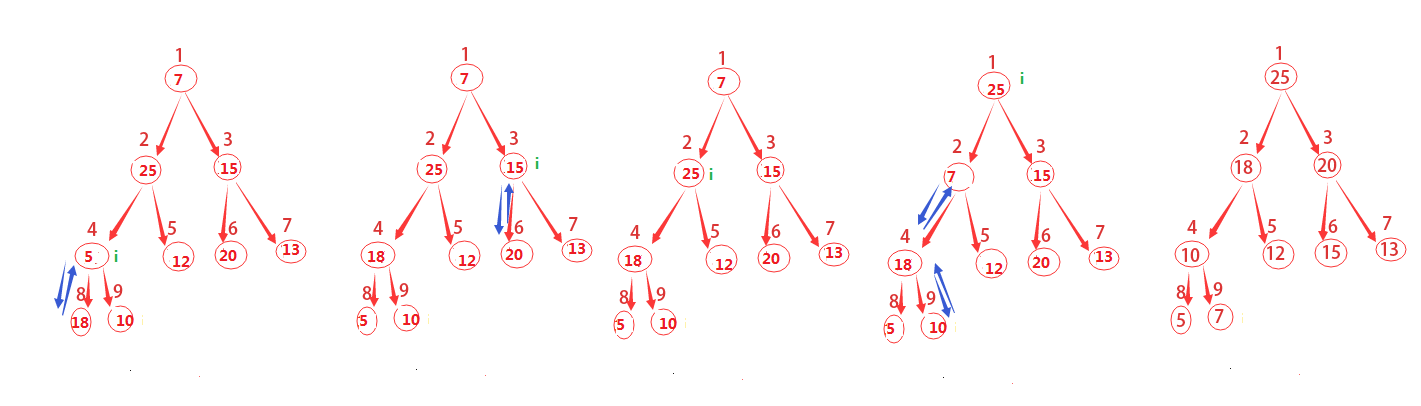
  • 如图，这里的最后一个非叶子结点是结点4，那么我们就从这里进行调整。

  每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。

  

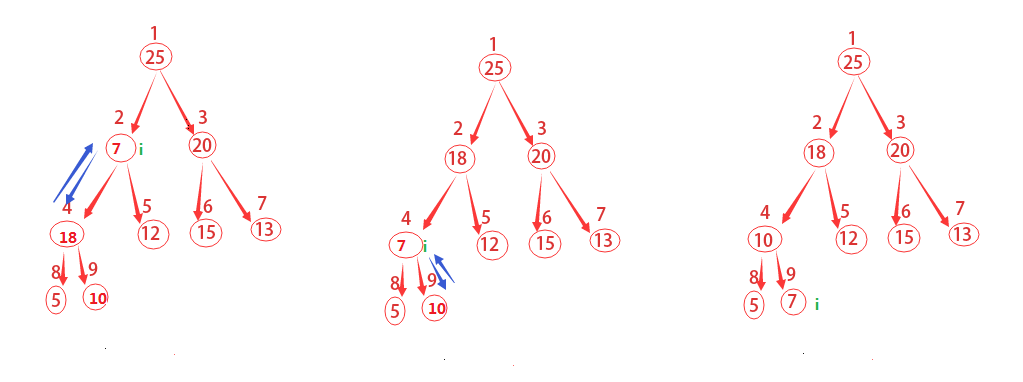
  • 如上图，这里从结点2开始做调整。左孩子为结点4，右孩子为结点5，将其与父结点做比较，发现左孩子比父结点更大。因此将它们做交换，设结点4为最大的结点，并继续以结点4开始做下一步运算。
  • 当构建好一个堆之后，我们开始进行排序。将堆顶元素与末尾元素进行交换，使末尾元素最大。然后重新调整堆，一直到最后整个堆都不存在了，那么数组就是有序的。
    

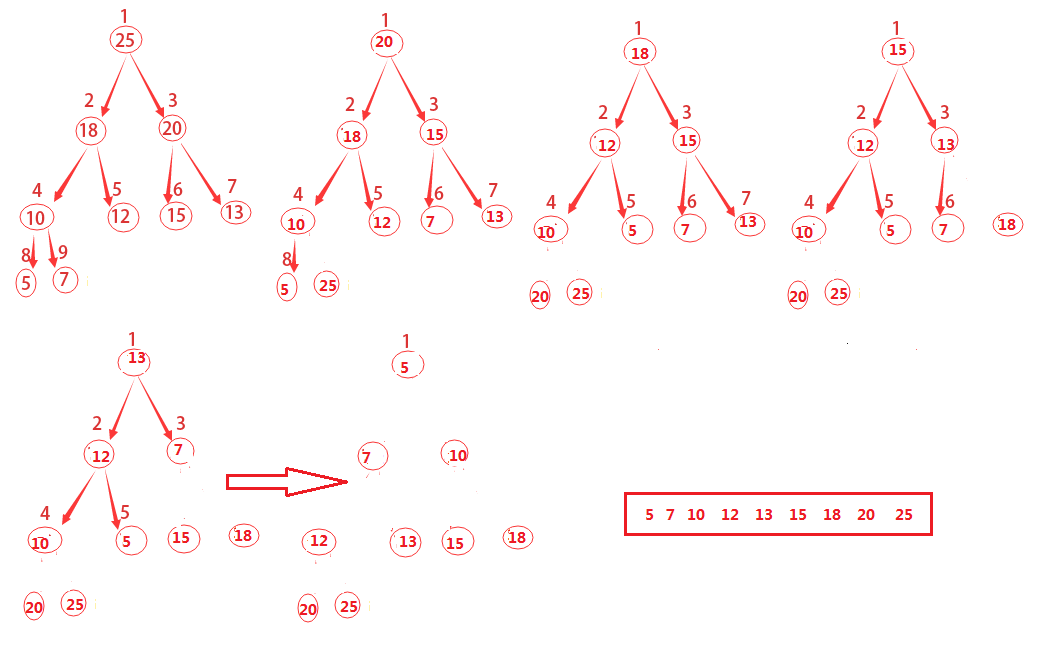
代码调试中的问题和解决过程

• 问题1：在实现PP12.1的时候，发现使用remove操作之后，虽然删除了第一个进入的元素，但是又添加了一个元素。
  

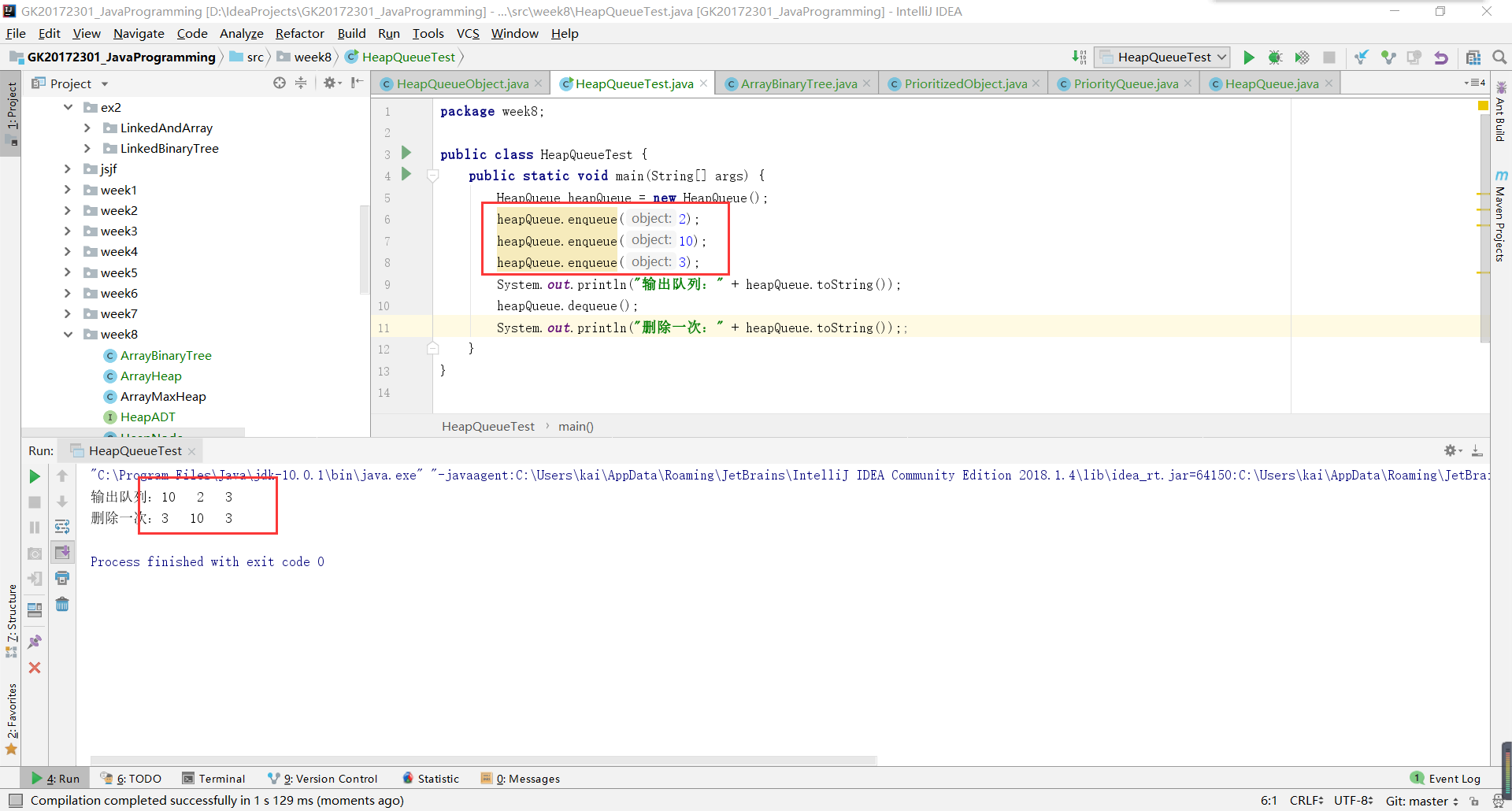
如图，发现，我插入队列的依次是，2，10，3。然后中序遍历就是10，2，3。这是没有问题的，但是删除之后，虽然2删除掉了，但是多了一个3。

• 问题1解决方案：
  • 这个问题可能是因为我dequeue()方法，调用了之前父类ArrayHeap类中removeMin()方法所引起的。
  • 所以就不得不说一下我PP12.1的实现思路。实际上，队列和优先级队列一定程度上是一样的。只是CompareTo方法的判定条件不同。队列只需要将进入堆的顺序记录下来就可以然后比较即可。那么这里的调用的removeMin()方法实际上就是删除队列中顺序最低的，也就是第一个进来的元素。

  public T removeMin() throws EmptyCollectionException 
  {
      if (isEmpty())
          throw new EmptyCollectionException("ArrayHeap");
  
      T minElement = tree[0];
      tree[0] = tree[count-1];
      heapifyRemove();
      count--;
  modCount--;
      return minElement;
  }
  

  • 代码如上所示，可以发现，在把数组的最后一个赋给第一个，重排序之后呢，并没有对其进行清空操作。所以，存在会有两个3的出现。那么我只需要在之后添加一串

  tree[count] =null;
  

  就可以解决问题了。
  

代码托管

上周考试错题总结

• 
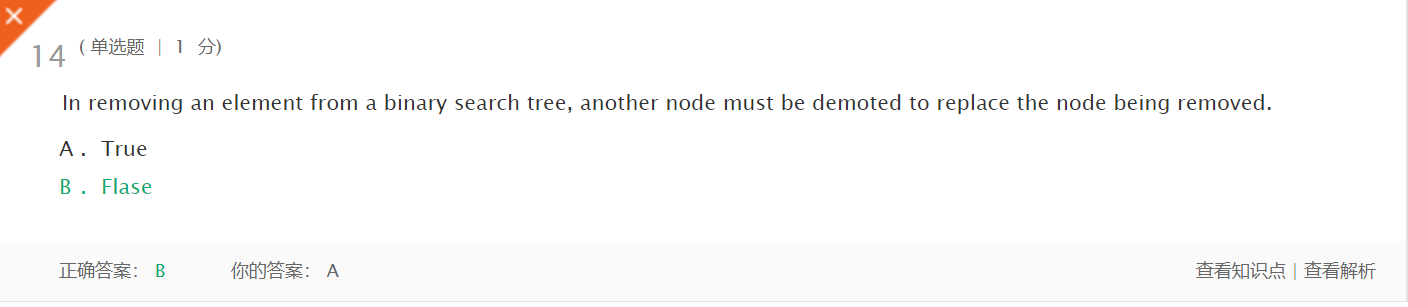
• 在二叉查找树删除结点时，如果他有孩子，那么让他的孩子代替他。应该是升级而不是降级。

结对及互评

点评过的同学博客和代码

• 上周博客互评情况
  • 20172304
  • 段志轩同学的博客是不断进步的，还是应该多多基于书本，务实基础。在代码实现方面不要急躁，耐心调试，肯定可以发现错误。
  • 20172328
  • 博客内容丰富，并且问题里讨论了上学期研究的栈内存和堆内存之间的区别。优秀。

其他

堆是基于二叉树的。这周看代码的效率并不是很高，对于代码的理解也不是很深入。归结于学习积极性不高。凡事不要钻牛角尖，过去的就过去了，一切都会好起来。不要给自己额外的压力和负担。
看过别的同学优秀的博客以后发现自己不能懈怠。比如很多同学都联系到了上学期的堆栈内存时的学习内容。学习应该有体系，不能够东拼西揍，捡西瓜丢芝麻。还是要踏实下来，戒骄戒躁。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	10/10
第二周	610/610	1/2	20/30
第三周	593/1230	1/3	18/48
第四周	2011/3241	2/5	30/78
第五周	956/4197	1/6	22/100
第六周	2294/6491	2/8	20/120
第七周	914/7405	1/9	20/140
第八周	2366/9771	2/11	22/162

参考资料

• 图解排序算法(三)之堆排序
• 堆排序原理及算法实现（最大堆）
• 排序算法（三）堆排序原理与实现（小顶堆）
• 带你体会堆算法