20172301 《Java软件结构与数据结构》实验三报告
20172301 《Java软件结构与数据结构》实验三报告
课程:《Java软件结构与数据结构》
班级: 1723
姓名: 郭恺
学号:20172301
实验教师:王志强老师
实验日期:2018年11月20日
必修/选修: 必修
一.实验内容
实验一

实验二
实验三
实验四
实验五
二.实验过程及结果
实验一:
实验一是比较简单的,代码是书上的代码。主要是Junit测试因为好久没有用过,总是会有一些错误,类似junit测试方法前没有添加test,或者junit测试的assert方法实现。
测试用例设计情况(正常,异常,边界,正序,逆序),关于测试用例,对于排序的异常,是ClassCastException,是转换发生了错误。具体是例如1、2、3、4、a、b是不可以比的,也就是不能排序。

排序应该是没有边界测试的。
对于查找的异常,是ArrayIndexOutOfBoundsException,是数组越界。即查找范围超过了数组范围。
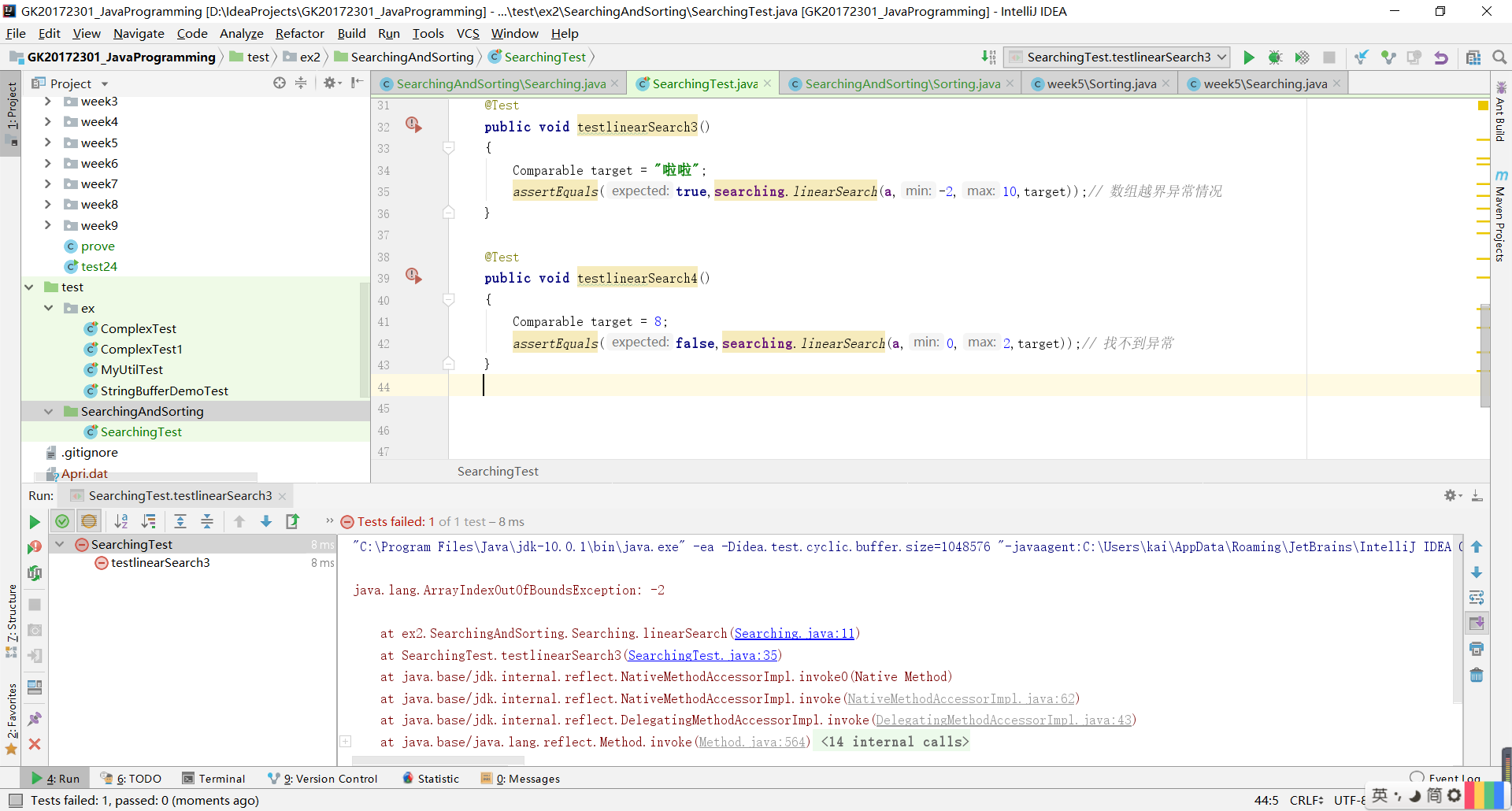
查找应该是没有逆序测试的。
-
实验一测试结果截图:
查找测试:
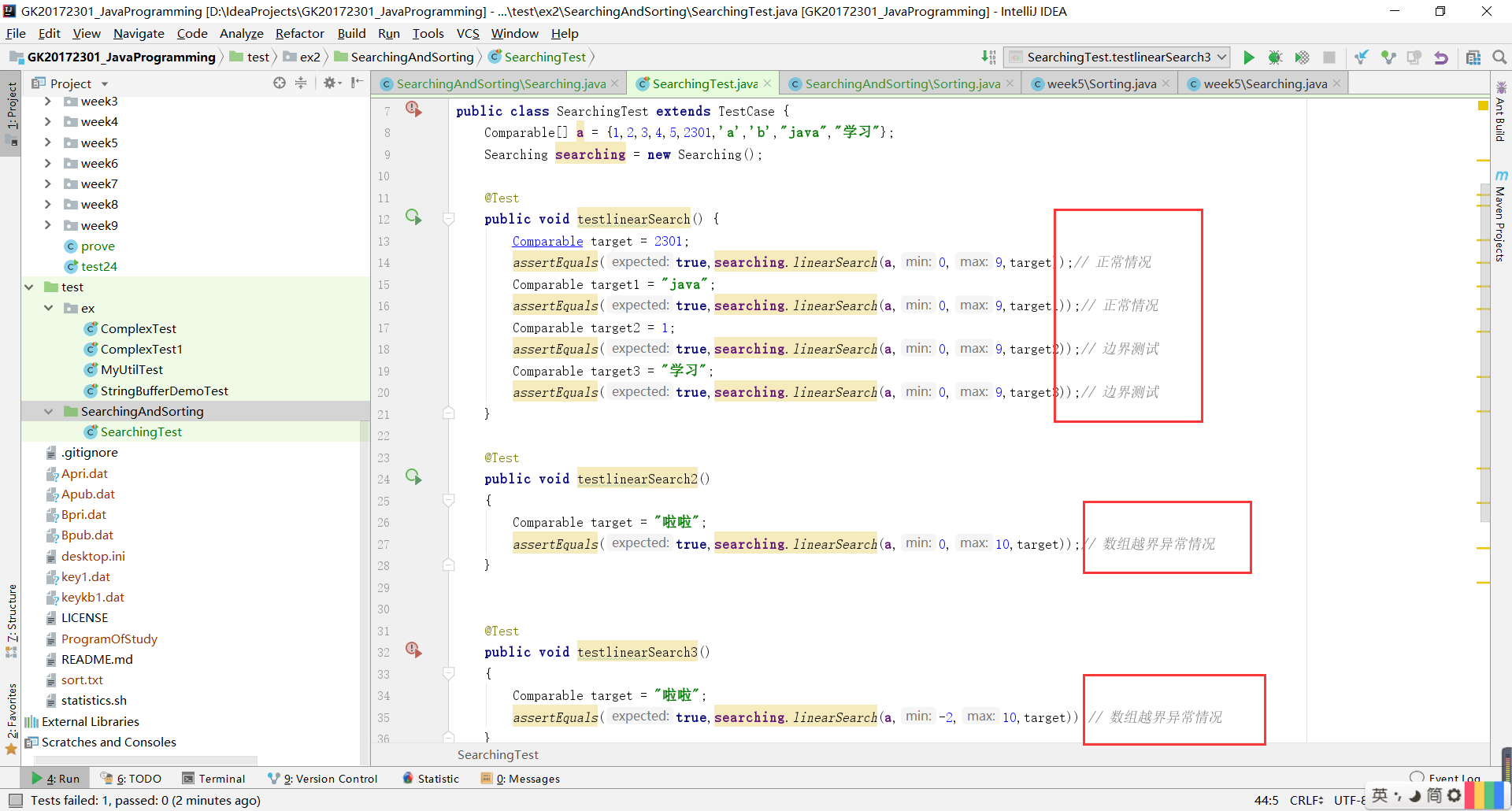
排序测试:

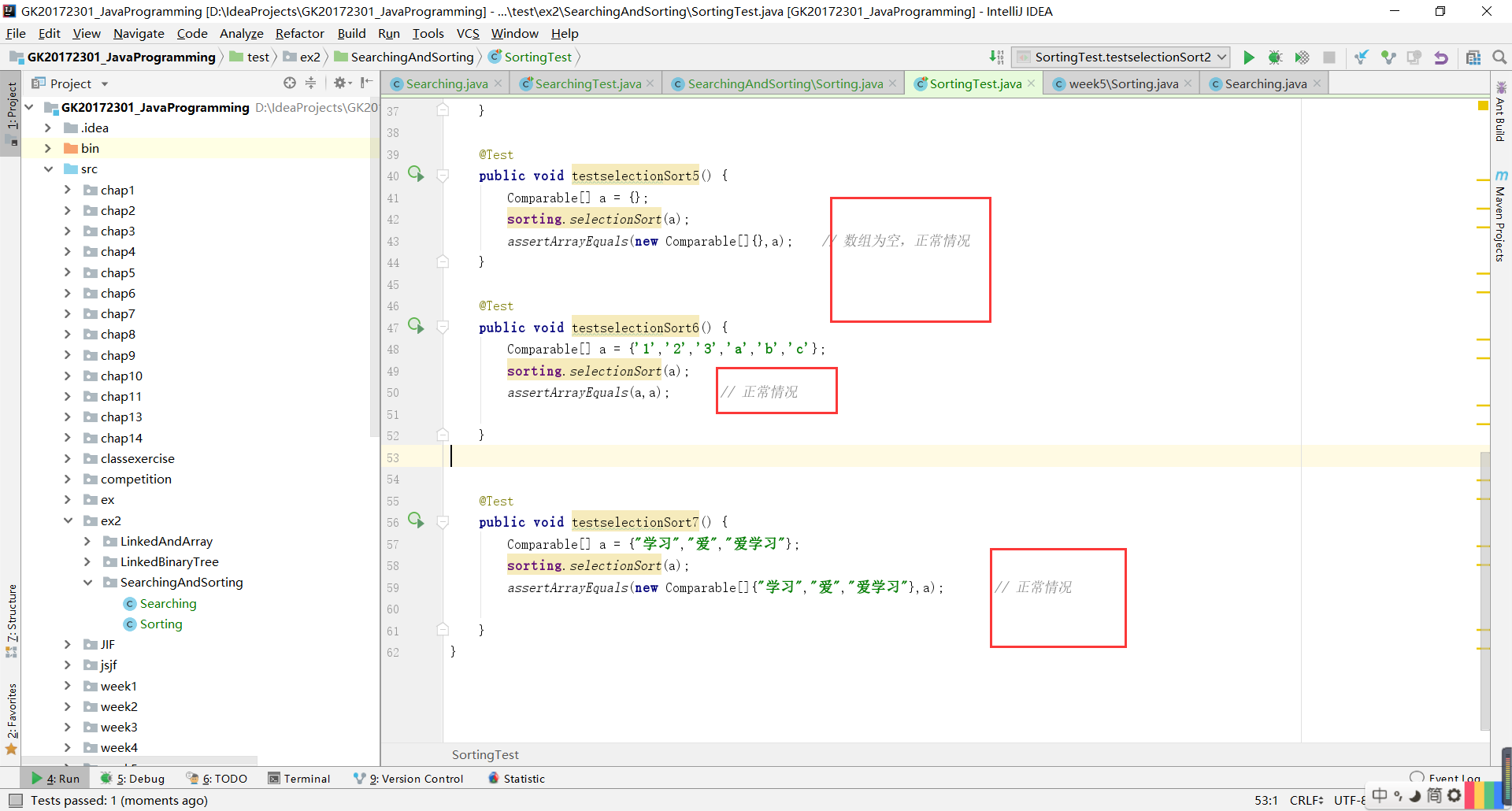
实验二:
实验二首先要移到包里面,需要注意的是测试类的位置,需要放在项目的test文件夹中,并且变更目录为Test Sources Root。
-
实验二测试结果截图:
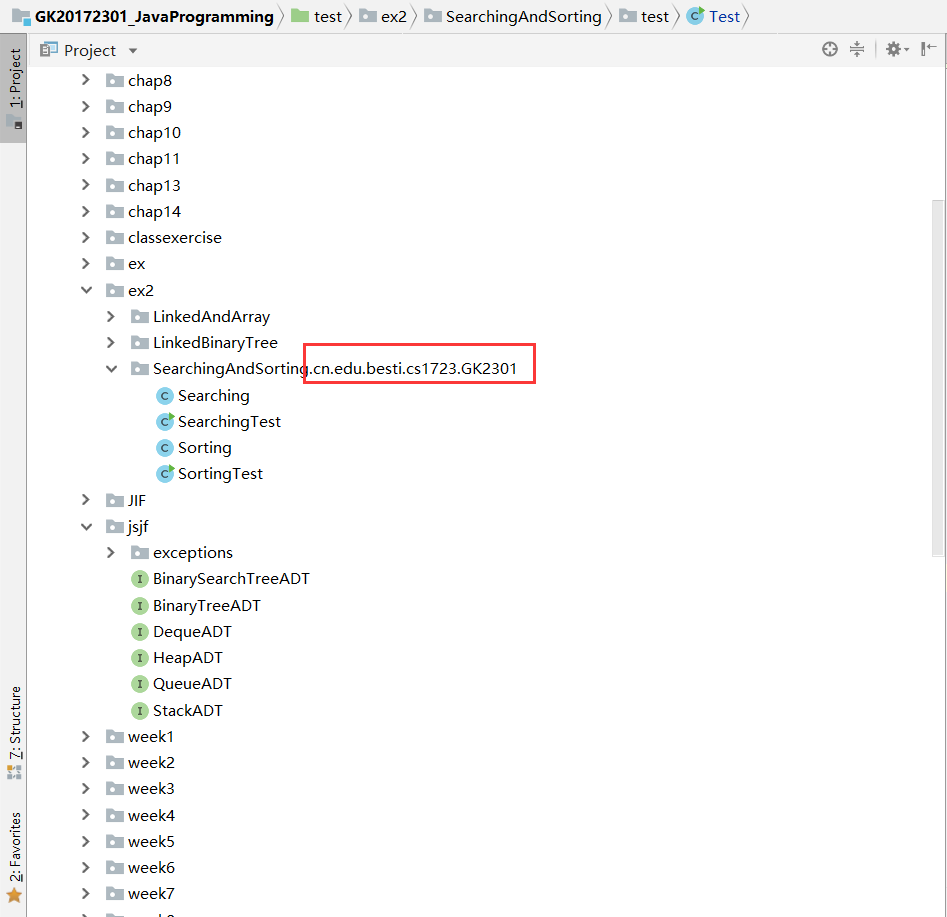
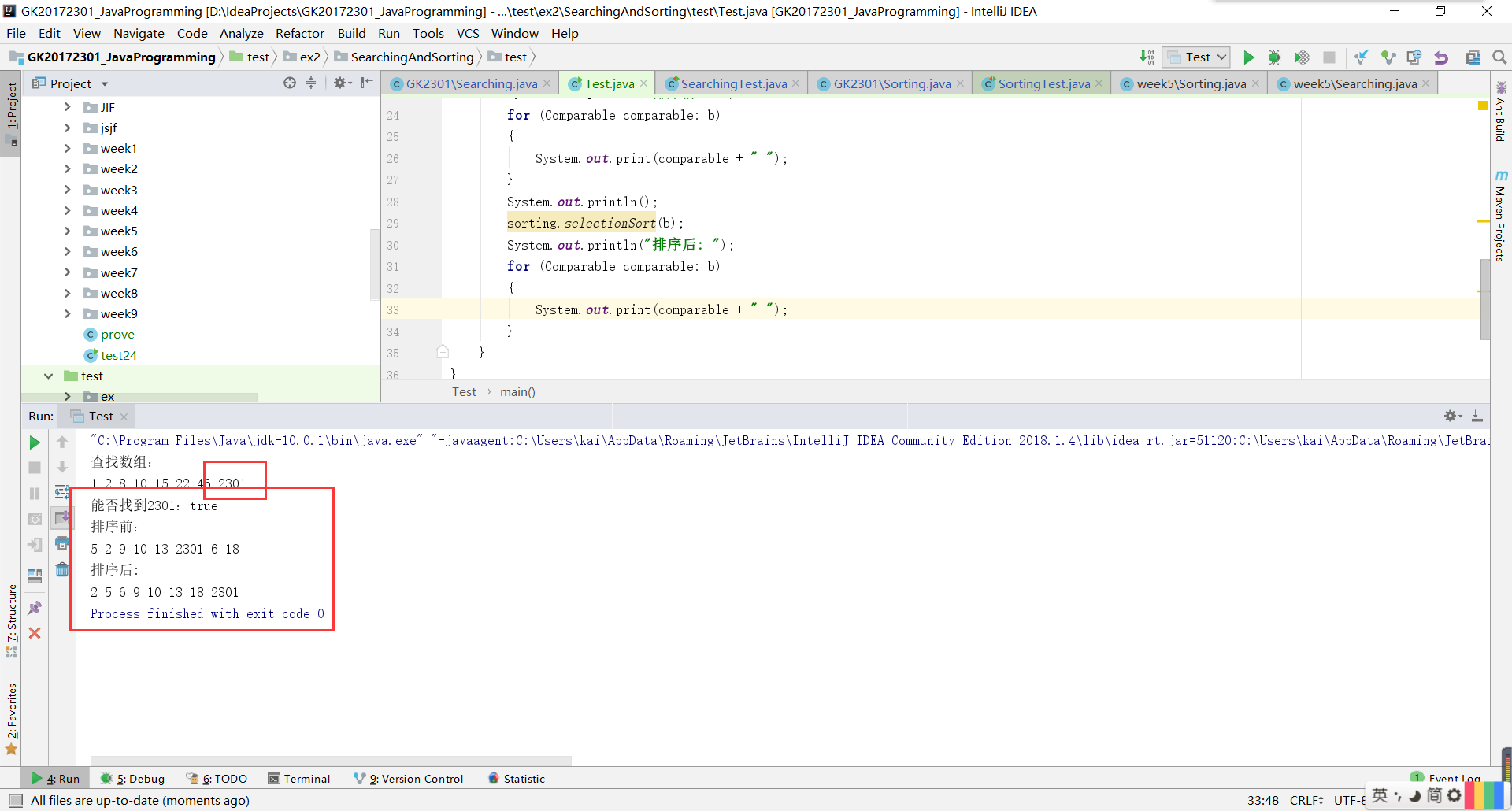

实验三:
七种查找算法分别是:线性查找、二分查找、插值查找、斐波那契查找、树表查找、分块查找、哈希查找。之前的学过的查找方式,这里就不再多说了。
需要注意的是,插值查找和斐波那契查找都是二分查找的优化,所以他们所查找的序列应该也是有序的。
我重点解释一下分块查找。
在之前的学习中,我们学习过分块排序。那么类比推理一下,分块查找的原理应该也是类似的。分块查找的最大特点就应该是块内无序,块间有序。 通过这个特点,我们可以首先可以确定目标元素在哪个块里面,然后通过顺序查找确定其位置。
可以说,是一种折半查找和顺序查找的优化改进的方法。
那么这里,我直接用了之前的分块方法。
private static <T extends Comparable<? super T>> int partition(T[] data, int min, int max)
{
T partitionelement;
int left, right;
int middle = (min + max) / 2;
//使用中间数据值作为分区元素
partitionelement = data[middle];
// 暂时把它移开
swap(data, middle, min);
left = min;
right = max;
while (left < right)
{
// 搜索一个元素,它是>分区元素
while (left < right && data[left].compareTo(partitionelement) <= 0)
left++;
// 搜索一个元素,它是<分区元素
while (data[right].compareTo(partitionelement) > 0)
right--;
// 交换元素
if (left < right)
swap(data, left, right);
}
// 将分区元素移动到适当的位置
swap(data, min, right);
return right;
}
然后,在分块查找里划分为几个部分。
int partition = partition(data,min,max);
int leftPartition = partition(data,min,partition-1);
int rightPartition = partition(data,partition+1,max);
判断具体位置后,进行线性查找。
-
实验三测试结果截图:
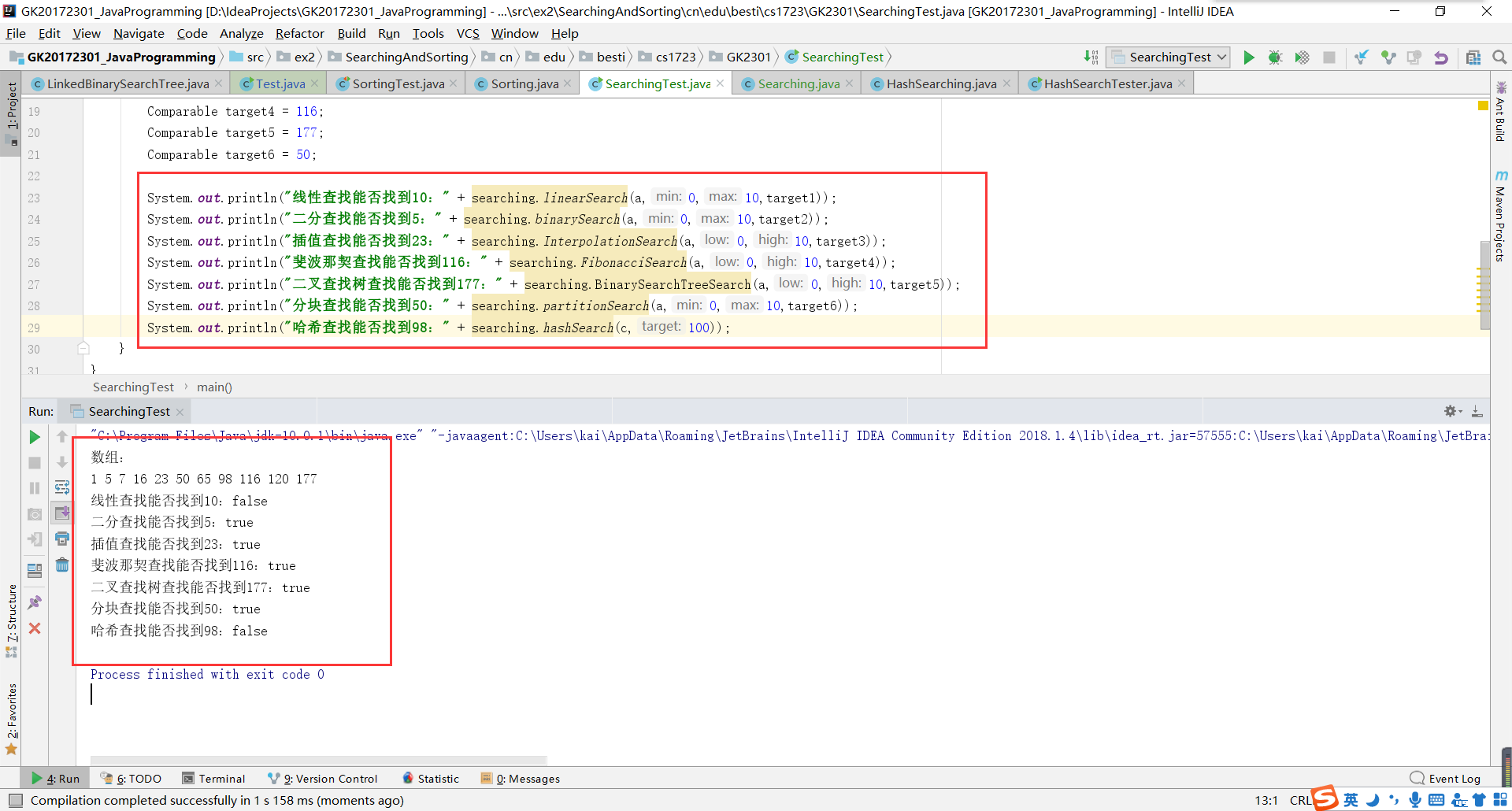
实验四:
这里的排序算法是希尔排序,堆排序,二叉树排序。
这里还是重点介绍一下希尔排序。因为有关第八周的测试,希尔排序学长提出了一点问题。
这里我先放出我当时的答案。

学长说这里应该是4插入到13的前面。

我们这里就应该注意希尔排序的基本思想:
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序也是插入排序,对简单插入排序的改进方法。
所以,对于这道题来说,最后4应该直接插入到13的前面。
-
实验四测试结果截图:
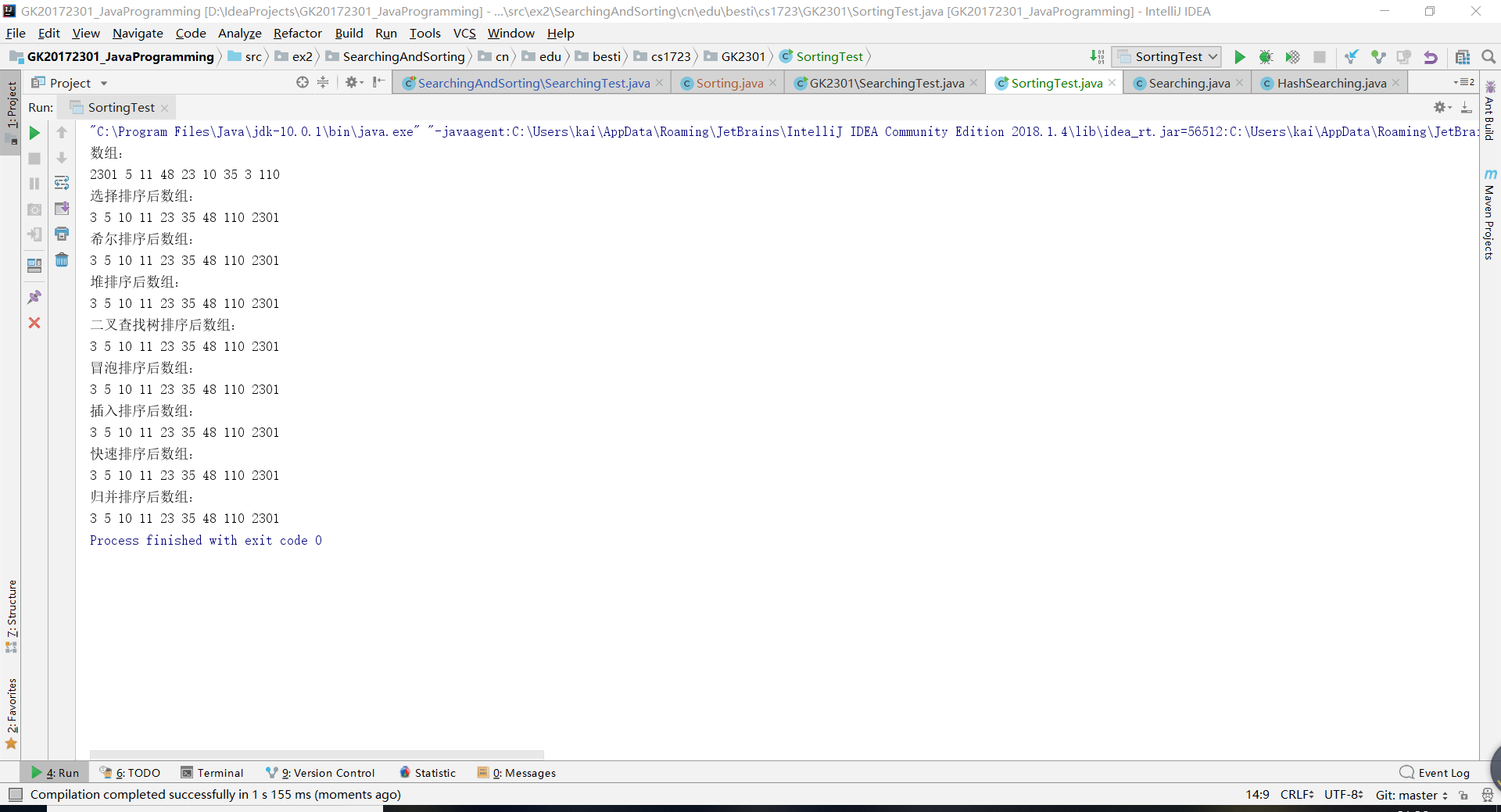
异常:
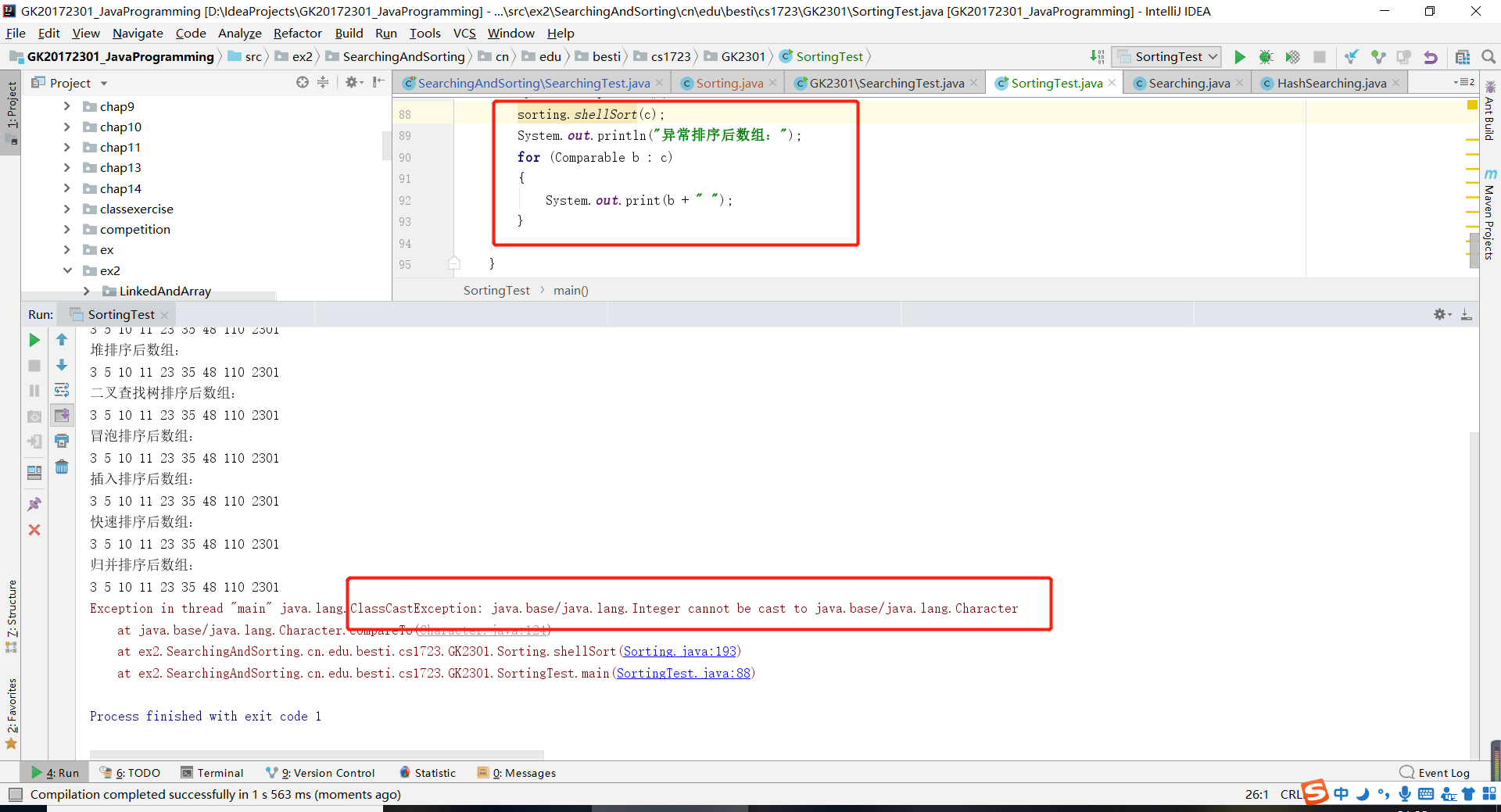
实验五:
基于安卓实现查找和排序功能。是之前实验的一个整合。
-
实验五测试结果截图:
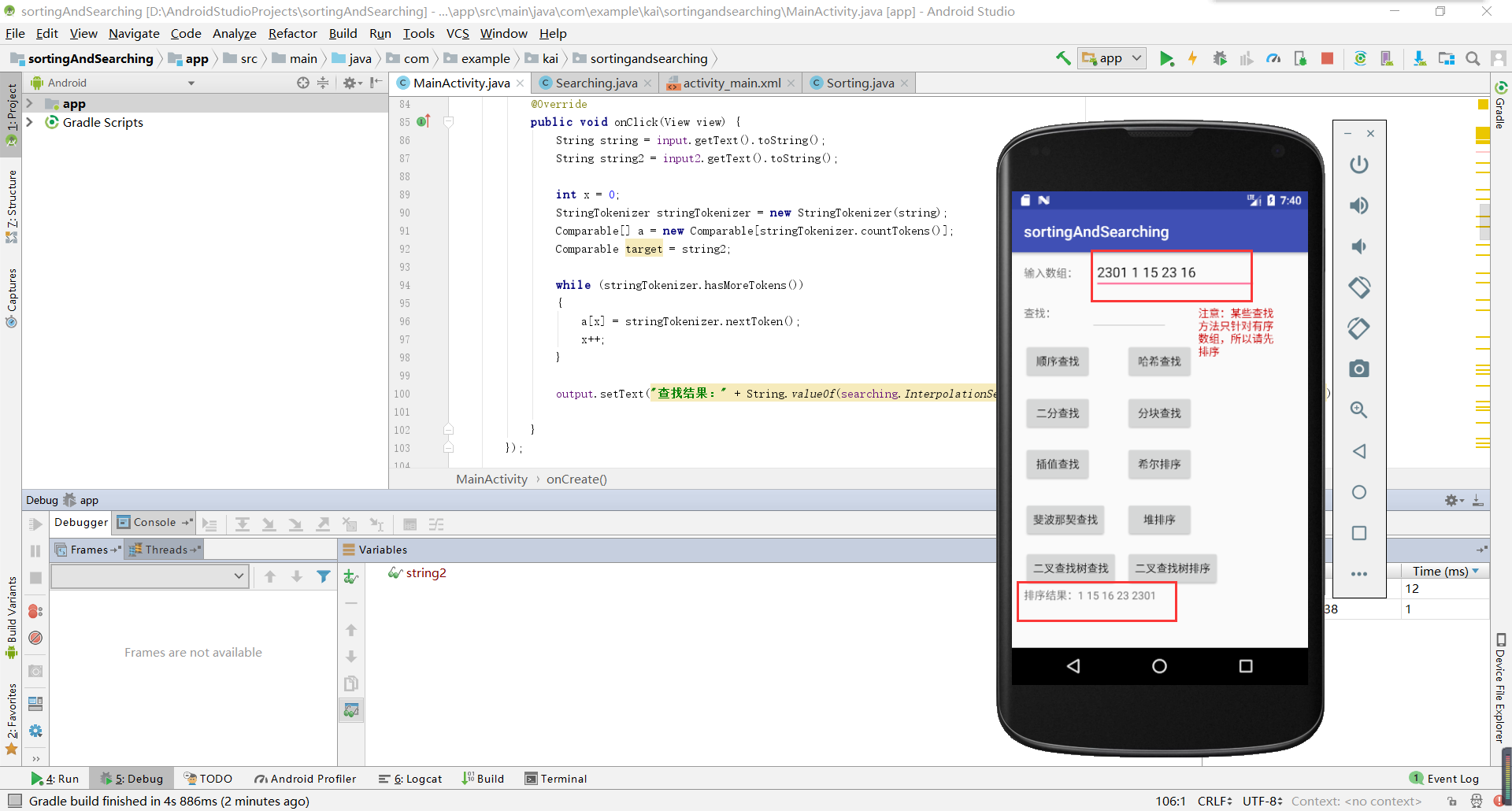
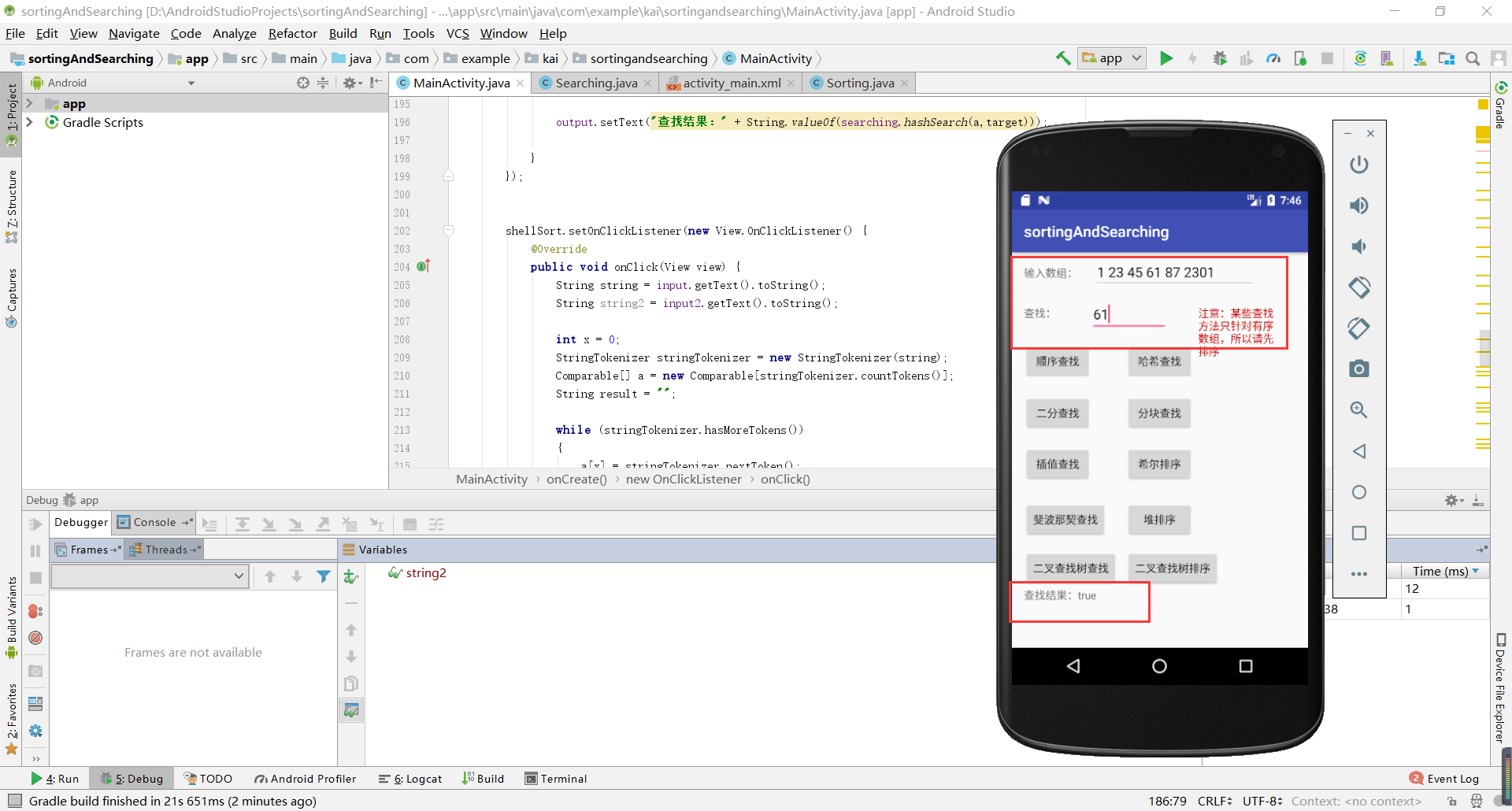
三. 实验过程中遇到的问题和解决过程
- 问题1:实验三中七种查找算法中的斐波那契查找,对于其中扩展数组的操作,C++实现:
int * temp;//将数组a扩展到F[k]-1的长度
temp=new int [F[k]-1];
memcpy(temp,a,n*sizeof(int));
int * temp是声明一个int类型的数组。
memcpy()方法应该是有关复制的操作,在java中应该如何实现。
- 问题1解决方案:
-
memcpy()函数- 函数原型:void *memcpy (void*dest, const void *src, size_t n);
- 功能:由src指向地址为起始地址的连续n个字节的数据复制到以destin指向地址为起始地址的空间内。
-
由此,这个功能应该就是复制原数组到一个新数组中。
-
在java上有多种实现方式:
- for循环代码可以说是很直观,灵活并且便于理解,但是效率有时候不高。
// 通过for循环 int[] array2 = new int[5]; for(int i = 0;i < array1.length;i++) { array2[i] = array1[i]; } for(int i = 0;i < array2.length;i++) { System.out.print(array2[i]); } System.out.println();- System.arraycopy()方法通过源码可以观察到
native,是原生态方法,效率自然更高。
public static native void arraycopy(Object src, int srcPos, Object dest, int destPos, int length);- Arrays.copyOf()方法在源码上是基于System.arraycopy(),所以效率自然低于System.arraycpoy()。
// 通过Arrays.copyOf() int[] array4 = new int[5]; array4 = Arrays.copyOf(array1, 5); for (int i = 0; i < array4.length; i++) { System.out.print(array4[i]); }- Object.clone()方法从源码来看也是native方法,但返回为Object类型,所以赋值时将发生强转,所以效率不如之前两种。
// 通过Object.clone() int[] array5 = new int[5]; array5 = array4.clone(); for (int i = 0; i < array5.length; i++) { System.out.print(array5[i]); }
-
其他(感悟、思考等)
- 这周做完实验没有及时总结,因为时间比较久远,导致有一些错误和解决方法都有所遗忘。部分参考资料还是在浏览器的历史记录中淘到的。以后要对错误及时总结,养成良好的学习习惯。



