根据一个数组，创建一个Segment Tree(线段树)

一、线段树的特点

1.没有度为1的结点，只有度为0和2的结点
2.线段树的叶子结点对应于数组中的一个元素
3.线段树是一种静态结构，即可以进行查询和更新操作，但是不能进行插入和删除操作
4.线段树和对应的数组相比，求i~j号元素之间所有元素的和，最小值，最大值等，具有较高的查询和更新效率（O(logn) VS O(n)）

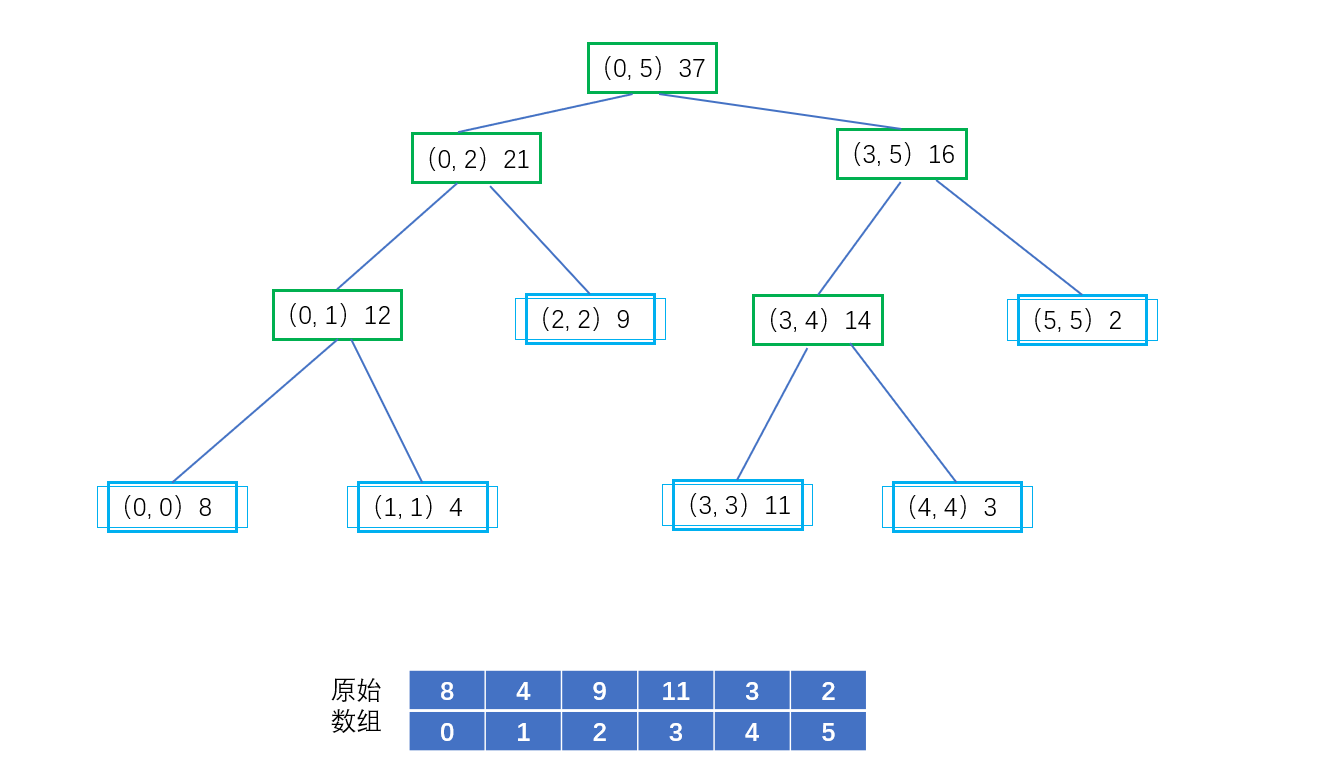
二、线段树的构造过程

（0，5）37：数组元素下标0~5的元素之和是37
（0，2）21：数组元素下标0~2的元素之和是21

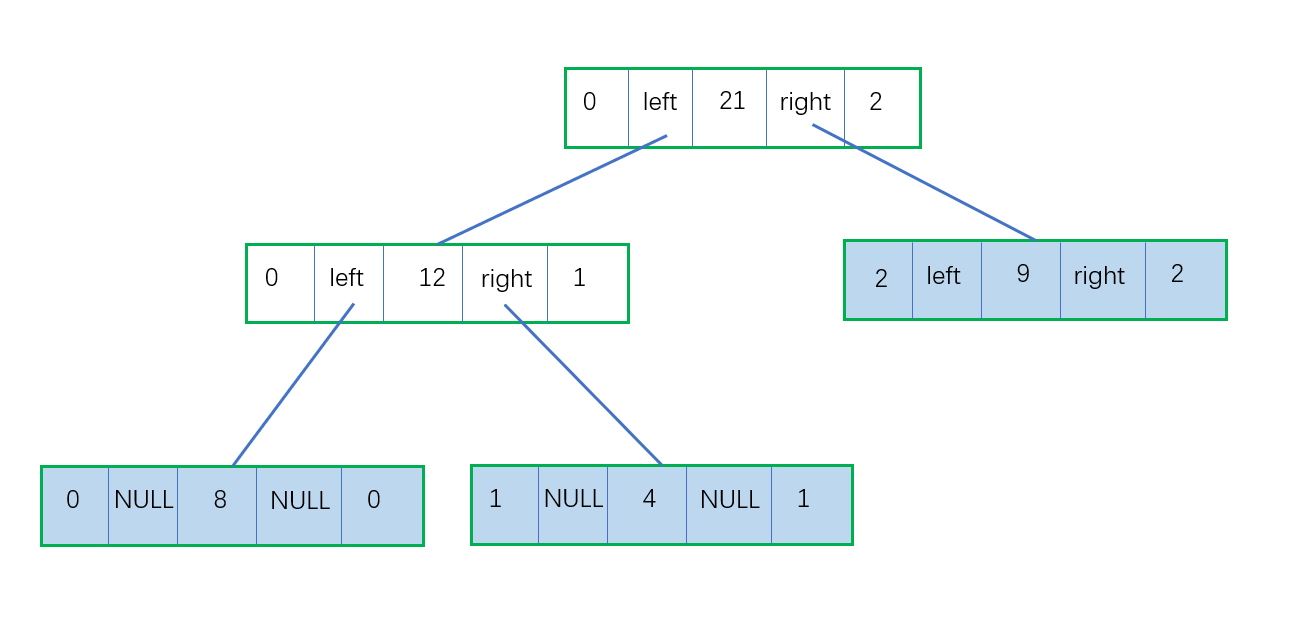
三、线段树的基本数据结构（结点结构由五个分量组成）

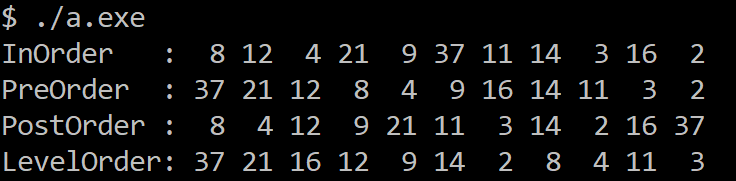
四、遍历线段树的运行结果

五、基于线段树的查询操作：给定两个索引i,j查询i~j之间所有元素的和

讨论查询效率：如果使用数组查询i~j之间所有元素的和，(最坏)时间复杂度是O(n)，而是用线段树的最坏时间复杂度是O(log(n))，遥遥领先！

int search(SegmentTree T, int i, int j) {
	int ret = 0;
	int l = T->lidx, r = T->ridx;
	if (i == l && j == r) {
		/*这是最特殊的情况，也是递归函数的出口*/
		ret = T->sum;
	} else if(i <= (l+r)/2 && j <= (l+r)/2) {
		ret = search(T->left, i, j);	
	} else if(i > (l+r)/2 && j >= (l+r)/2) {
		/*正确分段很重要!*/
		ret = search(T->right, i, j);	
	} else if(i <= (l+r)/2 && j>= (l+r)/2) {
		ret = search(T->left, i, (l+r)/2) + search(T->right, (l+r)/2 + 1, j);	
	}
 
	return ret;
}

六、基于线段树的更新操作：给定一个索引i和值value，更新对应结点叶子节点的值，并且更新该叶子结点到根结点路径上所有结点的值

讨论查询效率：使用数组更新索引i的值为value，时间复杂度为O(1)，而是用线段树的时间复杂度是O(log(n)), 更新效率数组更高！
讨论查询效率：使用数组更新i~j区间所有的值，时间复杂度为O(n)，而是用线段树的时间复杂度是O(log(n)), 更新效率线段树更高！

/*仅仅更新的是某一个索引idx的值，尚未实现更新idx~jdx区间所有的值*/
void update(SegmentTree T, int idx, int value) {
	if (idx == T->lidx && idx == T->ridx) {
		/*递归出口*/		
		T->sum = value;
	} else if (idx <= (T->lidx + T->ridx)/2) {
		update(T->left, idx, value);
		T->sum = T->left->sum + T->right->sum;
	} else {
		update(T->right, idx, value);
		T->sum = T->left->sum + T->right->sum;
	}
}

七、完整的C代码。基于一个数组，创建一颗线段树

1. 先序、中序、后序遍历线段树
2. 利用队列FIFO的特性，层序遍历线段树
3. 仅遍历线段树的叶子结点
4. 基于创建好的线段树，进行查询和更新操作
5. 求出线段树的树高

点击查看代码

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
 
typedef struct TNode{
	/*线段树的结点结构*/
	int lidx, ridx;
	struct TNode *left, *right;
	int sum;
} TNode, *SegmentTree;
 
typedef struct QNode{
	/*队列的结点结构，队列用于层序遍历线段树*/
	TNode* ptr2TNode;
	struct QNode *next;
} QNode, *Queue;
 
SegmentTree build(int* arr, int l, int r);
void inOrder(SegmentTree T);
void preOrder(SegmentTree T);
void postOrder(SegmentTree T);
void levelOrder(SegmentTree T, Queue queue);
void visit(TNode* Node);
Queue initQueue();
TNode* delete(Queue queue);
void add(Queue queue, TNode* Node);
bool isEmpty(Queue queue);
void leafOnly(SegmentTree T);
int search(SegmentTree T, int i, int j);
void update(SegmentTree T, int i, int value);
int height(SegmentTree T);
 
int main(int argc, char* argv[]) {
	int arr[] = {8, 4, 9, 11, 3, 2};
	/*创建线段树*/
	SegmentTree SegTree = build(arr, 0, sizeof(arr)/sizeof(int) - 1);
	
	/*中序遍历线段树*/
	printf("InOrder   : ");
	inOrder(SegTree);
	printf("\n");
 
	/*先序遍历线段树*/
	printf("PreOrder  : ");
	preOrder(SegTree);
	printf("\n");
 
	/*后序遍历线段树*/
	printf("PostOrder : ");
	postOrder(SegTree);
	printf("\n");
 
	/*层序遍历线段树*/
	printf("LevelOrder: ");
	Queue queue = initQueue();
	levelOrder(SegTree, queue);
 
	/*打印数组钟的原始数据*/
	printf("\nidx : ");
	for (int i = 0; i < sizeof(arr)/sizeof(int); i++) {
		printf("%2d ", i);
	}
	printf("\ndata: ");
	for (int i = 0; i < sizeof(arr)/sizeof(int); i++) {
		printf("%2d ", arr[i]);
	}
	/*根据创建好的线段树进行查询操作*/
	printf("\n");
	printf("%d~%d sum is: %d\n", 0, 1, search(SegTree, 0, 1)); 
	printf("%d~%d sum is: %d\n", 1, 1, search(SegTree, 1, 1)); 
	printf("%d~%d sum is: %d\n", 0, 2, search(SegTree, 0, 2)); 
	printf("%d~%d sum is: %d\n", 2, 2, search(SegTree, 2, 2)); 
	printf("%d~%d sum is: %d\n", 0, 3, search(SegTree, 0, 3)); 
	printf("%d~%d sum is: %d\n", 1, 4, search(SegTree, 1, 4)); 
	printf("%d~%d sum is: %d\n", 2, 5, search(SegTree, 2, 5)); 
	printf("%d~%d sum is: %d\n", 3, 4, search(SegTree, 3, 4)); 
	printf("%d~%d sum is: %d\n", 4, 4, search(SegTree, 4, 4)); 
	printf("%d~%d sum is: %d\n", 3, 5, search(SegTree, 3, 5)); 
	printf("%d~%d sum is: %d\n", 5, 5, search(SegTree, 5, 5)); 
 
	/*基于线段树，进行更新操作*/
	leafOnly(SegTree);
	printf("\n");
	update(SegTree, 3, 20);
	update(SegTree, 2, 11);
	leafOnly(SegTree);
	printf("\n");

	/*求出线段树的高度*/
	printf("Height of SegTree = %d\n", height(SegTree));
 
	return 0;
}
 
SegmentTree build(int* arr, int l, int r) {
    /*创建一颗线段树*/
	TNode* T = (TNode*)malloc(sizeof(TNode));
	T->lidx = l, T->ridx = r;
    /*叶子节点的left和right指针都是空
      叶子结点的sum域对应于数组的元素
      非叶子节点的left和right指针需要递归创建
      非叶子节点的sum域等于左右孩子的sum域之和
    */
	if (l < r) {
		T->left = build(arr, l, (l+r)/2);
		T->right = build(arr, (l+r)/2 + 1, r);
		T->sum = T->left->sum + T->right->sum;
	} else if(l == r) {
		T->left = NULL, T->right = NULL;
		T->sum = arr[l];
	}
	return T;
}
 
void inOrder(SegmentTree T) {
    /*中序遍历线段树*/
	if (T != NULL) {
		inOrder(T->left);
		visit(T);
		inOrder(T->right);
	}
}
 
void visit(TNode* Node) {
    /*访问线段树的结点（对线段树的结点进行读写）*/
	printf("%2d ", Node->sum);
}
 
void preOrder(SegmentTree T) {
    /*先序遍历线段树*/
	if (T != NULL) {
		visit(T);
		preOrder(T->left);
		preOrder(T->right);
	}
}

void postOrder(SegmentTree T) {
    /*后序遍历线段树*/
	if (T != NULL) {
		postOrder(T->left);
		postOrder(T->right);
		visit(T);
	}	
}
 
Queue initQueue() {
    /*初始化一个空队列*/
	Queue q = (Queue)malloc(sizeof(QNode));
	q->ptr2TNode = NULL;
	q->next = NULL;
	return q;
}
 
TNode* delete(Queue queue) {
    /*队头元素出队*/
	if (!isEmpty(queue)) {
		QNode* temp = queue->next;
		queue->next = temp->next;		
		TNode* ret = temp->ptr2TNode;
		free(temp);
		return ret;
	}
	return NULL;
}
 
void add(Queue queue, TNode* Node) {
    /*元素在队尾入队*/
	QNode* temp = queue;
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	newnode->ptr2TNode = Node;
	newnode->next = NULL;
	while (temp->next != NULL) {
		temp = temp->next;
	}
	temp->next = newnode;
}

bool isEmpty(Queue queue) {
	/*判断队列是否为空*/
	return queue->next == NULL;
}

void levelOrder(SegmentTree T, Queue queue) {
    /*层序遍历线段树*/
	add(queue, T);
	while (!isEmpty(queue)) {
		TNode* node = delete(queue);
		visit(node);
		if (node->left != NULL) add(queue, node->left);
		if (node->right !=NULL) add(queue, node->right);
	}
}

int search(SegmentTree T, int i, int j) {
    /*求出i~j之间所有元素的和*/
	int ret = 0;
	int l = T->lidx, r = T->ridx;
	if (i == l && j == r) {
		/*递归函数的出口*/
		ret = T->sum;
	} else if(i <= (l+r)/2 && j <= (l+r)/2) {
		ret = search(T->left, i, j);	
	} else if(i > (l+r)/2 && j >= (l+r)/2) {
		/*正确分段很重要!*/
		ret = search(T->right, i, j);	
	} else if(i <= (l+r)/2 && j>= (l+r)/2) {
		ret = search(T->left, i, (l+r)/2) + search(T->right, (l+r)/2 + 1, j);	
	}
 
	return ret;
}
 
void update(SegmentTree T, int idx, int value) {
	if (idx == T->lidx && idx == T->ridx) {
		/*递归出口（首先找到idx对应的叶子结点）*/		
		T->sum = value;
	} else if (idx <= (T->lidx + T->ridx)/2) {
		update(T->left, idx, value);
		T->sum = T->left->sum + T->right->sum;
	} else {
		update(T->right, idx, value);
		T->sum = T->left->sum + T->right->sum;
	}
}
 
void leafOnly(SegmentTree T) {
	/*遍历线段树，但是只遍历叶子结点*/
	if (T != NULL) {
		if (T->left == NULL) {
			visit(T);
		}
		leafOnly(T->left);
		leafOnly(T->right);
	}
}
 
int height(SegmentTree T) {
	int h = 0;
	if (T != NULL) {
		/*用小括号把三元表达式括起来*/
		h = 1 + ((height(T->left) > height(T->right)) ? height(T->left) : height(T->right));
	}
	return h;
}