图解算法——跳台阶/爬楼梯

 

1、题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/climbing-stairs
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2、示例

示例1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

3、解题思路

第一次看到这道题，可能会有点不知所措。但是不要着急，我们可以暴力，我们可以穷举！

思路1：

当 n = 1时，一共跳 1 级；

当 n = 2时，一共跳 2 级；

当 n = 3时，一共跳 3 级；

当 n = 4时，一共跳 5 级；

当 n = 5时，一共跳 8 级；

...

咦？这不就是去了第一个项的斐波那契数列嘛？

到此为止，我们可以列出方程了：f(n) = f(n-1) + f(n-2);

不过，我们需要手动增加  0 项为 1 。

所以，代码如下：

class Solution {
    public int climbStairs(int n) {
        if(n==1 || n==0){
            return 1;
        }     
        return climbStairs(n-1)+climbStairs(n-2);
    }
}

提交结果：

 

 

 思路2：

第二个思路是，利用动态规划。其实，这个题目也是动态规划的经典题目。

本问题其实常规解法可以分成多个子问题，爬第n阶楼梯的方法数量，等于以下两部分之和：

• 爬上 n-1 阶楼梯的方法数量：因为再爬1阶就能到第 n 阶；
• 爬上 n-2 阶楼梯的方法数量：因为再爬2阶就能到第 n 阶。

所以我们得到公式 dp[n] = dp[n-1] + dp[n-2]；
同时需要初始化 dp[0]=1 和 dp[1]=1；
时间复杂度：O(n)。

代码如下：

class Solution {
    public int climbStairs(int n) {
        if(n==1 || n==0){
            return 1;
        }
        int[] arr = new int[n+1];
        arr[0] = 1;
        arr[1] = 1;
        for(int i = 2; i<n+1; i++){
            arr[i] = arr[i-1] + arr[i-2];
        }
        return arr[n];
    }
}

提交结果如下：

 

 

 思路3：

是的，这道题还有第三种方法。

那就是纯数学方法，有人说上面不也是数学方法嘛？是的，上面也是，但是下面这个更厉害。

由第一种方法我们可知是斐波那契数列，其实菲波那切数列是有公式的。

 

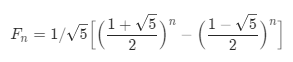
 时间复杂度为：O(log n)。

代码如下：

class Solution {
    public int climbStairs(int n) {
        double sqrt_5 = Math.sqrt(5);
        double fib_n = Math.pow((1 + sqrt_5) / 2, n + 1) - Math.pow((1 - sqrt_5) / 2,n + 1);
        return (int)(fib_n / sqrt_5);
    }
}

提交结果和第二种差不多。

 OK ，下一篇我们来看跳台阶的进阶版。

 

 

Over......