图解算法——购物单
1、题目描述
王强今天很开心,公司发给N元的年终奖。王强决定把年终奖用于购物,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子:
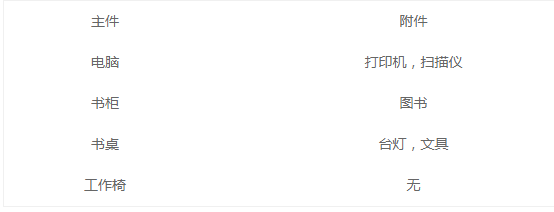
如果要买归类为附件的物品,必须先买该附件所属的主件。每个主件可以有 0 个、 1 个或 2 个附件。附件不再有从属于自己的附件。王强想买的东西很多,为了不超出预算,他把每件物品规定了一个重要度,分为 5 等:用整数 1 ~ 5 表示,第 5 等最重要。他还从因特网上查到了每件物品的价格(都是 10 元的整数倍)。他希望在不超过 N 元(可以等于 N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第 j 件物品的价格为 v[j] ,重要度为 w[j] ,共选中了 k 件物品,编号依次为 j 1 , j 2 ,……, j k ,则所求的总和为:
v[j 1 ]*w[j 1 ]+v[j 2 ]*w[j 2 ]+ … +v[j k ]*w[j k ] 。(其中 * 为乘号)
请你帮助王强设计一个满足要求的购物单。
题目来源:https://www.nowcoder.com/practice/f9c6f980eeec43ef85be20755ddbeaf4?tpId=37&tags=&title=&difficulty=0&judgeStatus=0&rp=1
2、示例
输入描述:
输入的第 1 行,为两个正整数,用一个空格隔开:N m
(其中 N ( <32000 )表示总钱数, m ( <60 )为希望购买物品的个数。)
从第 2 行到第 m+1 行,第 j 行给出了编号为 j-1 的物品的基本数据,每行有 3 个非负整数 v p q
(其中 v 表示该物品的价格( v<10000 ), p 表示该物品的重要度( 1 ~ 5 ), q 表示该物品是主件还是附件。如果 q=0 ,表示该物品为主件,如果 q>0 ,表示该物品为附件, q 是所属主件的编号)
输出描述:
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值( <200000 )。
示例1
输入:
1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0
输出:
2200
3、解题思路
看到这道题,第一感觉就是有点像 0-1背包问题,是的,只不过有点变形而已,相比0-1背包问题的两个约束条件(价值和容量),这里有三个约束条件(价值,权重,主附件),而且最后一种约束条件还比较特殊(主附件)。
所以我们确定:该题是背包问题的变种,我们需要套用背包问题的解法,只需要改动状态转移方程。
背包问题中状态转移方程为F(i, j) =max(F(i - 1, j),F(i - 1, j - w) + value),其中j >= w,否则F(i, j) = F(i - 1, j)。这题的核心变化,就是后面新增的物品i可能是前面物品i - k的附件,购买附件就必须先买主件,所以得要考虑前面已经得到的最优解中是否已经购买过了该主件。
那么,怎样解决此主件是否被购买的问题?那就是把附件考虑到主件中,当后面新增一个物品i,该物品是附件时,直接令F(i, j) = F(i - 1, j),相当于跳过附件i。
把附件考虑到主件的方法:
当遇到一个物品i,其是主件时(PS:题目规定,每个主件可以有0个、1个或2个附件),那么,具体购买有以下四种购买情况:
(1)仅仅购买主件
(2)购买主件和附件1
(3)购买主件和附件2
(4)购买主件和附件1和附件2
代码如下:
import java.util.Scanner; public class Main { static class good { //物品内部类 public int v; //物品的价格 public int p; //物品的重要度 public int q; public int a1 = 0; //附件1的编号 public int a2 = 0; //附件2的编号 good(int v, int p, int q) { this.v = v; this.p = p; this.q = q; } public void setA1(int a1) { this.a1 = a1; } public void setA2(int a2) { this.a2 = a2; } } public int getMax(int a, int b) { return a > b ? a : b; } public void printResult(int N, good[] A) { int[][] dp = new int[A.length][N + 1]; for(int i = 1, len = A.length;i < len;i++) { int v = -1, v1 = -1, v2 = -1, v3 = -1, tempDp = -1, tempDp1 = -1, tempDp2 = -1, tempDp3 = -1; v = A[i].v; tempDp = v * A[i].p; if(A[i].a1 != 0) { //主件+附件1 v1 = v + A[A[i].a1].v; tempDp1 = tempDp + A[A[i].a1].v * A[A[i].a1].p; } if(A[i].a2 != 0){ //主件+附件2 v2 = v + A[A[i].a2].v; tempDp2 = tempDp + A[A[i].a2].v * A[A[i].a2].p; } if(A[i].a1 != 0 && A[i].a2 != 0) { //主件+附件1+附件2 v3 = v + A[A[i].a1].v + A[A[i].a2].v; tempDp3 = tempDp + A[A[i].a1].v * A[A[i].a1].p + A[A[i].a2].v * A[A[i].a2].p; } for(int j = 1;j <= N;j++) { if(A[i].q > 0) { //当物品i是附件时,相当于跳过 dp[i][j] = dp[i - 1][j]; } else { dp[i][j] = dp[i - 1][j]; if(j >= v && v != -1) dp[i][j] = getMax(dp[i - 1][j], dp[i - 1][j - v] + tempDp); if(j >= v1 && v1 != -1) dp[i][j] = getMax(dp[i - 1][j], dp[i - 1][j - v1] + tempDp1); if(j >= v2 && v2 != -1) dp[i][j] = getMax(dp[i - 1][j], dp[i - 1][j - v2] + tempDp2); if(j >= v3 && v3 != -1) dp[i][j] = getMax(dp[i - 1][j], dp[i - 1][j - v3] + tempDp3); } } } System.out.println(dp[A.length - 1][N]); return; } public static void main(String[] args) { Main test = new Main(); Scanner in = new Scanner(System.in); int N = in.nextInt(); int m = in.nextInt(); if(m <= 0) { System.out.println(0); return; } good[] A = new good[m + 1]; int v, p, q; for(int i = 1;i <= m;i++) { v = in.nextInt(); p = in.nextInt(); q = in.nextInt(); A[i] = new good(v, p, q); if(q > 0) { if(A[q].a1 == 0) A[q].setA1(i); else A[q].setA2(i); } } test.printResult(N, A); } }
提交运行时间:

参考并致谢:
1、https://www.cnblogs.com/liuzhen1995/p/6590009.html
Over......




