图解算法——矩阵转换（Rotate Image）

1. 题目描述

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

英文不好的同学不要慌，请接着看例子：

2. Examples

示例1：

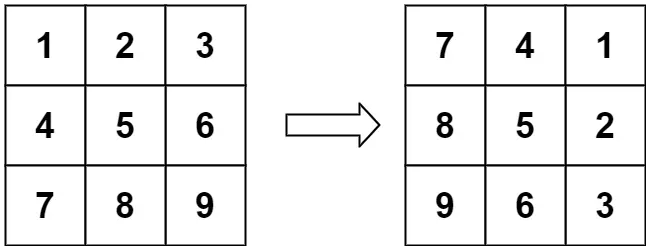
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

示例2：

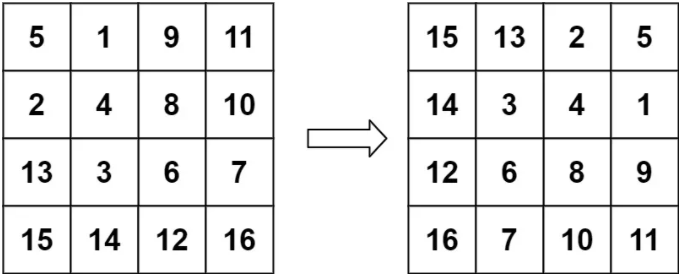
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例3：

Input: nums = [1]
Output: [[1]]

示例4：

Input: matrix = [[1,2],[3,4]]
Output: [[3,1],[4,2]]

要求：

• matrix.length == n；
• matrix[i].length == n；
• 1 <= n <= 20；
• -1000 <= matrix[i][j] <= 1000；
• 不得再占用另外空间，即要求在原矩阵上直接变换，不能再创建新的矩阵。

 

3、题目分析

从输入可以看出，矩阵是方阵即行列数相等。

故有两种思路：

 【第一种】

是记录左上角和右下角的坐标，一层一层往里，循环交换，类似这样：

 

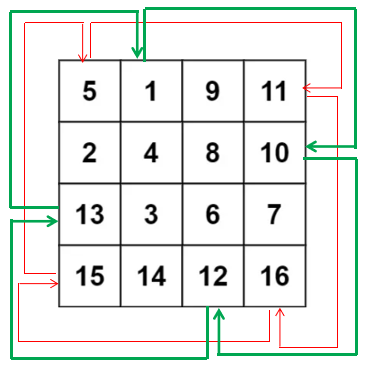
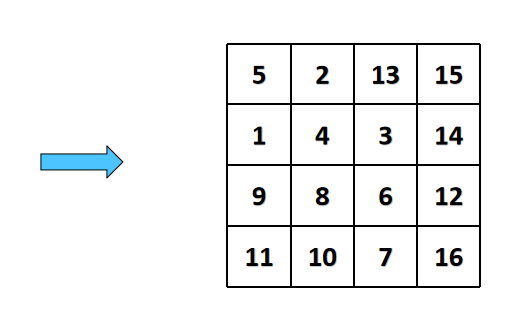
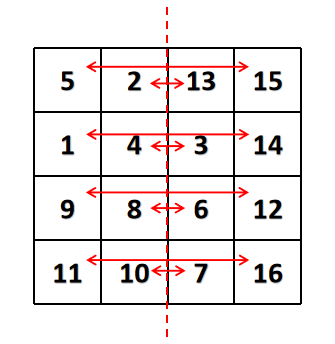
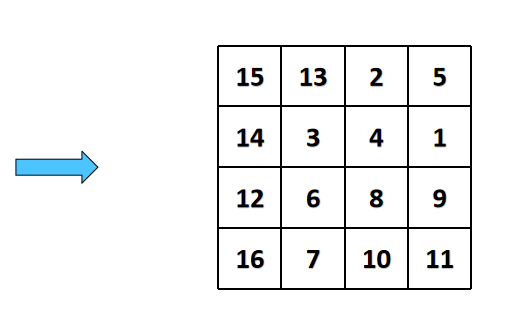
 【第二种】

是先上下三角置换，再左右水平置换，类似于这样：

第一步：

    

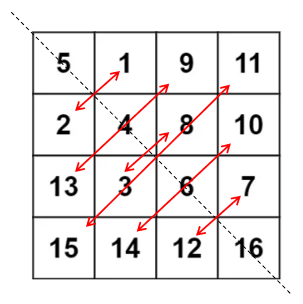
第二步：

       

第二种再举一个例子吧：

// 三行三列：
 1 2 3     1 4 7     7 4 1
 4 5 6  => 2 5 8  => 8 5 2
 7 8 9     3 6 9     9 6 3
//四行四列
5   1   9  11        5  2   13 15      15 13  2  5
2   4   8  10    =>  1  4   3  14  =>  14  3  4  1
13  3   6   7        9  8   6  12      12  6  8  9
15  14 12  16        11 10  7  16      16  7 10 11

 

4、代码实现

 

class Solution{
    ////思路一：转圈依次交换
    public void rotateImage(int[][] matrix){
        int i = 0;
        int leftTop = 0;
        int rightDown = matrix.length-1;
        int temp=0;
        while(leftTop<rightDown){
            for(i=0; i<rightDown-leftTop; i++){
                temp = matrix[leftTop][leftTop+i];
                matrix[leftTop][i] = matrix[rightDown-i][leftTop];
                matrix[rightDown-i][leftTop] = matrix[rightDown][rightDown-i];
                matrixmatrix[rightDown][rightDown-i] = matrix[rightDown][leftTop+i];
                matrix[rightDown][leftTop+i] = temp;
            }
            leftTop++;
            rightDown--;
        }
        
    }
    ////思路二：这个思路比较新，是进行转置+交换，该思路简单易操作。
    public void rotateImage1(int[][] matrix){
        int row = matrix.length;
        int col = matrix[0].length;
        
        for(int i = 0; i<row; i++){
            for(int j = 0; j<i; j++){//第i行只需要处理前i-1个元素
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        for(int i = 0; i<row; i++){
            for(int j = 0; j<col/2; j++){//第i行只需要处理前col/2个元素
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][col-j-1];
                matrix[i][col-j-1] = temp;
            }
        }
        
    }
}

 

Over......